Overview of Statistical Learning (and Competition Overview)

Dr. Gilbert

January 6, 2026

Comment: Confirmatory versus Exploratory Workflows

There are two different circumstances from which we can come at statistics and data projects.

• Exploratory Settings: Where we don’t yet have well-defined expectations or formal hypotheses generated about associations, patterns, or relationships in our data.

  • The data itself will, at least in part, dictate the direction of our analyses.

• Confirmatory Settings: Where we have generated formal hypotheses or perhaps even officially pre-registered them prior to collecting any data.

The scenario we are in dictates the workflow we must use in order to conduct valid inference.

Exploratory Settings and Workflows

In MAT300, we’ll often be working with data from contexts in which we don’t have deep subject-matter expertise.

Because of this, we’ll take an initial exploratory stance when working with our data.

• We’ll use exploratory data analysis (EDA) to uncover patterns, associations, and relationships that may exist in the data.
• We’ll use what we learn from that EDA to inform our modeling choices.

Generating hypotheses and then testing those hypotheses on the same observations compromises the validity of inference (see: snooping, fishing, p-hacking, etc.).

For this reason, in our course, we’ll split our data into a training (exploratory) set and at least one validation set.

We’ll conduct exploratory data analyses, generate hypotheses, and train models on the training data.

We’ll assess the performance of those models on the validation set(s).

Confirmatory Settings and Workflows

It is also common to approach a statistics/data problem with pre-generated or pre-registered hypotheses.

These hypotheses are declared prior to any data collection and are justified by theory, prior experience, or justifiable expectations.

In these cases, the training and validation set approach is not necessary.

The investigator can simply proceed with modeling, model assessment, and interpretation using all of the available data.

They may not, however, change their hypotheses or adjust their model after fitting and analysing the one corresponding to their initial hypotheses and still treat the resulting inference as confirmatory.

Sometimes Splitting is Still Necessary: If model predictions are going to be used to inform decision-making, then data splitting is still necessary, even in the confirmatory setting. This is because predictive performance metrics generated from the data the model was trained on will be overly optimistic.

Important Takeaway Point: While we take an exploratory approach in MAT300, all of the model construction, model assessment (particularly significance testing), and model interpretation techniques we learn apply directly in confirmatory settings as well.

Statistical Learning in Pictures

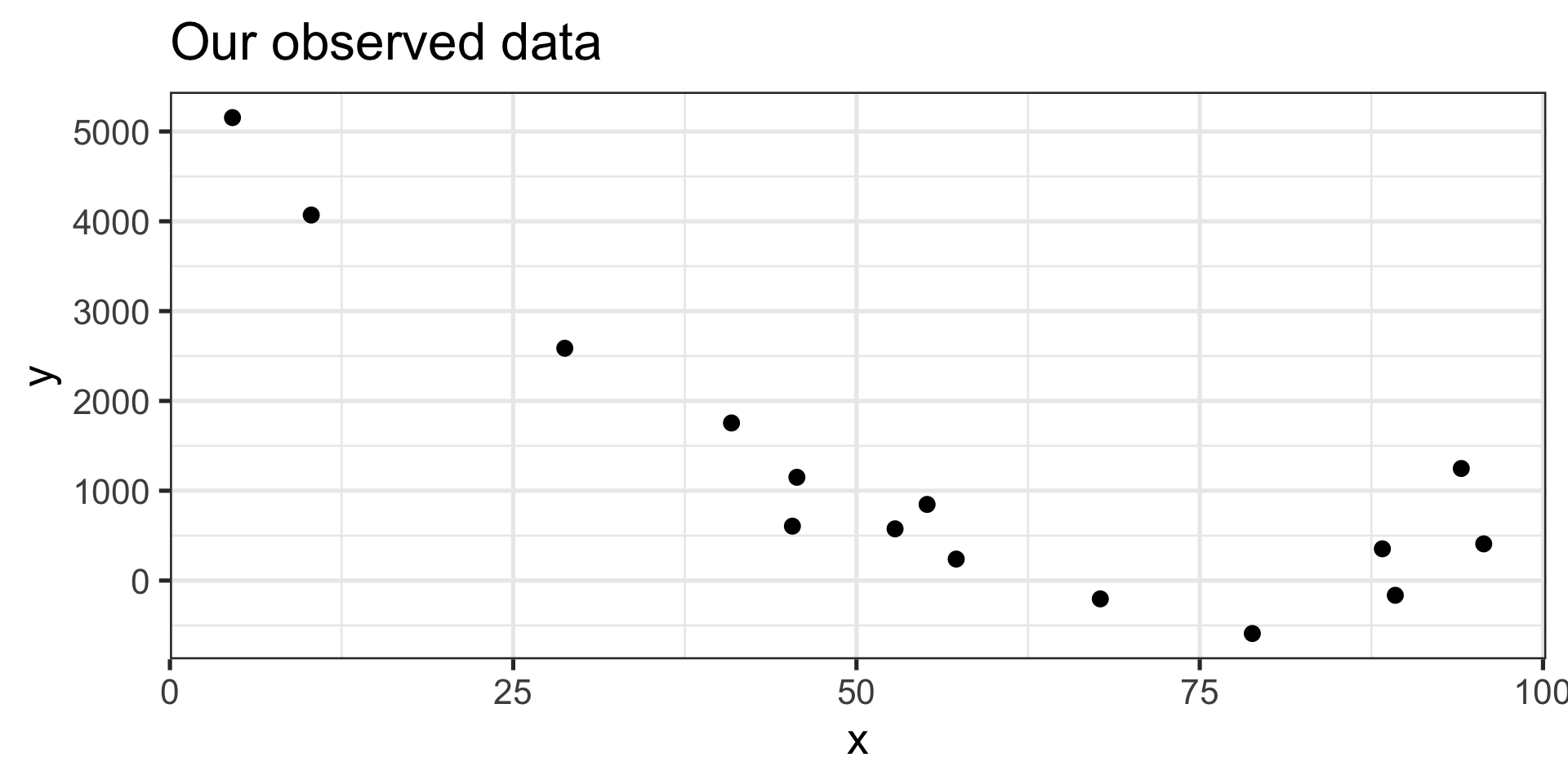
Statistical Learning in Pictures

• Goal: Build a model \(\displaystyle{\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x}\) to predict \(y\), given \(x\).

• Generalized Goal: Build a model \(\displaystyle{\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k}\) to predict \(y\) given features \(x_1, \cdots, x_k\).

  • \(\beta_i\)’s are parameters, learned from training data.

Statistical Learning in Pictures

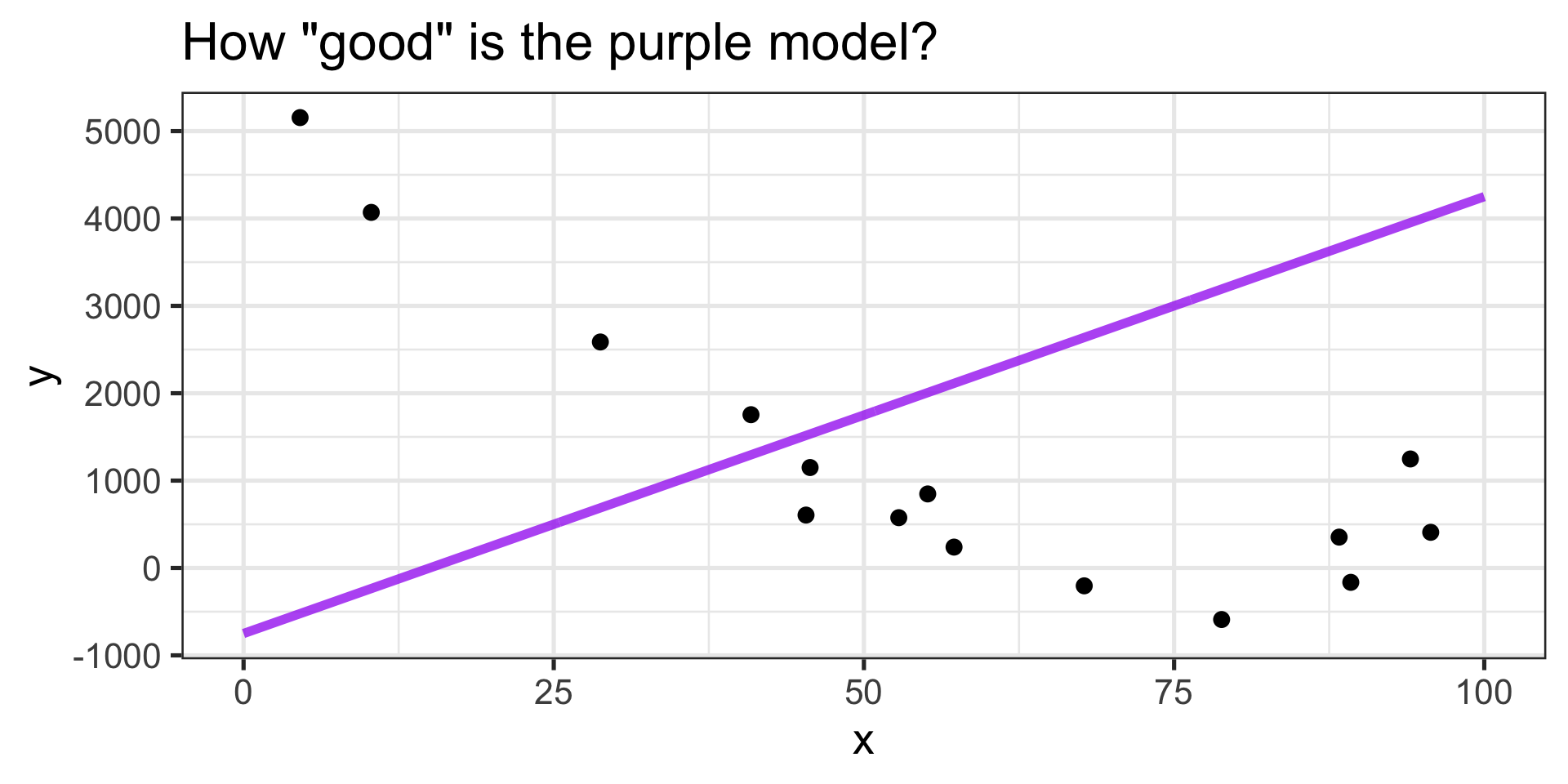
• This model doesn’t capture the general trend between our observed \(x\) and \(y\) pairs.

Statistical Learning in Pictures

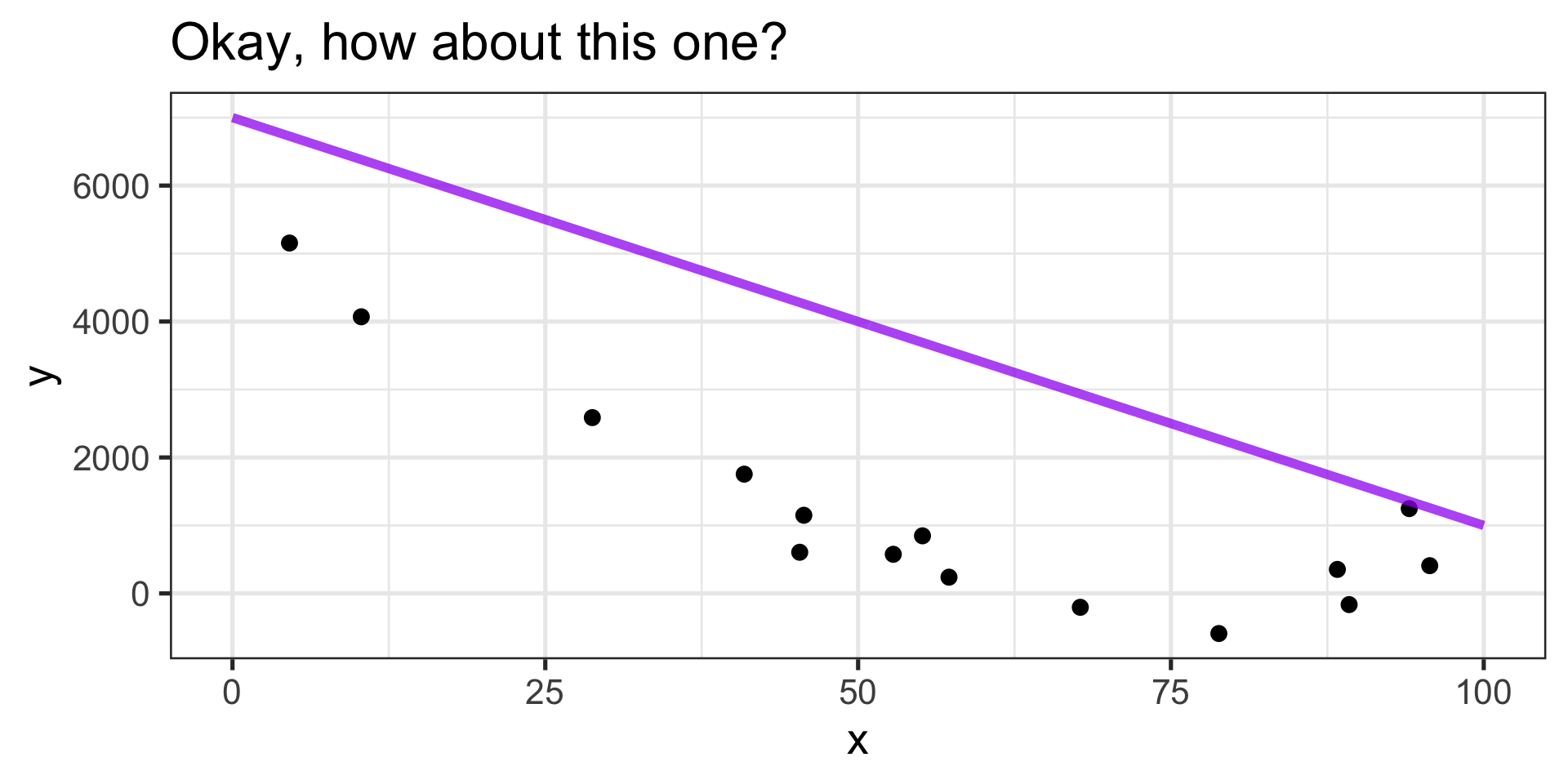
• Better job capturing the general trend (sort of).
• Larger \(x\) values are associated with smaller \(y\) values.

Statistical Learning in Pictures

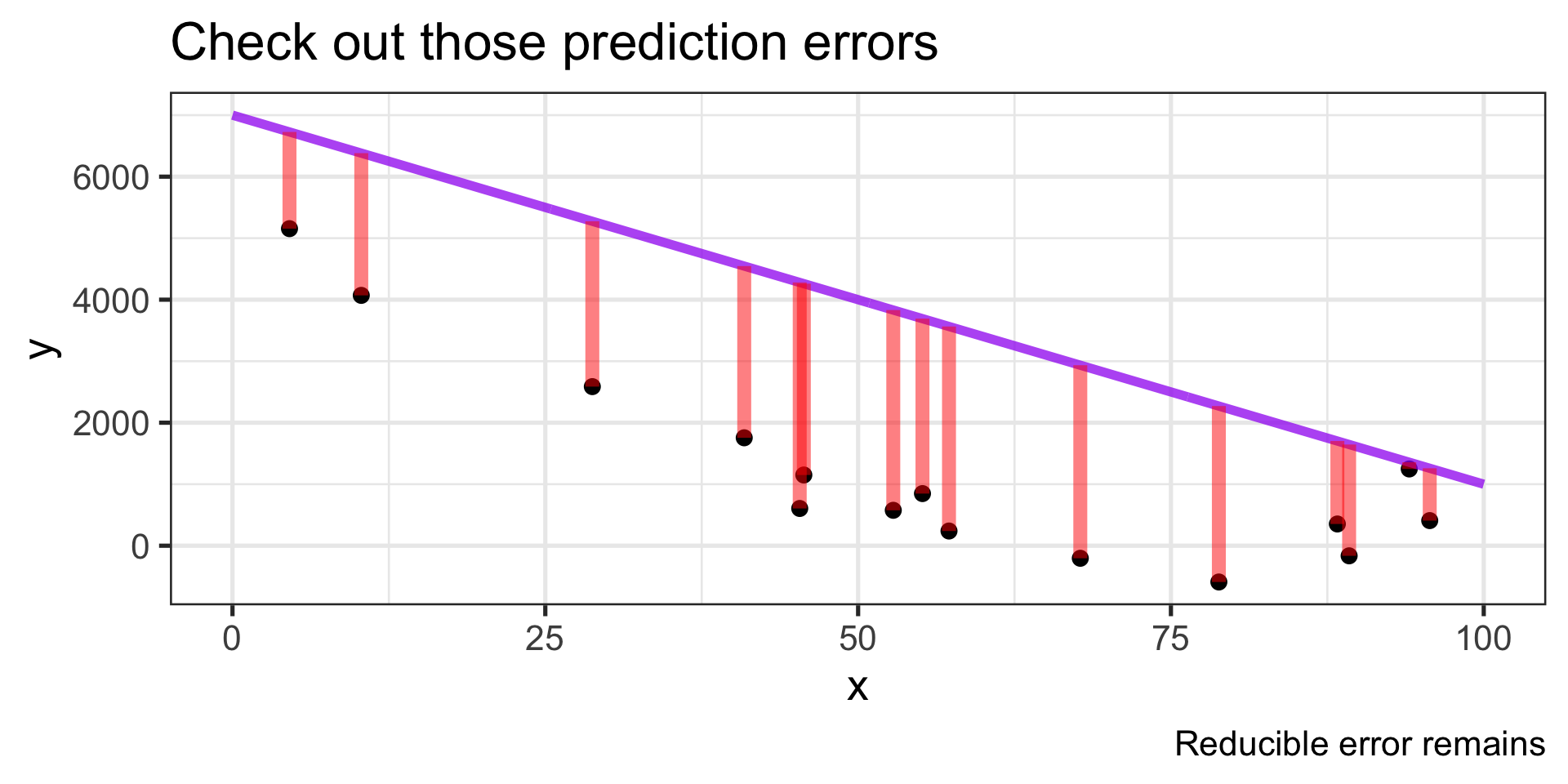
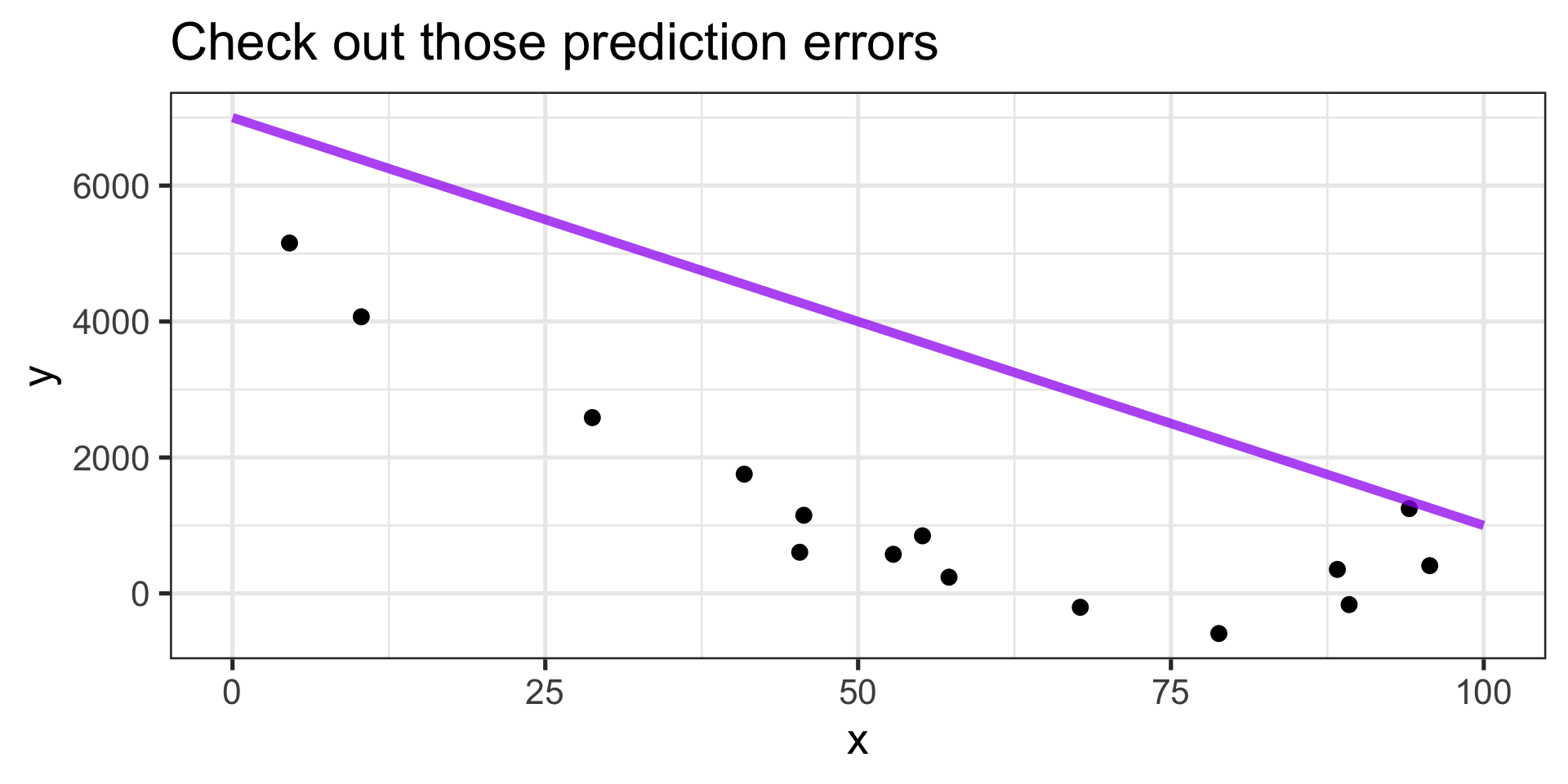
Statistical Learning in Pictures

• Always predicting too high!

  • We should overpredict sometimes and underpredict others. The average error should be \(0\).

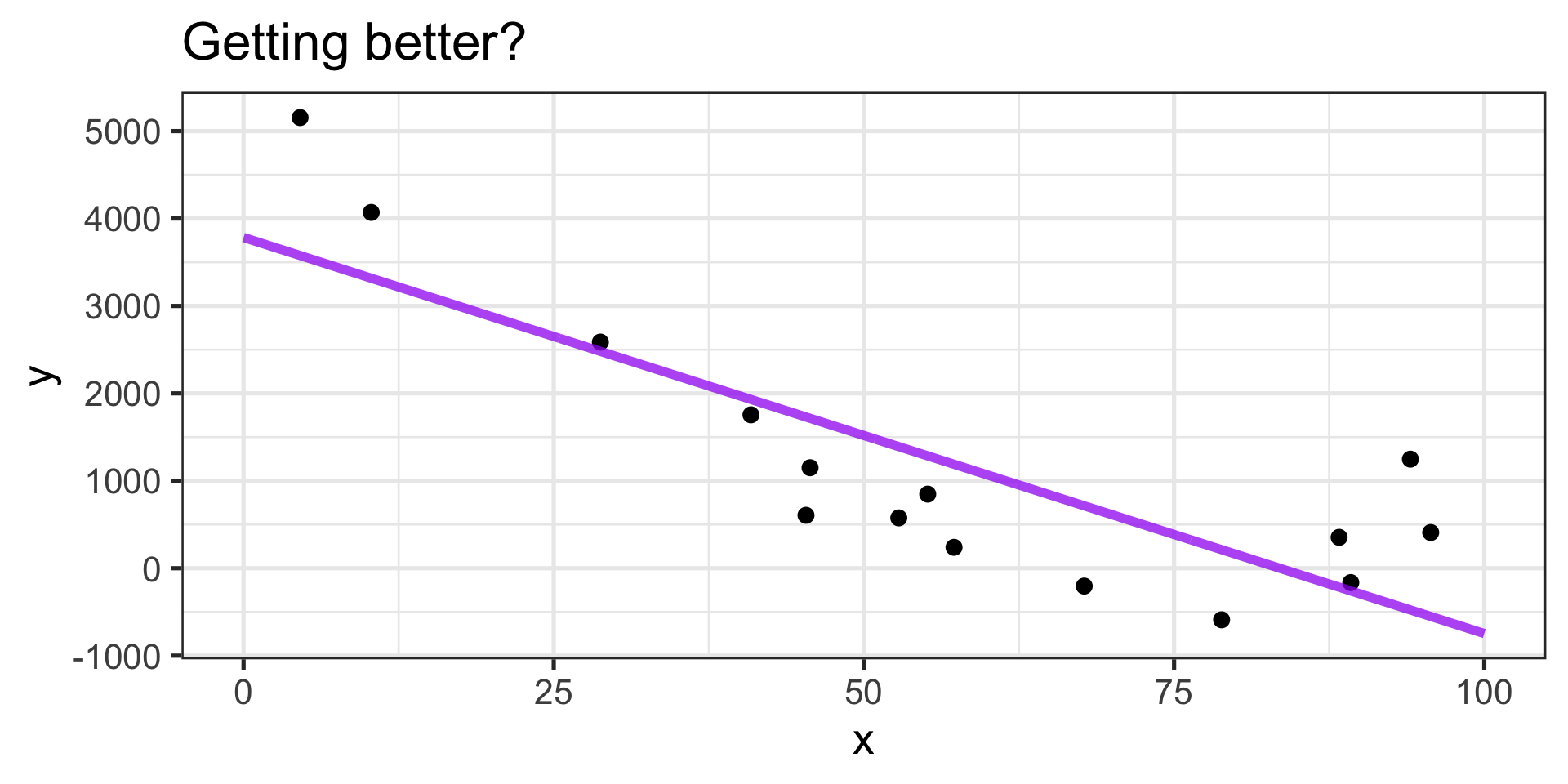
Statistical Learning in Pictures

Statistical Learning in Pictures

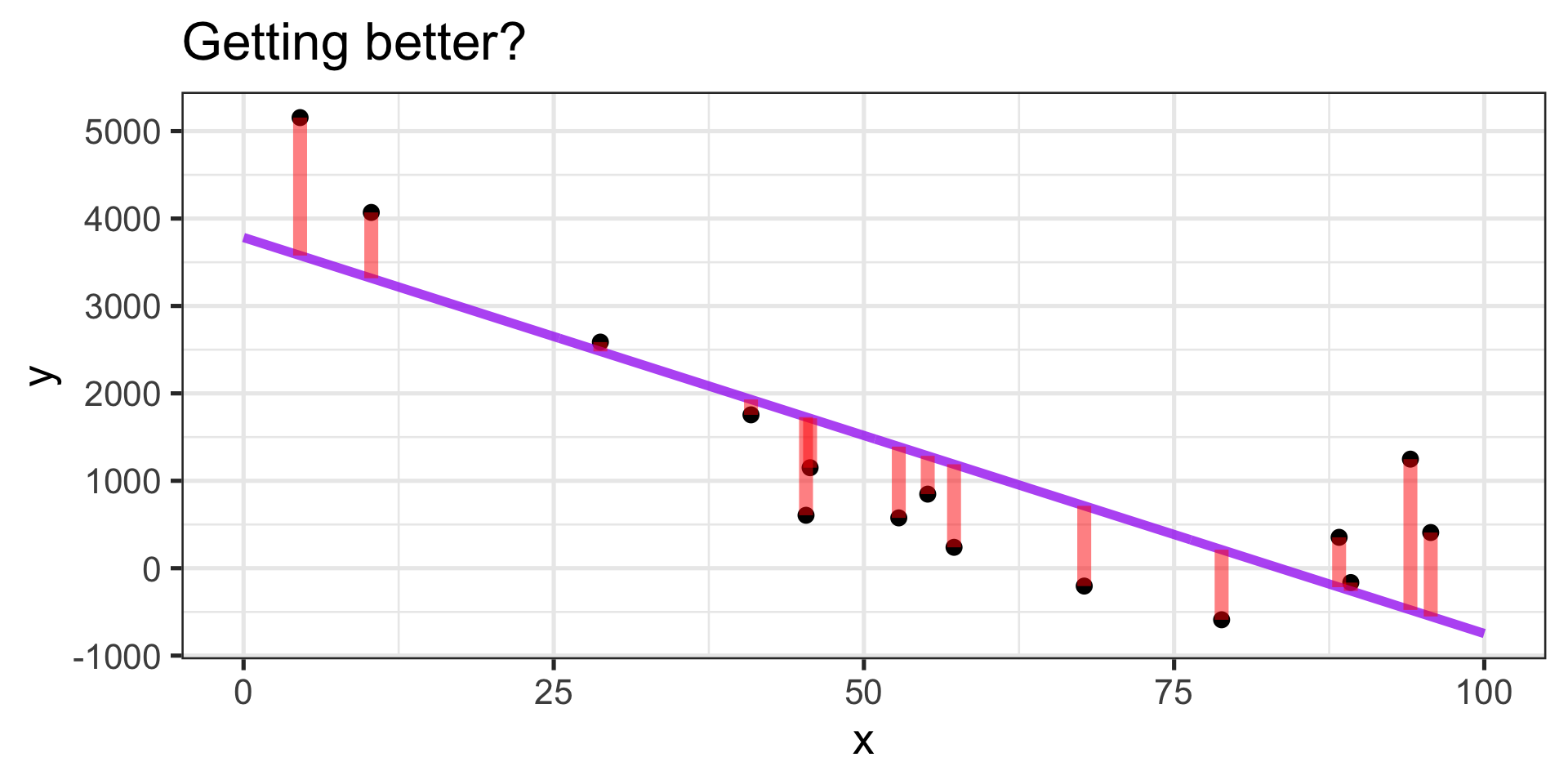
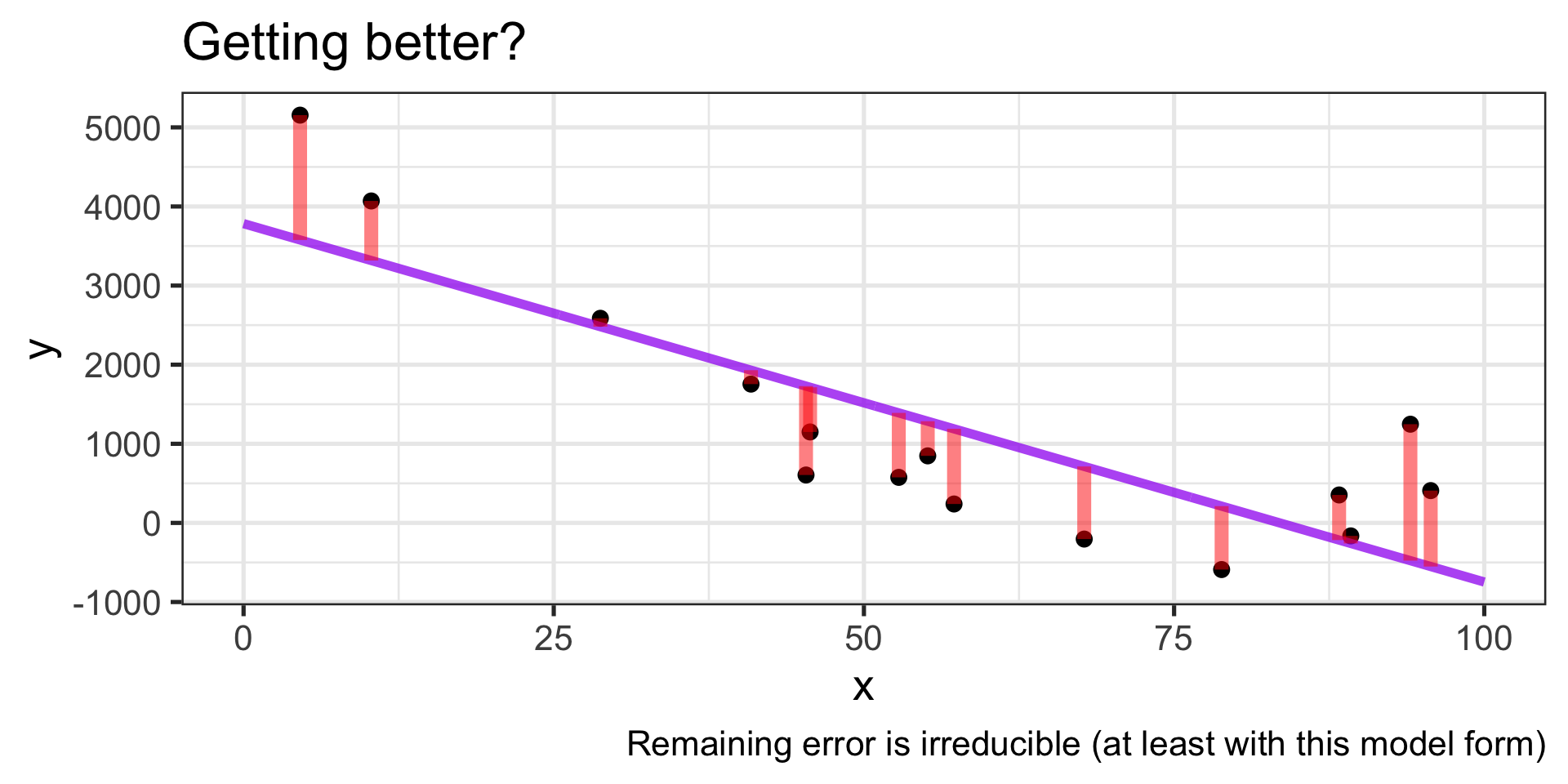
Statistical Learning in Pictures

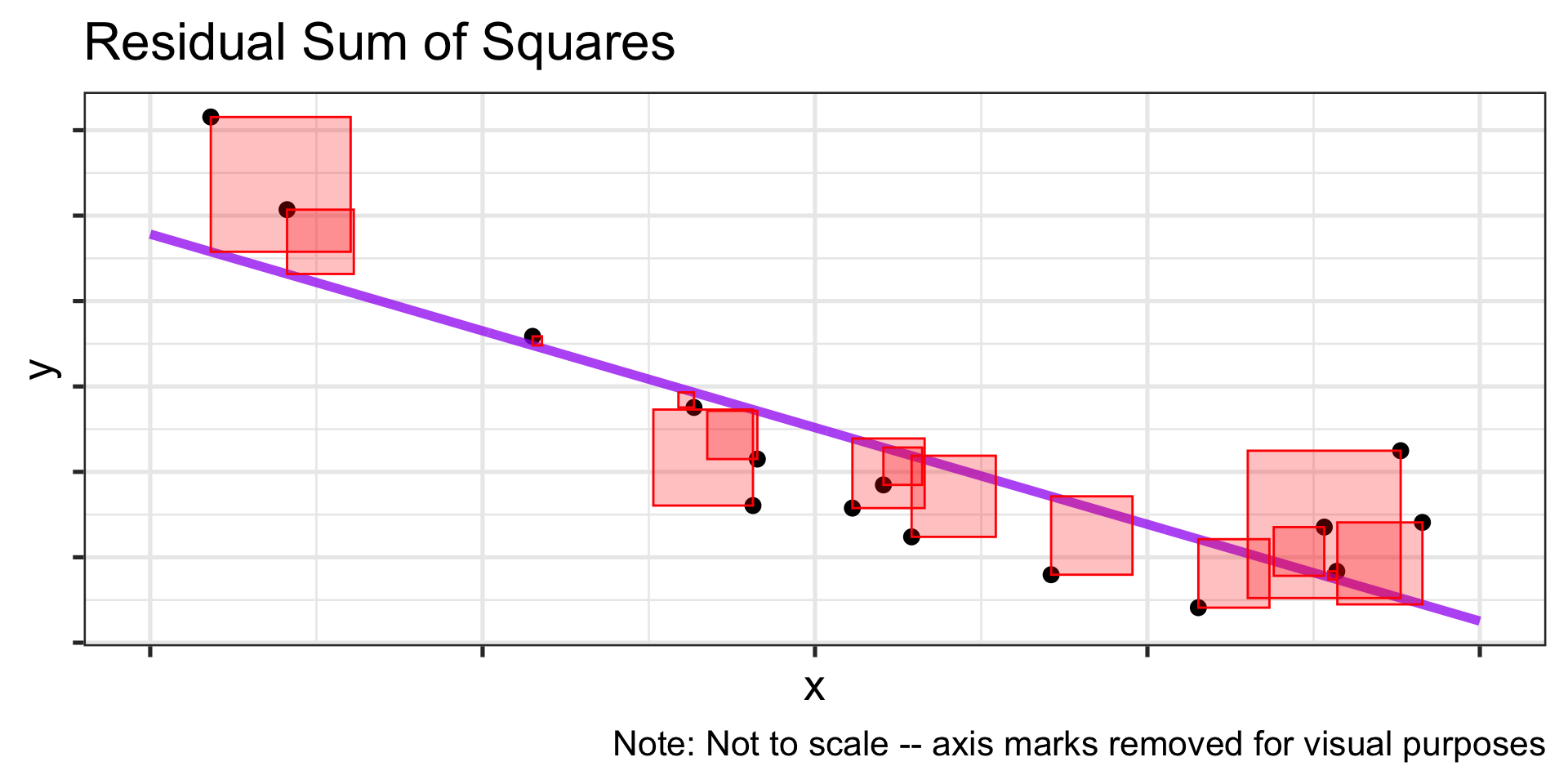
• Capturing the general trend?

  • …mostly

• Balanced errors?

  • ✓

How it works

In this case, we have \(\mathbb{E}\left[y\right] = \beta_0 + \beta_1\cdot x\) and we find \(\beta_0\) (intercept) and \(\beta_1\) (slope) to minimize the quantity

\[\sum_{i = 1}^{n}{\left(y_{\text{obs}_i} - y_{\text{pred}_i}\right)^2}\]

How it works

In this case, we have \(\mathbb{E}\left[y\right] = \beta_0 + \beta_1\cdot x\) and we find \(\beta_0\) (intercept) and \(\beta_1\) (slope) to minimize the quantity

\[\sum_{i = 1}^{n}{\left(y_{\text{obs}_i} - \left(\beta_0 + \beta_1\cdot x_{\text{obs}_i}\right)\right)^2}\]

• Changing \(\beta_0\) and/or \(\beta_1\) will change this sum.

How it works

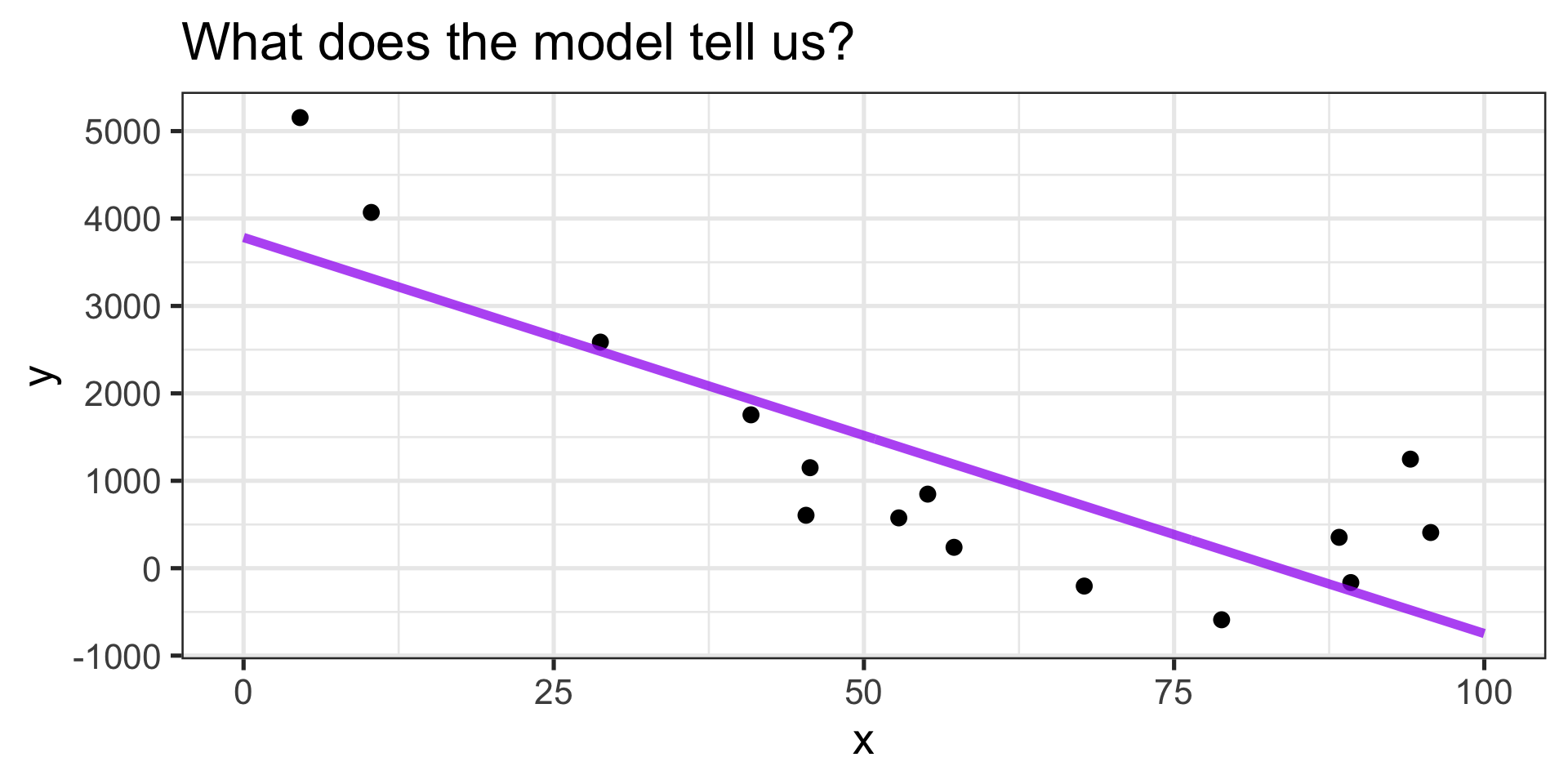
Interpreting the Model

\(\displaystyle{\mathbb{E}\left[y\right] = 3783.21 - 45.3\cdot x}\)

• The expected value of \(y\) when \(x = 0\) is \(3783.21\).
• As \(x\) increases, we expect \(y\) to decrease (on average).
• Given a unit increase in \(x\), we expect \(y\) to decrease by about \(45.3\) units.

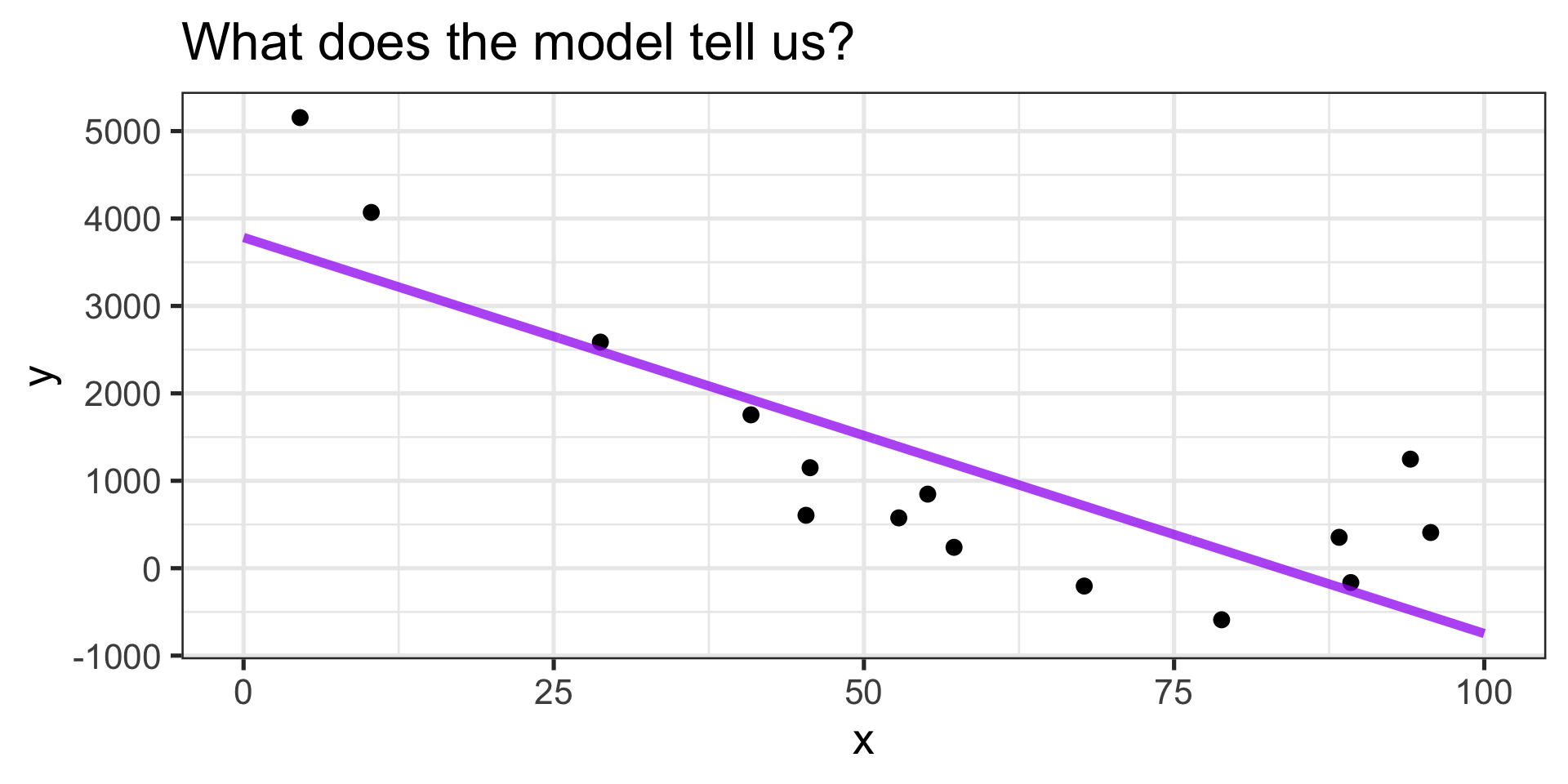
Interpreting the Model

\(\displaystyle{\mathbb{E}\left[y\right] = 3783.21 - 45.3\cdot x}\)

• The expected value of \(y\) when \(x = 0\) is \(3783.21\).
• As \(x\) increases, we expect \(y\) to decrease (on average).
• Given a unit increase in \(x\), we expect \(y\) to decrease by about \(45.3\) units.

Approach to Model Interpretation: In general, we’ll interpret the intercept (when appropriate) and the expected effect of a unit change in each predictor on the response

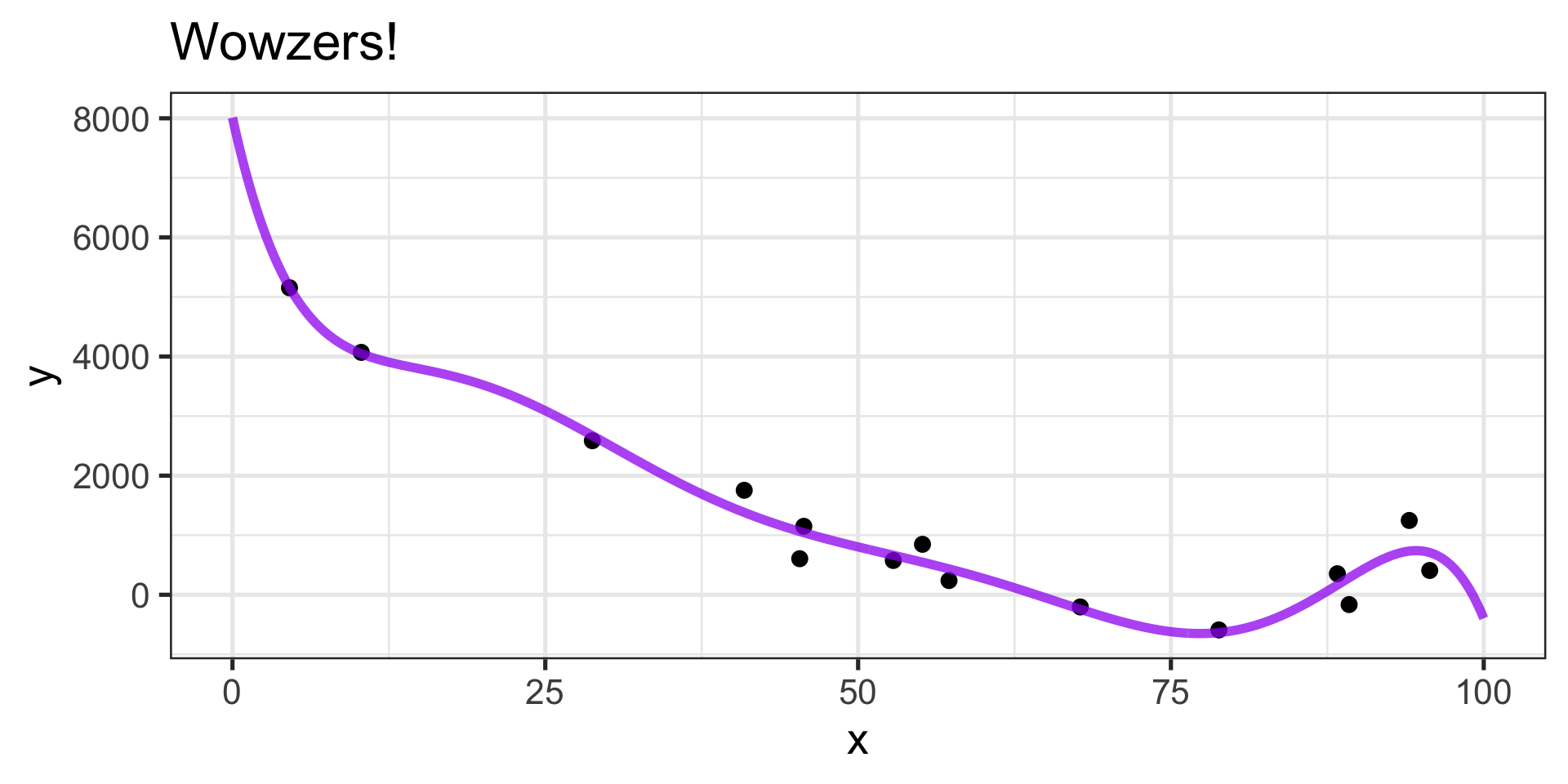
Can we find a better model?

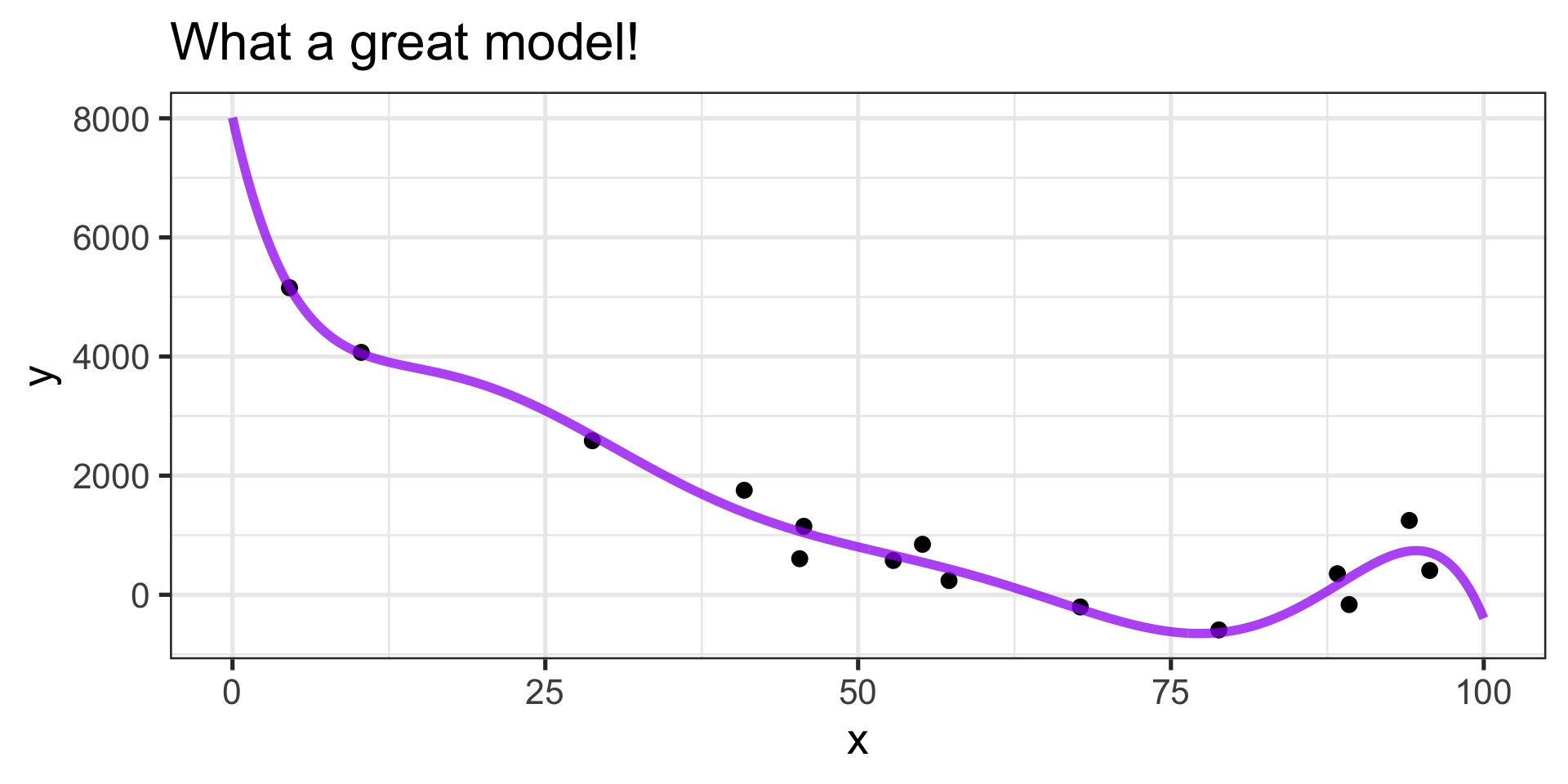
Can we interpret this model?

• The equation is \(\mathbb{E}\left[y\right] \approx 1202 - 4911x +3156x^2 + 784x^3 +\\ 409x^4 -215x^5 -7x^6 -516x^7\)
• No thanks…

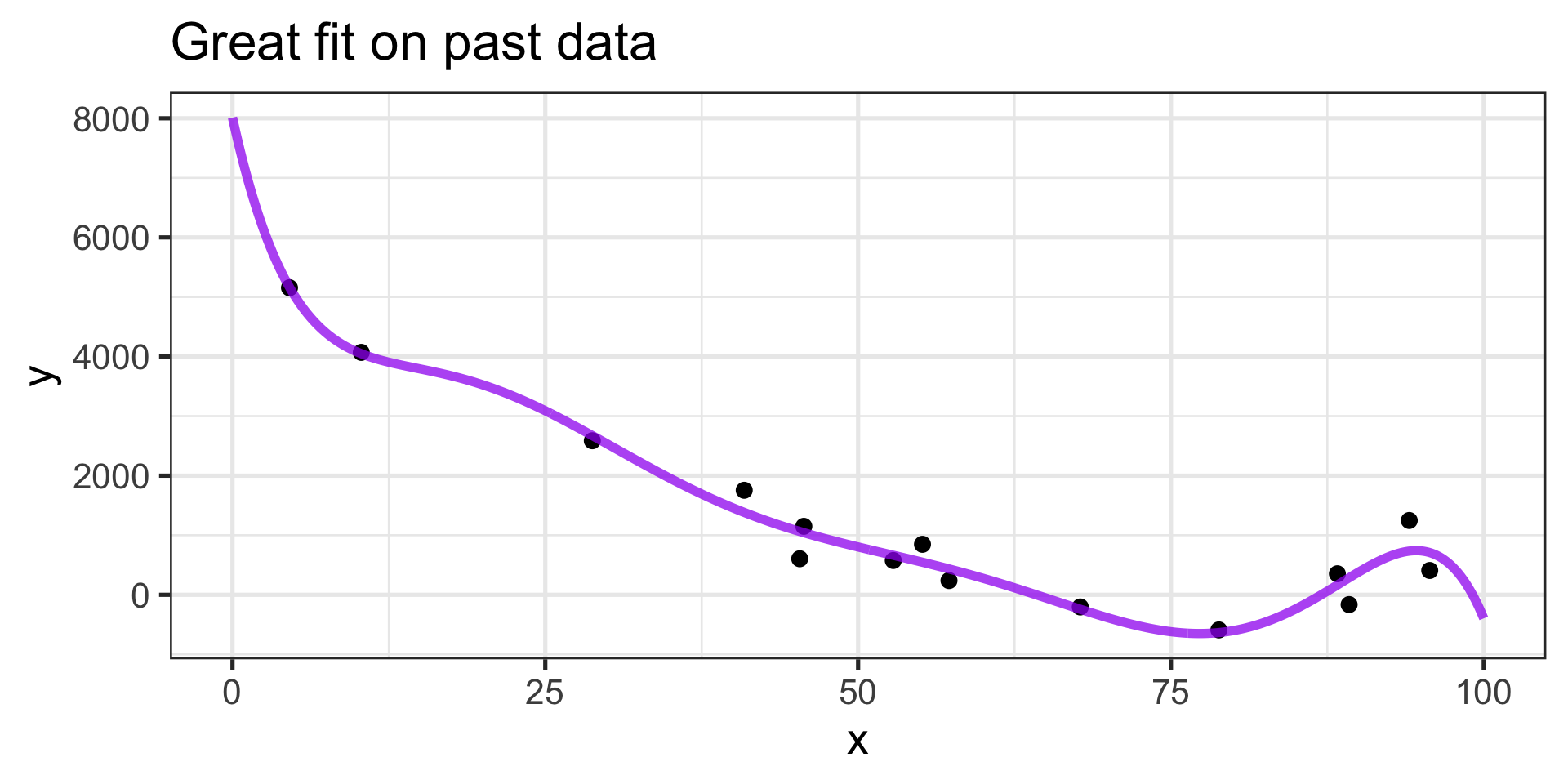
Do we expect this model to generalize well?

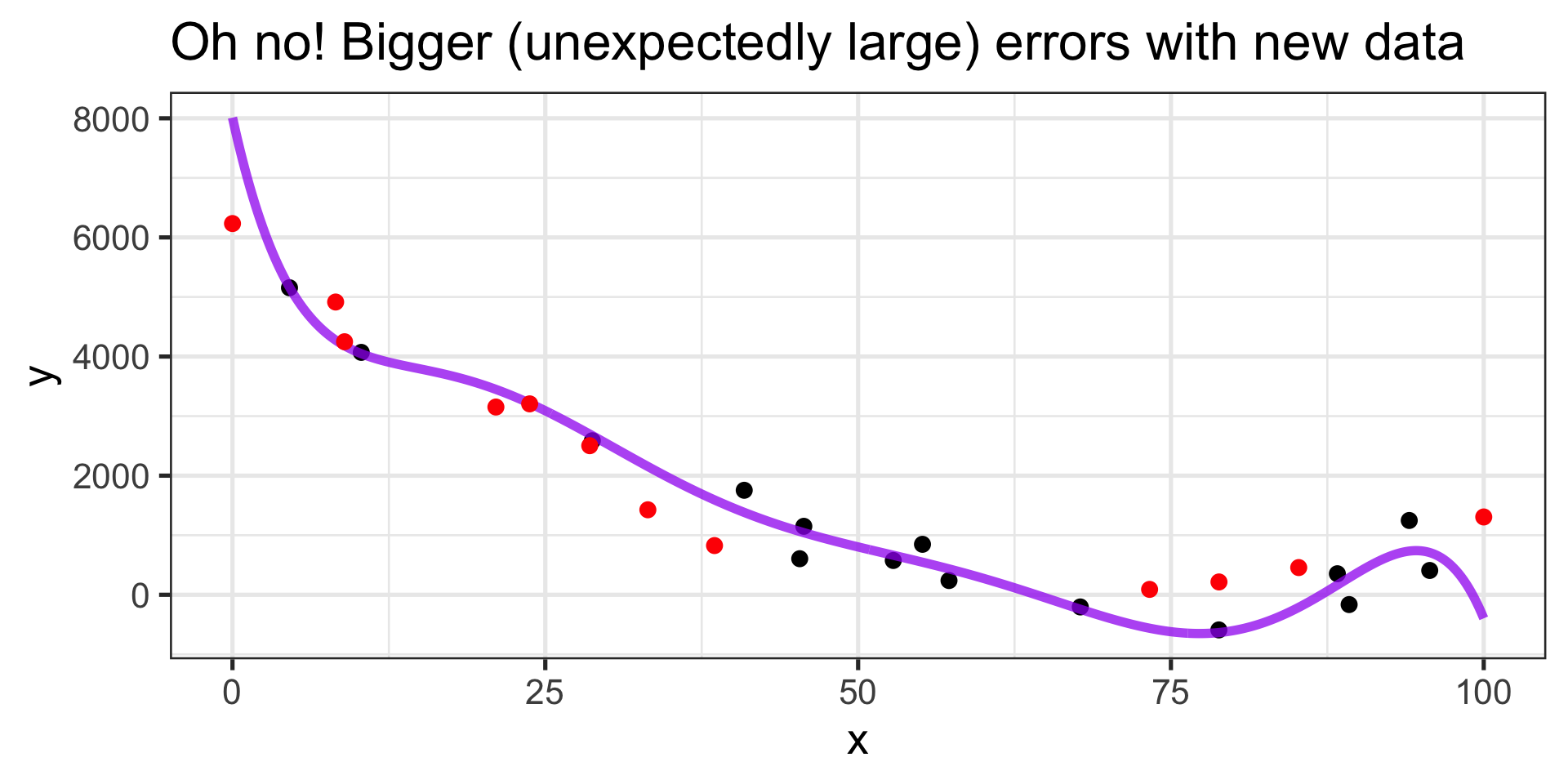
Do we expect this model to generalize well?

• Especially near \(x = 0\) and \(x = 100\)

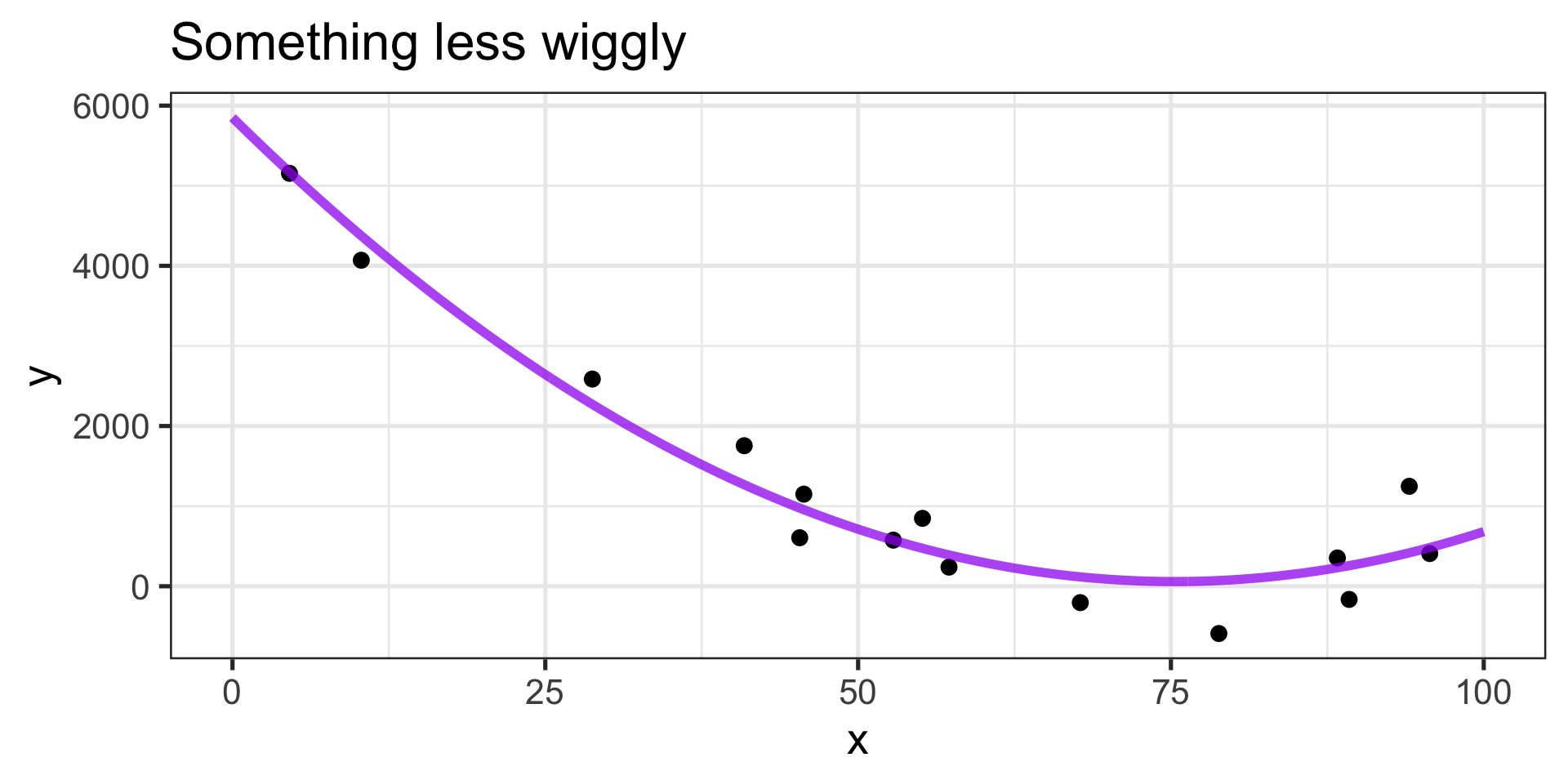
Is there a happy medium?

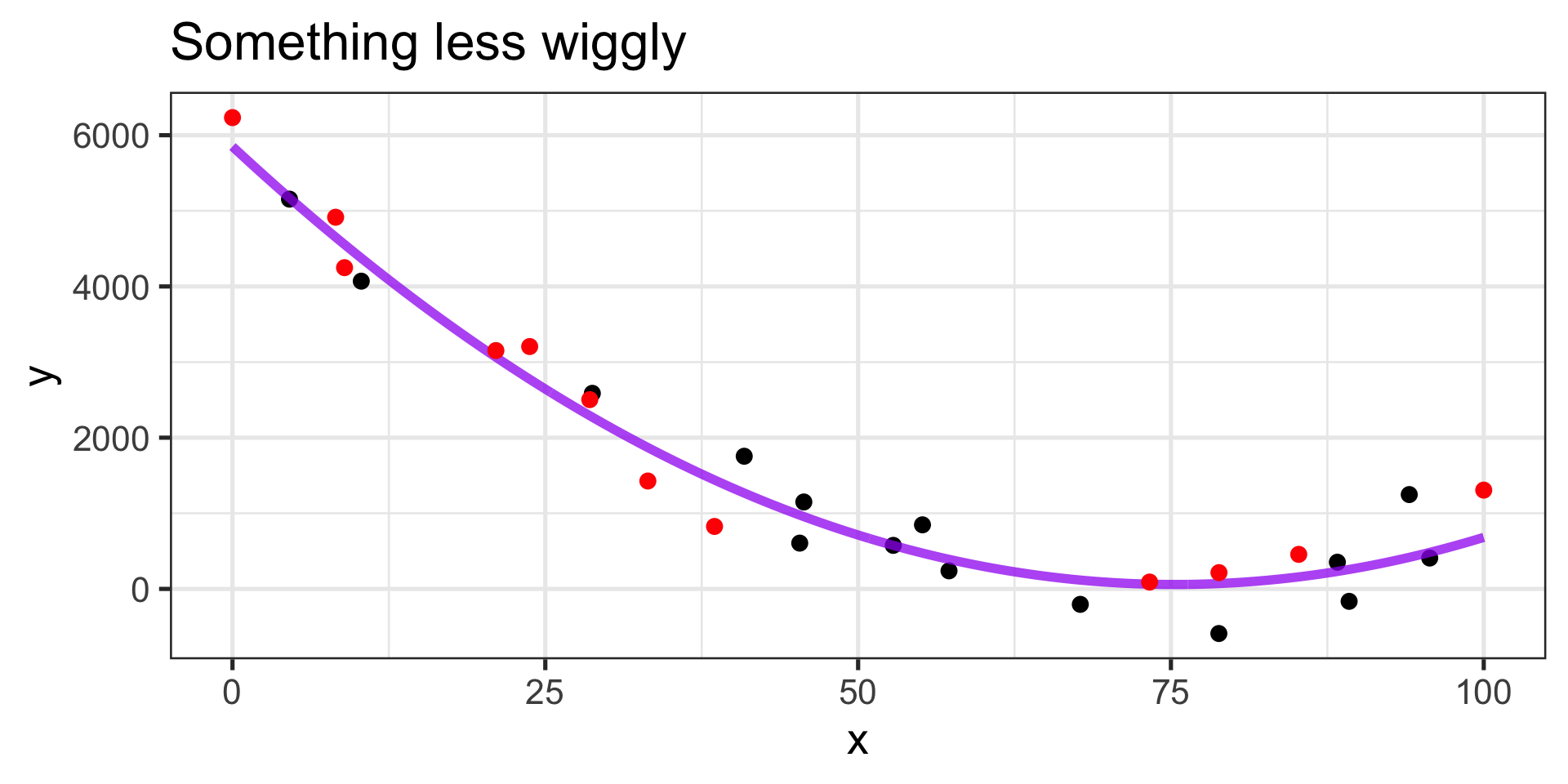
Is there a happy medium?

• Fits old and new observations similarly well

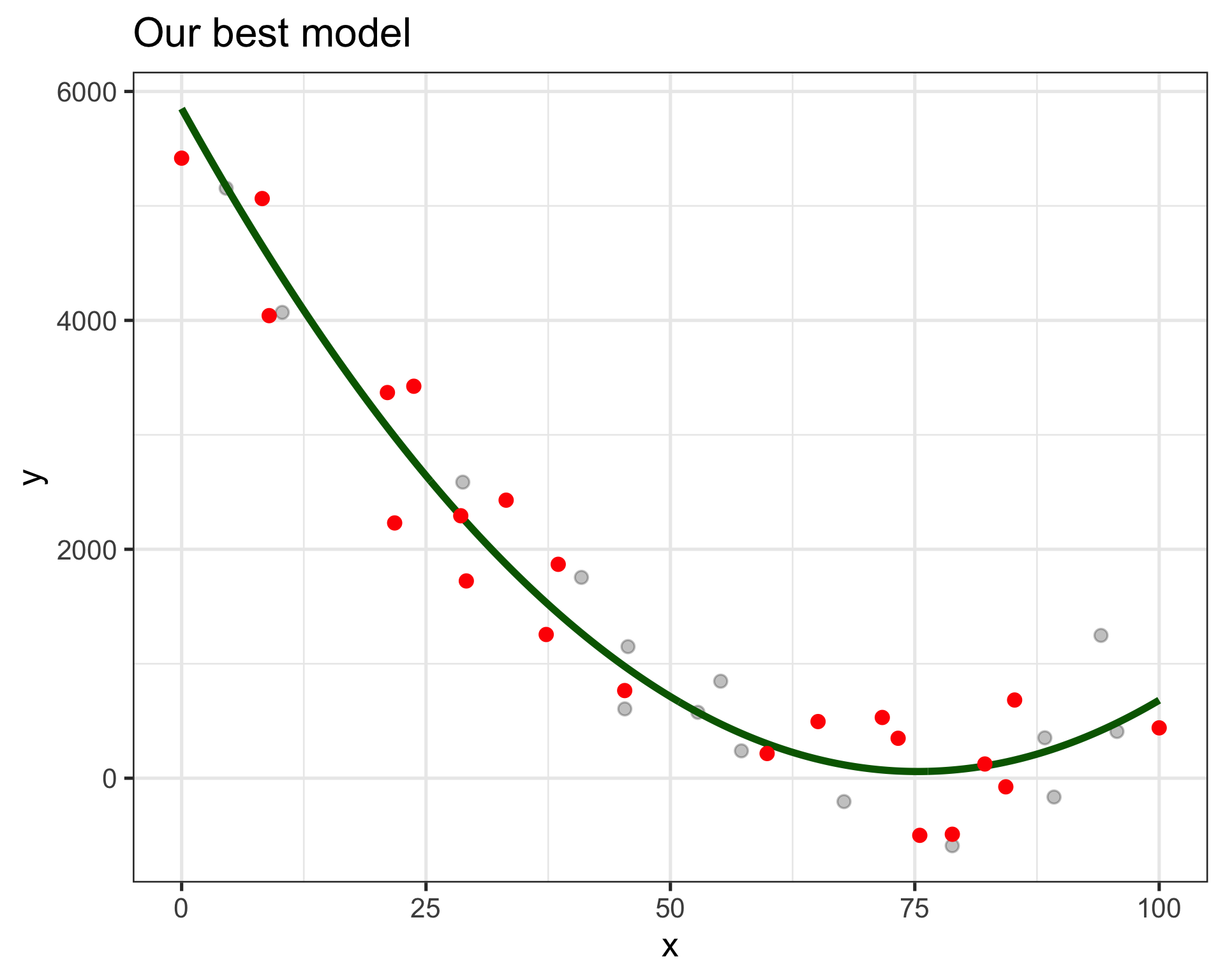
• Equation \(\displaystyle{\mathbb{E}\left[y\right] \approx 1202 -4912x + 3156x^2}\)

  • We’ll be able to interpret this

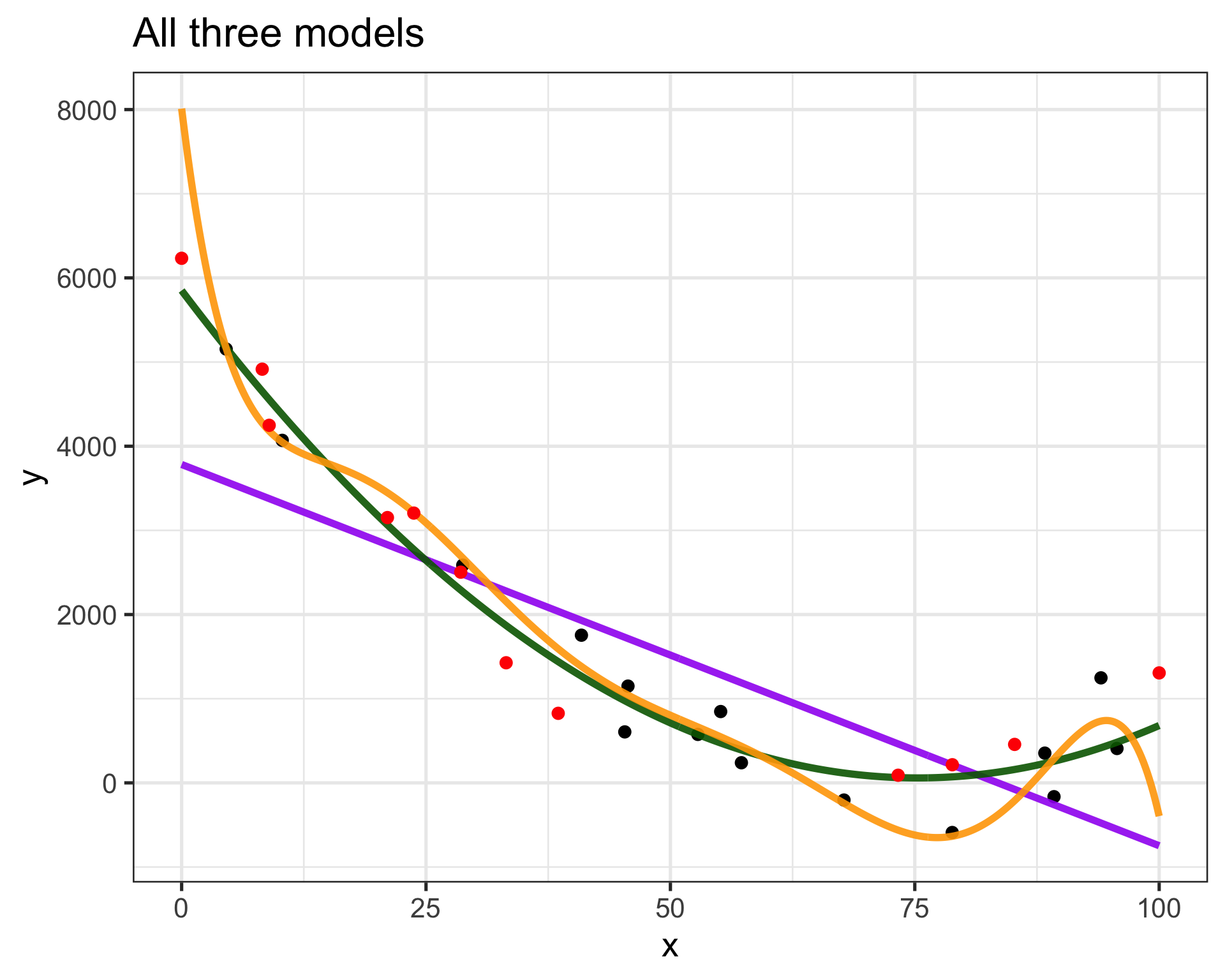
How do we know what model is right?

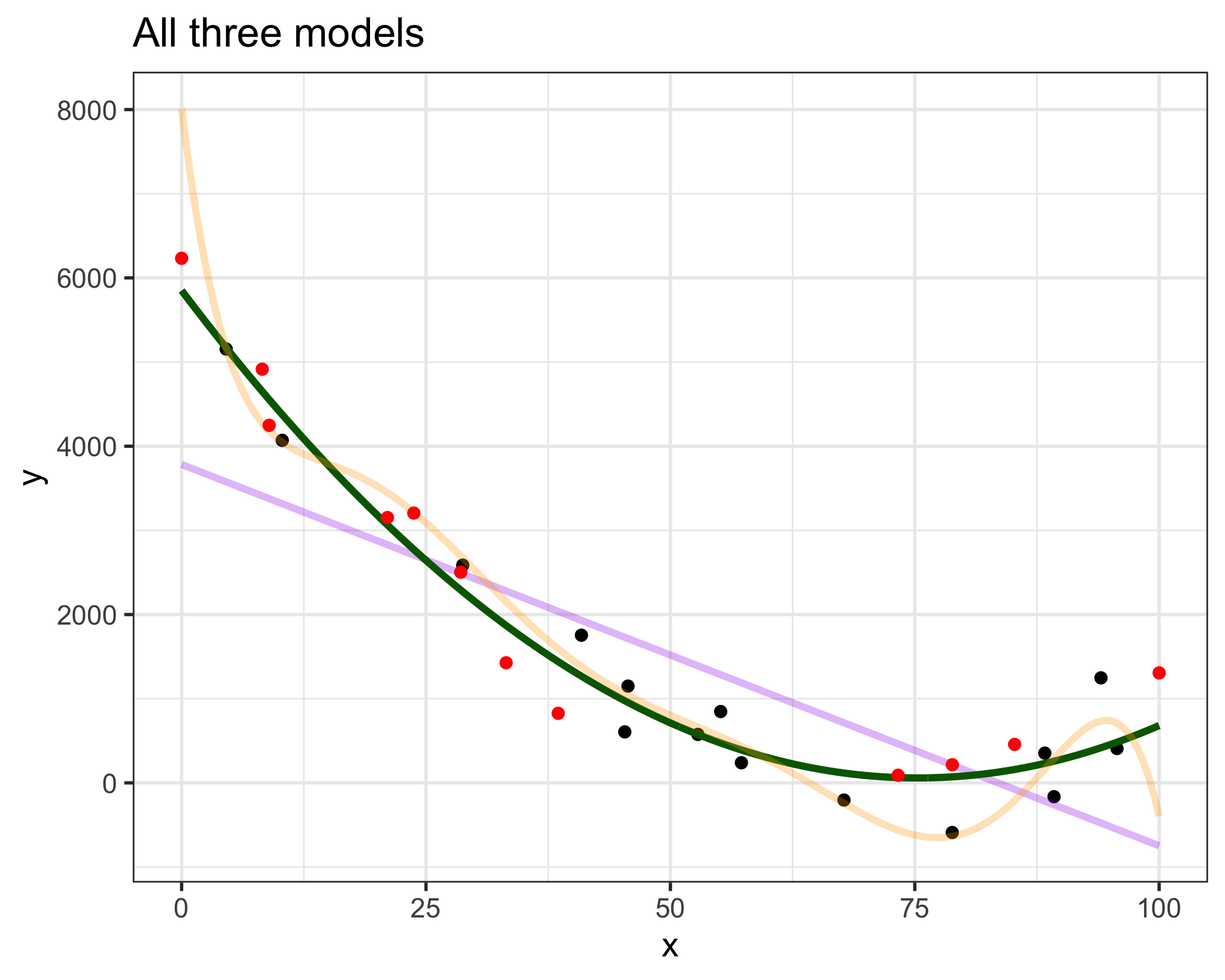
• The purple model is too straight
• The orange model is too wiggly
• The green model is just right

How do we know what model is right?

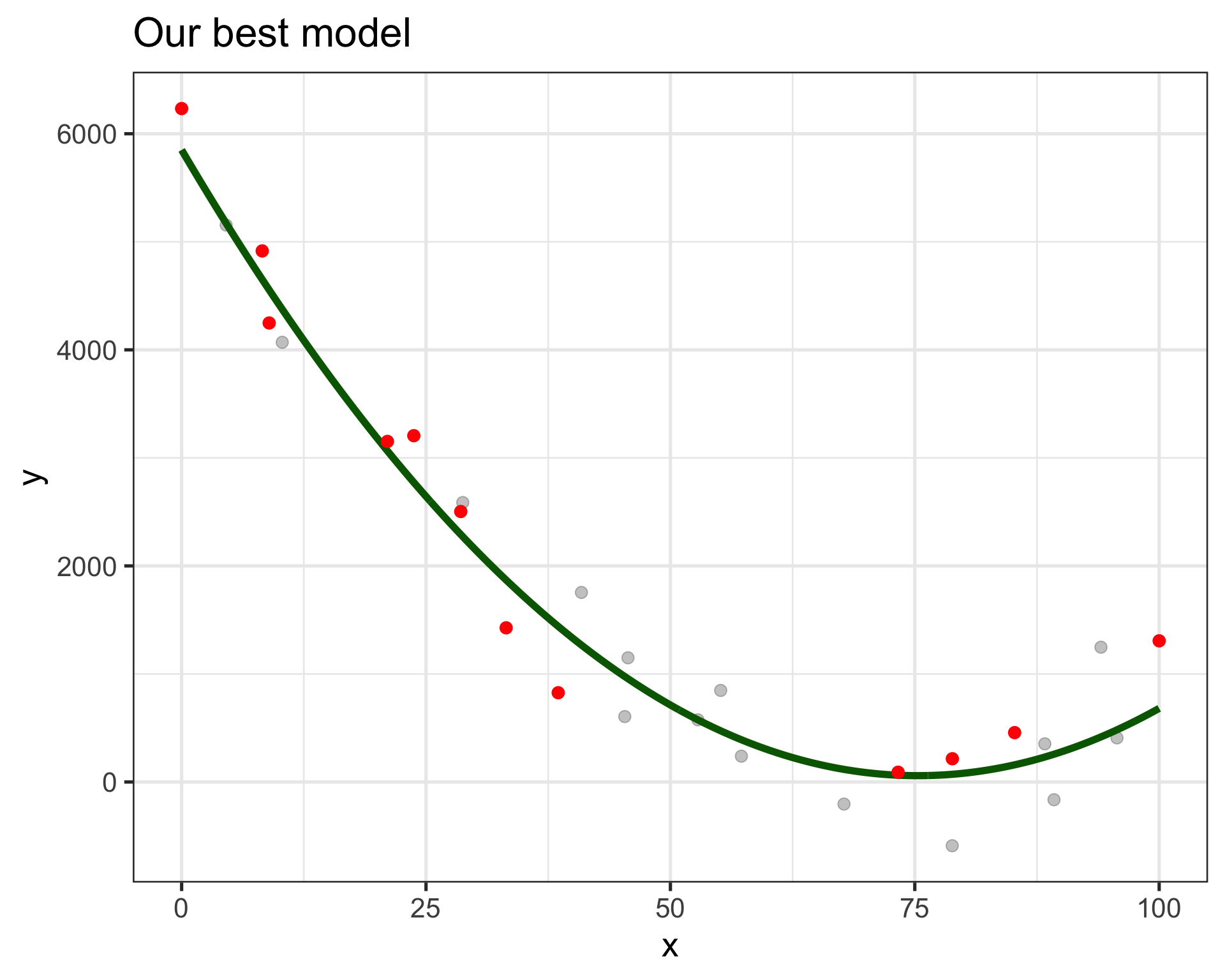
• We don’t want to wait for new data to know we are wrong.

  • Use some of our available data for training
  • And the rest for validation

Okay, but our predictions are all wrong…literally!

• All models are wrong, but some are useful, George Box (1976)
• Predictions will be wrong but, with some assumptions, they have value

Necessary Assumptions

For model and predictions

• Training data are random and representative of population.

  • Otherwise, we should not be modeling this way.

• Residuals (prediction errors) are normally distributed with mean \(\mu = 0\) and constant standard deviation \(\sigma\).

  • Allows construction of confidence intervals around predictions (making our models right).

Necessary Assumptions

For interpretations of coefficients (statistical learning / inference)

• No multicollinearity (predictors aren’t correlated with one another)

Summary

• Building models \(\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k\)

• Predicting a numerical response (\(y\)) given features (\(x_i\))

• Need data to build the models – some for training, some for validation

  • The \(\beta_i\)’s are parameters whose values are learned/estimated from training data

• Model predictions will be wrong

• As long as standard deviation of residuals (prediction errors) is constant, we can build meaningful confidence intervals for predictions

• Can interpret models to gain insight into relationships between predictor(s) and response

Competition Information

• Predict bicycle rental duration for a city bike share program

• Response: duration

• Predictors: You have access to nearly 40 explanatory variables which could be useful in predicting the duration of a rental.

  • Date and time information
  • Origin of the rental
  • Station and city information
  • Weather-based features
  • Bicycle availability

How this works

• Six assignments to guide you.
• You’ll take data provided by the city bike share program and build models.
• Kaggle will assess the predictions generated by your models.
• A live leaderboard will let you know approximately where you stand, using a portion of the competition data.
• You’ll talk with one other about modeling ideas and perfomance differences.
• People might choose share their strategies, while others might not – this is a competition after all.

Clarification: All work submitted on these competitions must reflect your own analytical thinking and modeling decisions.

• It is acceptable to ask peers for advice and to share what they did, but direct model-based code-sharing is not permitted.
• Use of AI tools is limited to debugging or correcting errors in code that you have written.
• Using AI to generate models, analysis, or interpretations is inconsistent with the goals of these assignments, and is prohibited.

Connection to Debrief Meetings: Your submitted competition work will serve as part of the foundation for our debrief meetings. In these meetings, you will be expected to explain and justify your modeling choices, performance results, and interpretations. The purpose of these discussions is to ensure that the submitted work accurately reflects your understanding.

Why?

• Interest in homework assignments generally ends after they’re turned in and graded.
• The competition assignments and competitive environment ask you to iterate on previous work.
• You’ll almost surely be interested in what other people have done, especially if their models have performed better than yours.
• You’ll talk with one another about strategies and modeling choices.
• You’ll be motivated to improve your model even between assignments.

What past students say

• The competition is fun
• It is motivating
• I learned more because I wanted to place better in the competition
• Talking with others about their models made me more confident in my understanding of course material

What you are building

• An analytics report
• You’ll be building models and (more importantly) writing about your modeling choices and the performance of your models
• Six assignments – each focusing on part(s) of the modeling process and analytics report
• Prepares you for the final project, where you’ll do all this over again on a data set you identified and care about

Next Time…

• Way fewer slides! 🤕
• An introduction to R
• Getting our hands dirty!

Homework: Start Competition Assignment 1 – join the competition, read the details, download the data, and start writing a Statement of Purpose