Interpretation of Marginal Effects with {marginaleffects}
October 25, 2024
Motivation
Recently, we’ve introduced utilization of higher-order terms to add flexibility to our models
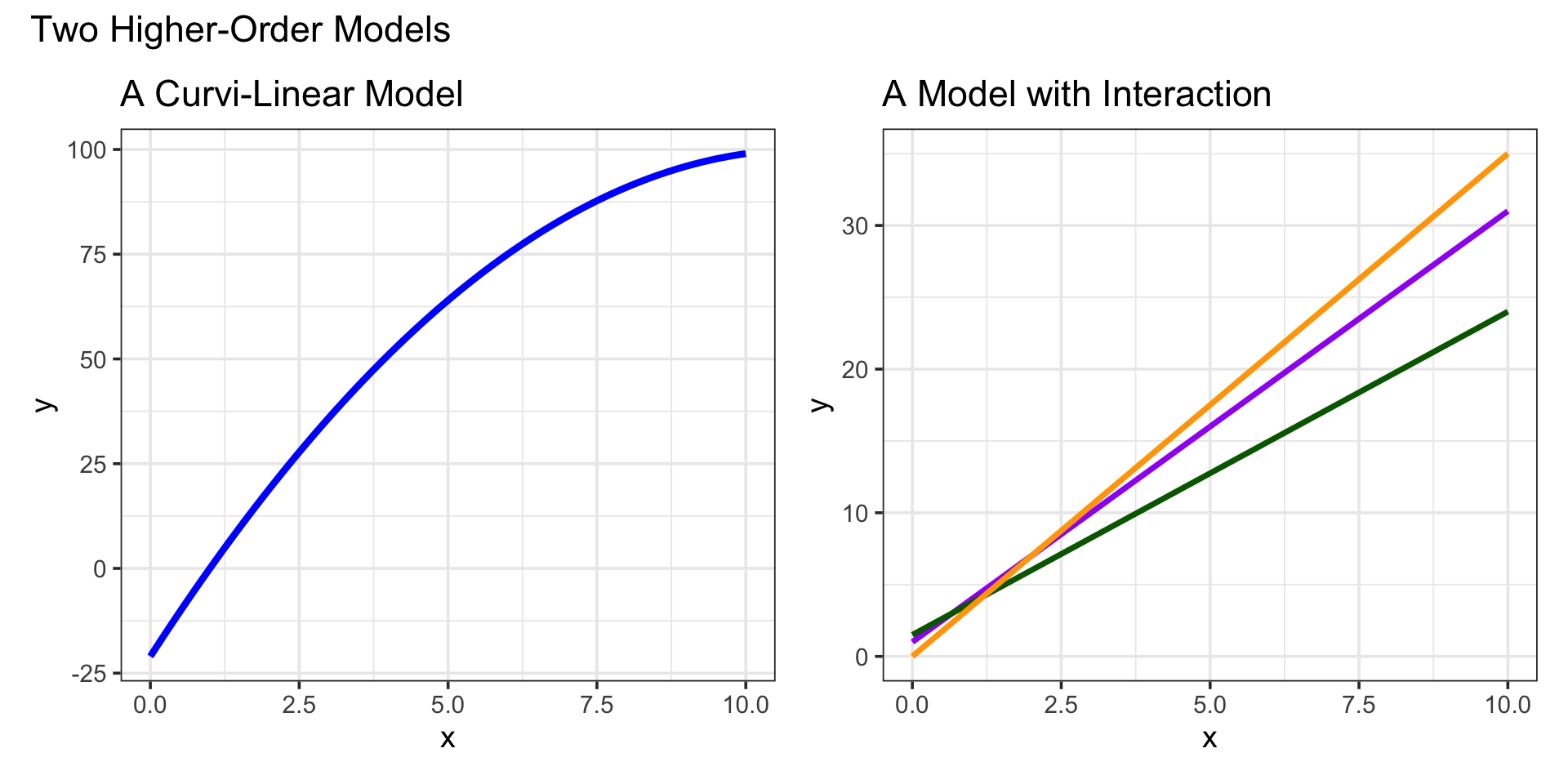
The use of these higher-order terms allows us to model more complex relationships between predictor(s) and our response, but this comes at costs…
Models including higher-order terms are more difficult to interpret
Note: There are other costs/risks too, but we’ll save those for another day
Motivation
Interpreting the expected effect of a unit increase in a predictor on our response requires calculus
Interpreting a “Quadratic Predictor”: Recall that if a model contains a predictor \(x\) such that \(\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x + \beta_2 x^2 + \cdots\), where \(x\) appears in no terms other than those listed, then
The expected effect of a unit increase in \(x\) on the response \(y\) is an increase of about \(\beta_1 + 2x\beta_2\)
Interpreting a Predictor Involved in Interaction: If a model contains a predictor \(x\) which is involved in an interaction with another predictor \(w\), such that \(\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x + \beta_2 xw + \cdots\) and \(x\) appears in no other terms, then
The expected effect of a unit increase in \(x\) on the response \(y\) is an increase of about \(\beta_1 + \beta_2 w\)
Both of these expressions are obtained by taking the partial derivative of our model with respect to the predictor \(x\)
Motivation
Calculus isn’t a requirement for this course, but those of you who don’t have a background in it are somewhat disadvantaged with the tools for interpretation that I’ve given you so far
You could memorize the \(\beta_1 + 2x\beta_2\) and \(\beta_1 + w\beta_2\) expressions for the interpretation of a predictor used in a quadratic term and a predictor involved in an interaction, respectively
But if we move to more complex models, then you’d need to memorize more complex expressions
For Example: Given the model \[\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_1 x_2 + \beta_4x_1^2 + \beta_5x_1^2x_2\]
the expected effect of a unit increase in \(x_1\) on the response \(y\) is an increase of about \(\beta_1 + x_2\beta_3 + 2x_1\beta_4 + 2x_1 x_2\beta_5\)
Memorizing expressions is an inefficient use of our time and brain capacity
Motivation
Knowing some calculus makes our interpretation work easier and makes you more versatile, but…
You don’t need to learn calculus right now – consider learning it in the future though!
Luckily, the {marginaleffects} package can help us in the immediate term
Note: Even with {marginaleffects}, I suggest eventually learning some basic calculus if you are interested in statistical modeling. Having that background can help you identify suspicious results rather than blindly reporting the results of a function call.
Additional Resource: Andrew Heiss has a truly excellent and detailed blog post on marginal effects and calculus, including how to use
{marginaleffects}(and similar packages), comparisons of different types of marginal effects, and how to interpret results
Highlights
- We have just one goal here – learn how to use
{marginaleffects}to help us analyze the effect of a unit increase in a predictor on a response - We’ll start with a simple linear regression model so that we know everything is working correctly
- Next, we’ll move to a curvilinear model with a second-degree term on the sole predictor, \(x\)
- We’ll then fit a super-flexible fifth-degree model with a sole predictor, \(x\), and see how
{marginaleffects}reports the marginal effect of \(x\) on \(y\) - Finally, we’ll move to a pair of interaction models – one with a linear association and the other with a curved association
Marginal Effects for Simple Linear Regression
\[\mathbb{E}\left[y\right] = \beta_0 + \beta_1 \cdot x\]
We know what to expect here – the effect of a unit increase in \(x\) should be an expected increase in \(y\) by about \(\beta_1\)
That is, the marginal effect of \(x\) on \(y\) is constant, for this model
Let’s fit our simple linear regression model to this data and then examine the marginal effects
Marginal Effects for Simple Linear Regression
Code
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.0789667 | 0.9303051 | 0.0848826 | 0.9325279 |
| x | 3.0606531 | 0.1593729 | 19.2043484 | 0.0000000 |
Marginal Effects for Simple Linear Regression
Code
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.0789667 | 0.9303051 | 0.0848826 | 0.9325279 |
| x | 3.0606531 | 0.1593729 | 19.2043484 | 0.0000000 |
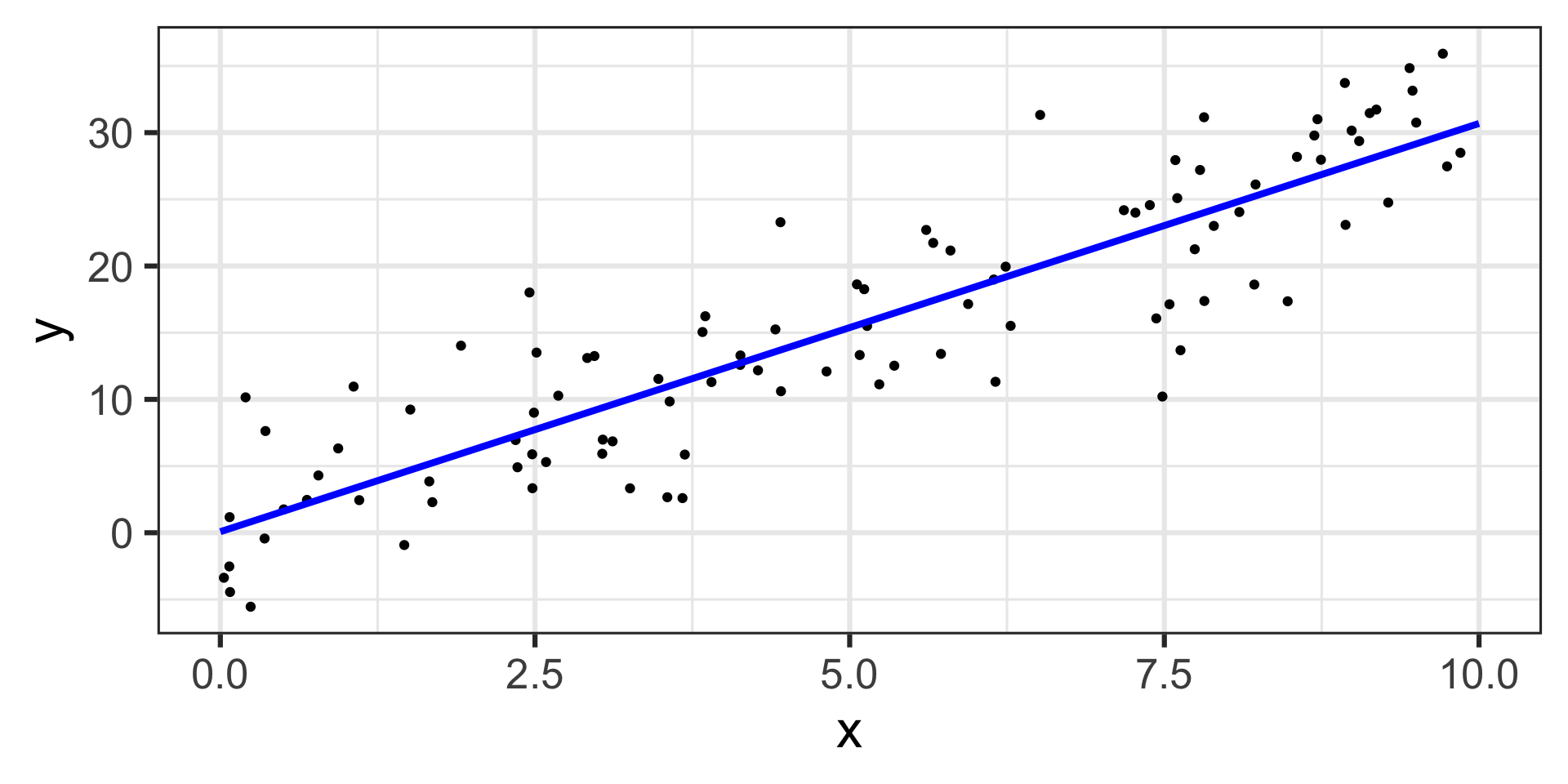
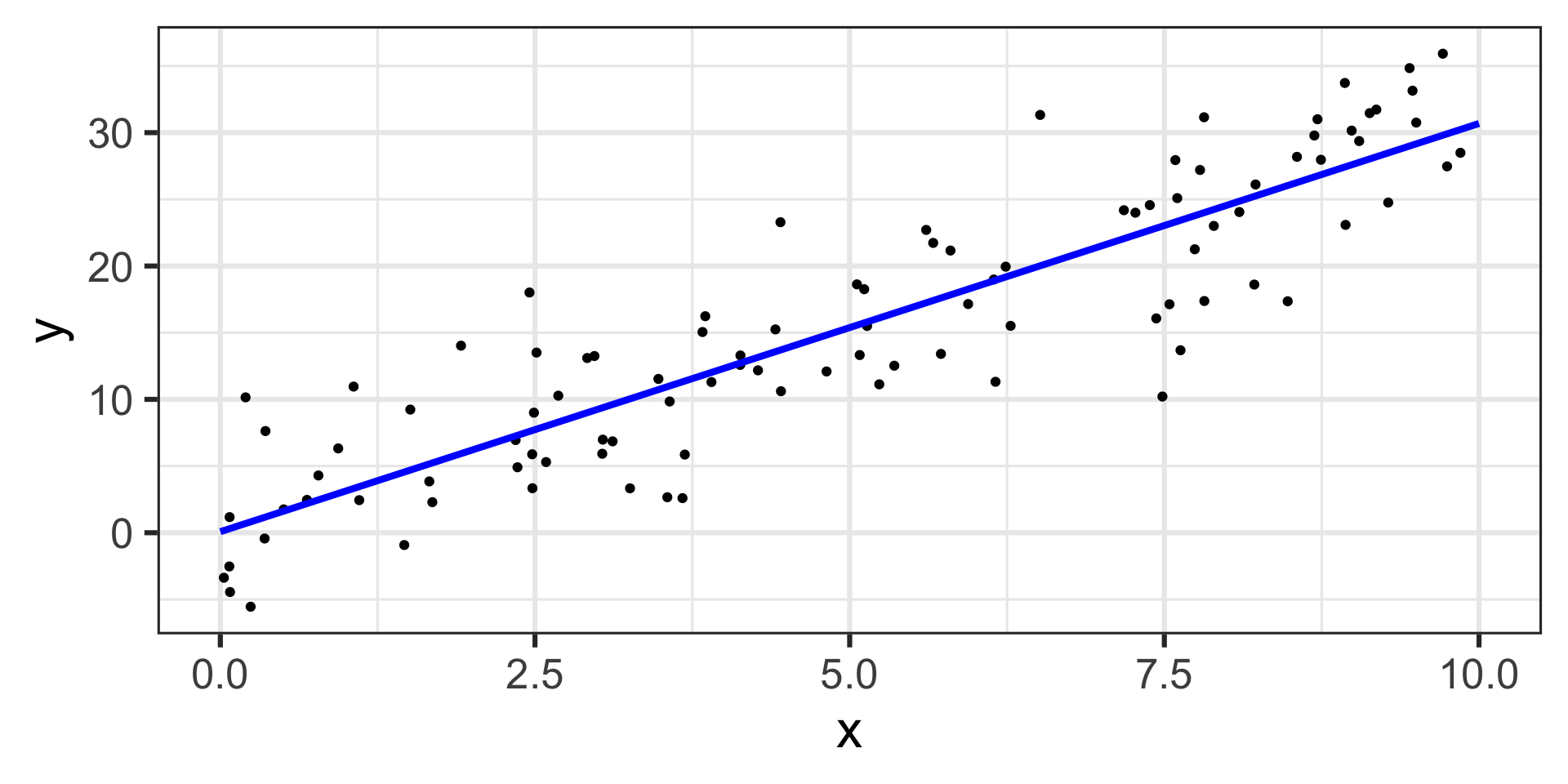
\[\mathbb{E}\left[y\right] = 0.079 + 3.06\cdot x\]
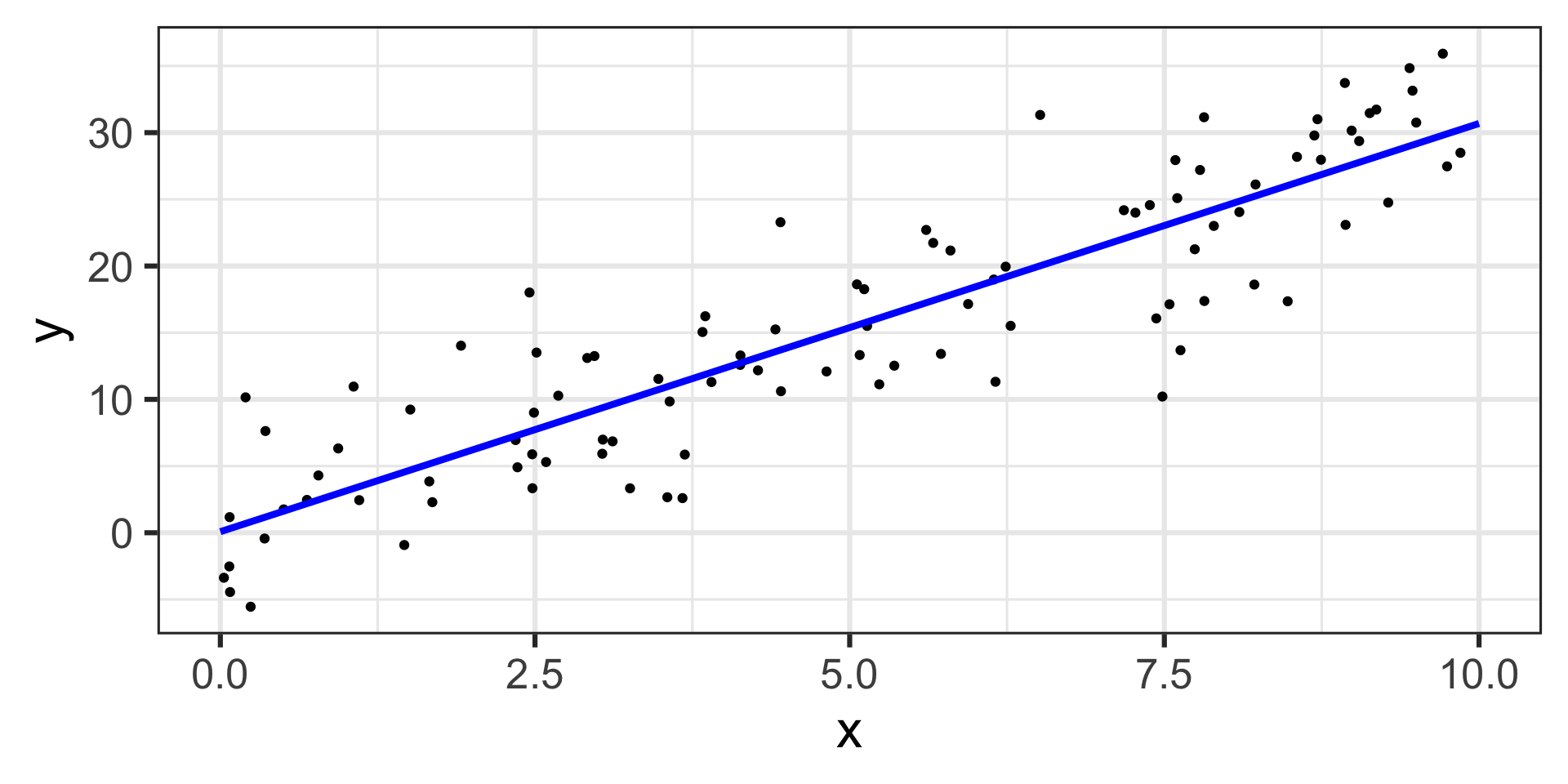
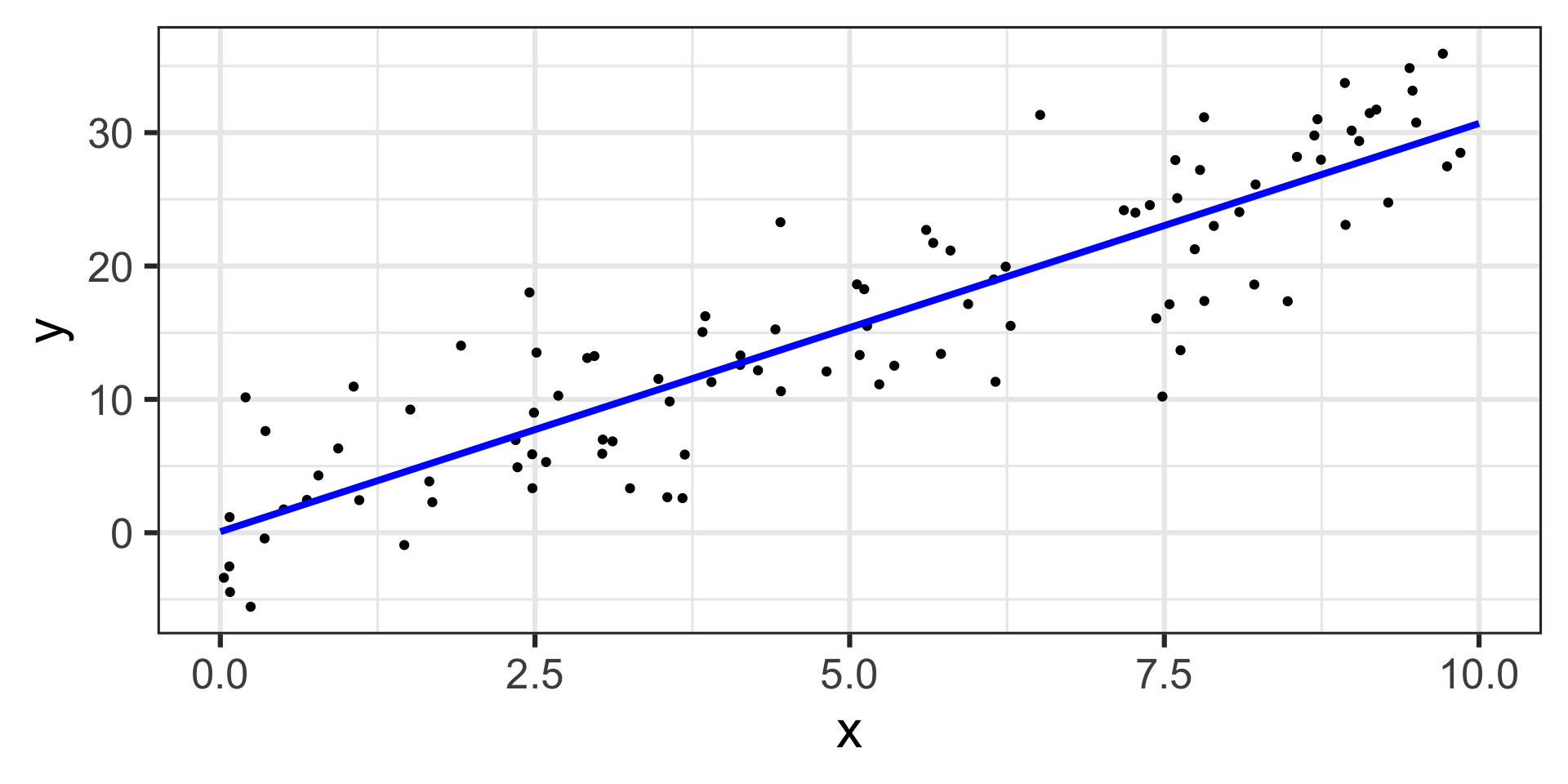
The estimated model appears below, on top of the training data.
Marginal Effects for Simple Linear Regression
Code
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.0789667 | 0.9303051 | 0.0848826 | 0.9325279 |
| x | 3.0606531 | 0.1593729 | 19.2043484 | 0.0000000 |
\[\mathbb{E}\left[y\right] = 0.079 + 3.06\cdot x\]
The estimated model appears below, on top of the training data.
Marginal Effects for Simple Linear Regression
Code
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.0789667 | 0.9303051 | 0.0848826 | 0.9325279 |
| x | 3.0606531 | 0.1593729 | 19.2043484 | 0.0000000 |
\[\mathbb{E}\left[y\right] = 0.079 + 3.06\cdot x\]
The estimated model appears below, on top of the training data.
Now that we have our model, let’s use {marginaleffects} to determine the marginal effect of \(x\) on \(y\)
Marginal Effects for Simple Linear Regression
Code
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.0789667 | 0.9303051 | 0.0848826 | 0.9325279 |
| x | 3.0606531 | 0.1593729 | 19.2043484 | 0.0000000 |
\[\mathbb{E}\left[y\right] = 0.079 + 3.06\cdot x\]
The estimated model appears below, on top of the training data.
Now that we have our model, let’s use {marginaleffects} to determine the marginal effect of \(x\) on \(y\)
Code
mfx <- lr_fit %>%
extract_fit_engine() %>%
slopes(my_data) %>%
tibble()
mfx %>%
ggplot() +
geom_ribbon(aes(x = x,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x,
y = estimate),
color = "black",
linetype = "dashed") +
coord_cartesian(
ylim = c(-0.5, 5)
) +
labs(x = "x",
y = "Marginal Effect of x on y") +
theme_bw(base_size = 24)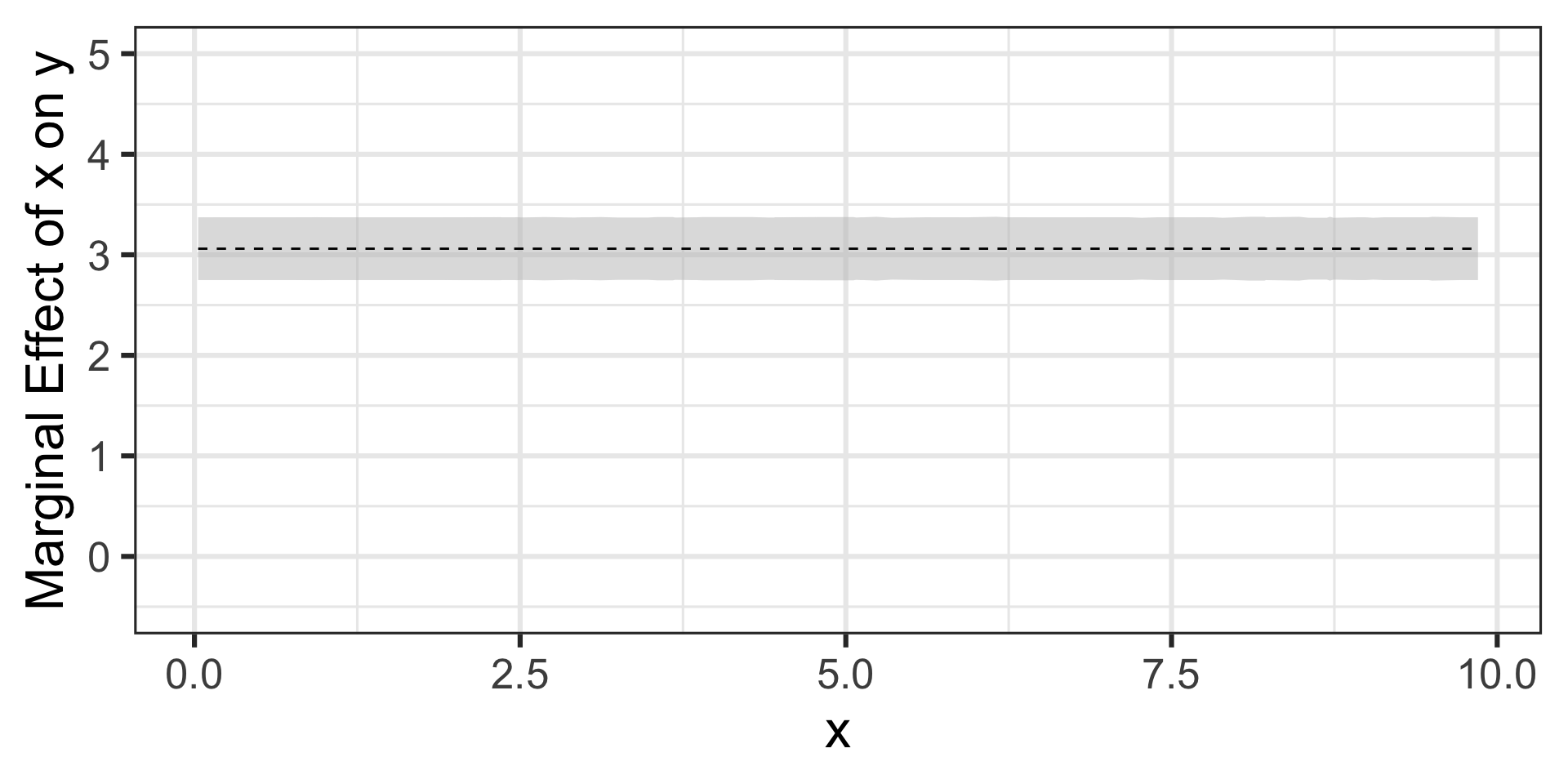
Marginal Effects for Simple Linear Regression
Code
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.0789667 | 0.9303051 | 0.0848826 | 0.9325279 |
| x | 3.0606531 | 0.1593729 | 19.2043484 | 0.0000000 |
\[\mathbb{E}\left[y\right] = 0.079 + 3.06\cdot x\]
The estimated model appears below, on top of the training data.
As expected, a constant marginal effect at a height of \(\beta_1\)
Now that we have our model, let’s use {marginaleffects} to determine the marginal effect of \(x\) on \(y\)
Code
mfx <- lr_fit %>%
extract_fit_engine() %>%
slopes(my_data) %>%
tibble()
mfx %>%
ggplot() +
geom_ribbon(aes(x = x,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x,
y = estimate),
color = "black",
linetype = "dashed") +
coord_cartesian(
ylim = c(-0.5, 5)
) +
labs(x = "x",
y = "Marginal Effect of x on y") +
theme_bw(base_size = 24)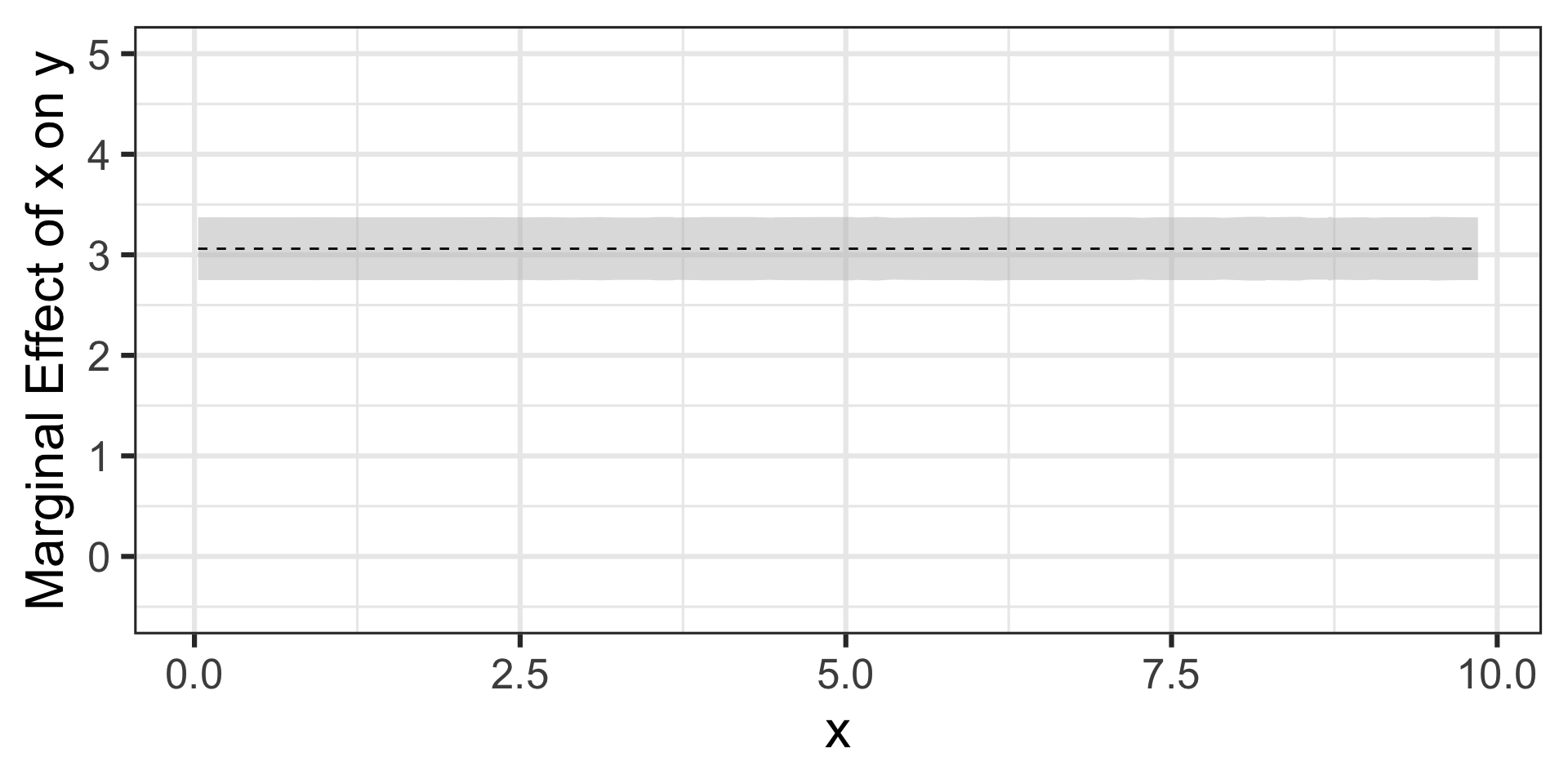
Marginal Effects for a Model with a Quadratic Term
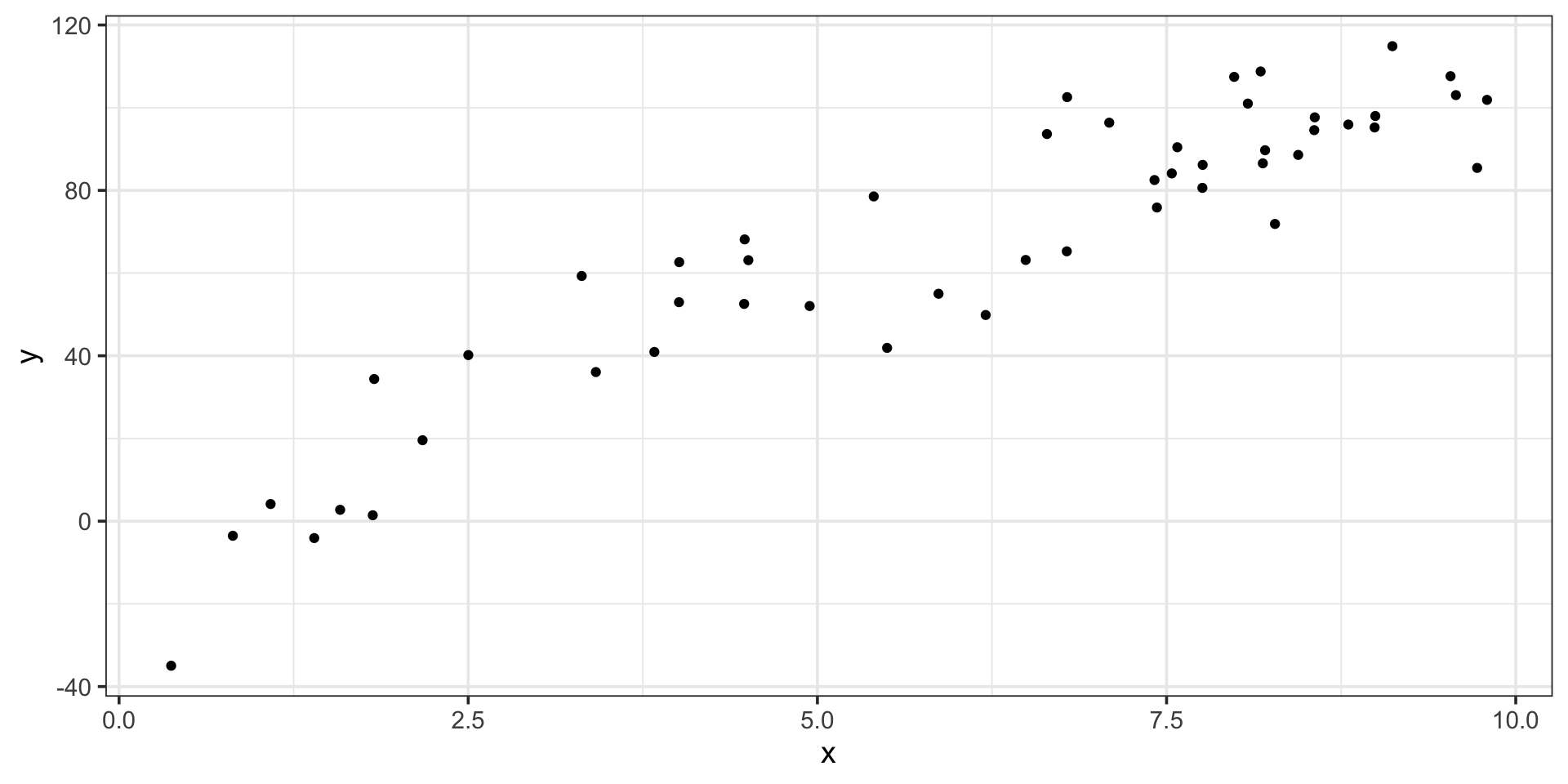
\[\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x + \beta_2 x^2\]
Again, we know what to expect – the effect of a unit increase in \(x\) should be an expected increase in \(y\) by about \(\beta_1 + 2x\beta_2\)
That is, the marginal effect of \(x\) on \(y\) will change based on the value of \(x\) for this model
As we did with the last scenario, we’ll fit our model and examine the marginal effects
Marginal Effects for a Model with a Quadratic Term
Code
clr_spec <- linear_reg() %>%
set_engine("lm")
clr_rec <- recipe(y ~ x, data = my_data) %>%
step_poly(x, degree = 2, options = list(raw = TRUE))
clr_wf <- workflow() %>%
add_model(clr_spec) %>%
add_recipe(clr_rec)
clr_fit <- clr_wf %>%
fit(my_data)
clr_fit %>%
extract_fit_engine() %>%
tidy() %>%
kable() %>%
kable_styling(font_size = 16)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -23.7867692 | 7.0140682 | -3.391294 | 0.0014188 |
| x_poly_1 | 21.8554094 | 2.9863758 | 7.318372 | 0.0000000 |
| x_poly_2 | -0.9402959 | 0.2744471 | -3.426146 | 0.0012810 |
Marginal Effects for a Model with a Quadratic Term
Code
clr_spec <- linear_reg() %>%
set_engine("lm")
clr_rec <- recipe(y ~ x, data = my_data) %>%
step_poly(x, degree = 2, options = list(raw = TRUE))
clr_wf <- workflow() %>%
add_model(clr_spec) %>%
add_recipe(clr_rec)
clr_fit <- clr_wf %>%
fit(my_data)
clr_fit %>%
extract_fit_engine() %>%
tidy() %>%
kable() %>%
kable_styling(font_size = 16)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -23.7867692 | 7.0140682 | -3.391294 | 0.0014188 |
| x_poly_1 | 21.8554094 | 2.9863758 | 7.318372 | 0.0000000 |
| x_poly_2 | -0.9402959 | 0.2744471 | -3.426146 | 0.0012810 |
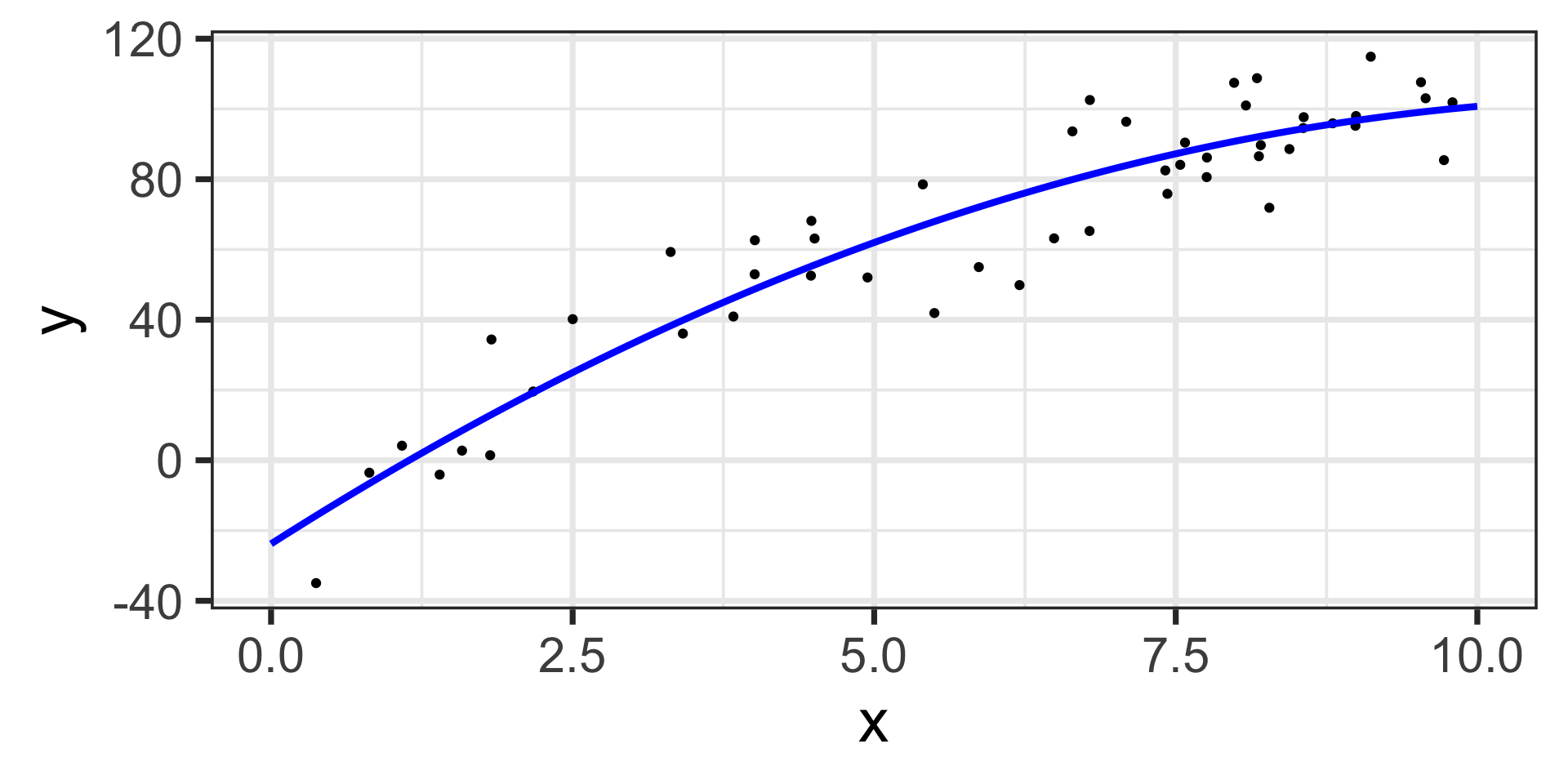
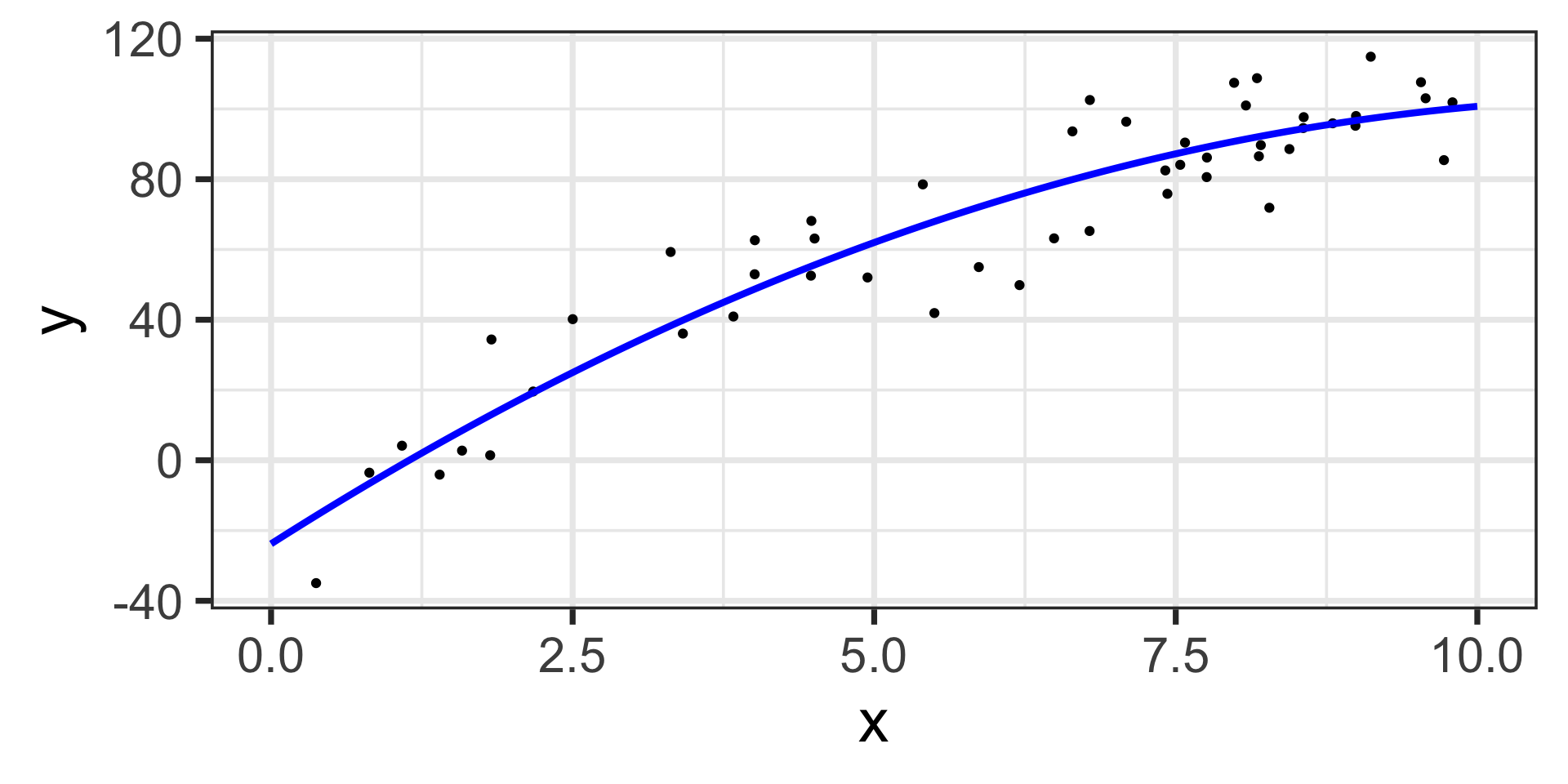
\[\mathbb{E}\left[y\right] = -23.79 + 21.86\cdot x - 0.94\cdot x^2\]
The estimated model appears below, on top of the training data.
Marginal Effects for a Model with a Quadratic Term
Code
clr_spec <- linear_reg() %>%
set_engine("lm")
clr_rec <- recipe(y ~ x, data = my_data) %>%
step_poly(x, degree = 2, options = list(raw = TRUE))
clr_wf <- workflow() %>%
add_model(clr_spec) %>%
add_recipe(clr_rec)
clr_fit <- clr_wf %>%
fit(my_data)
clr_fit %>%
extract_fit_engine() %>%
tidy() %>%
kable() %>%
kable_styling(font_size = 16)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -23.7867692 | 7.0140682 | -3.391294 | 0.0014188 |
| x_poly_1 | 21.8554094 | 2.9863758 | 7.318372 | 0.0000000 |
| x_poly_2 | -0.9402959 | 0.2744471 | -3.426146 | 0.0012810 |
\[\mathbb{E}\left[y\right] = -23.79 + 21.86\cdot x - 0.94\cdot x^2\]
The estimated model appears below, on top of the training data.
Marginal Effects for a Model with a Quadratic Term
Code
clr_spec <- linear_reg() %>%
set_engine("lm")
clr_rec <- recipe(y ~ x, data = my_data) %>%
step_poly(x, degree = 2, options = list(raw = TRUE))
clr_wf <- workflow() %>%
add_model(clr_spec) %>%
add_recipe(clr_rec)
clr_fit <- clr_wf %>%
fit(my_data)
clr_fit %>%
extract_fit_engine() %>%
tidy() %>%
kable() %>%
kable_styling(font_size = 16)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -23.7867692 | 7.0140682 | -3.391294 | 0.0014188 |
| x_poly_1 | 21.8554094 | 2.9863758 | 7.318372 | 0.0000000 |
| x_poly_2 | -0.9402959 | 0.2744471 | -3.426146 | 0.0012810 |
\[\mathbb{E}\left[y\right] = -23.79 + 21.86\cdot x - 0.94\cdot x^2\]
The estimated model appears below, on top of the training data.
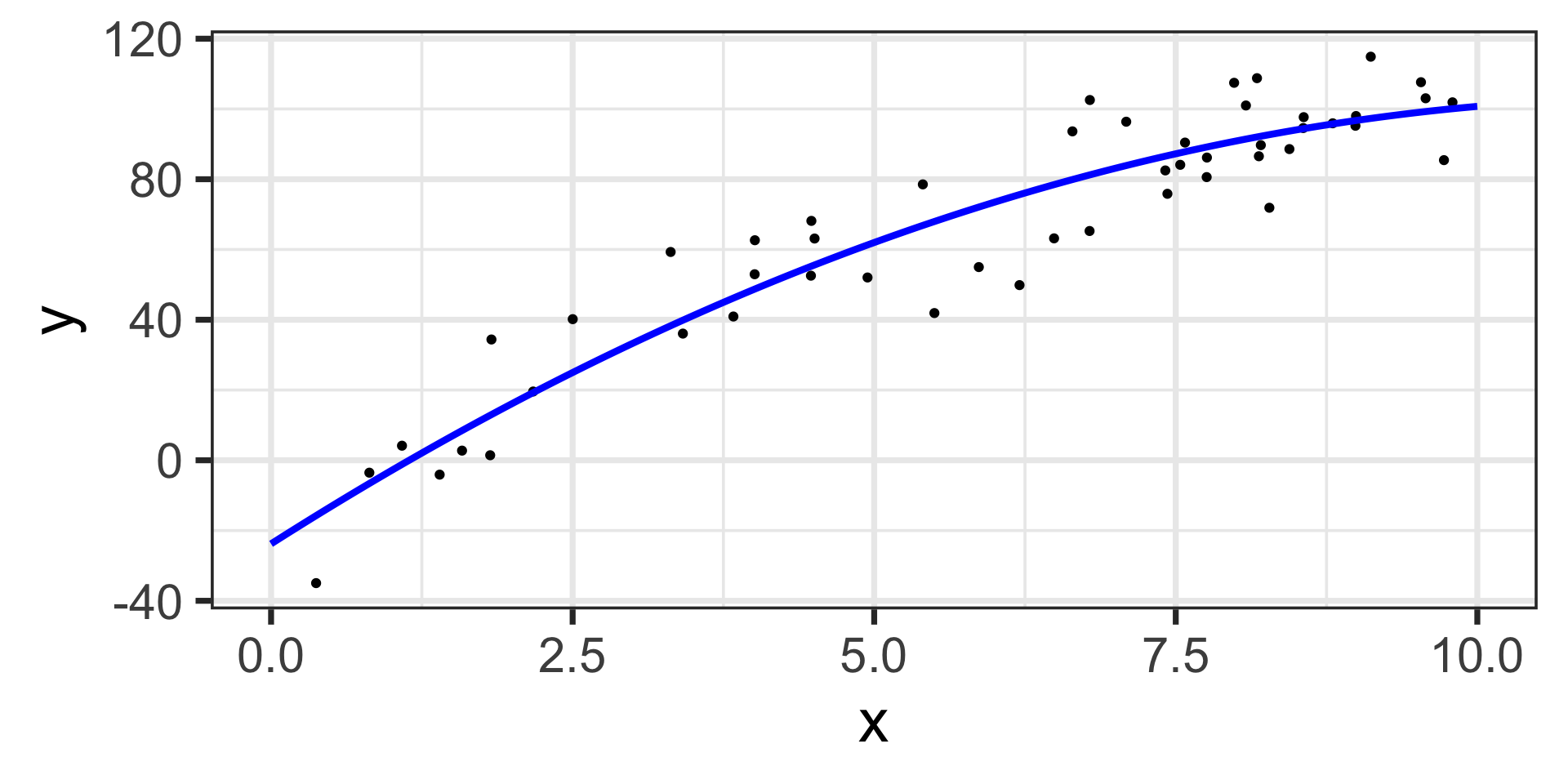
Now that we have our model, let’s use {marginaleffects} to determine the marginal effect of \(x\) on \(y\)
Marginal Effects for a Model with a Quadratic Term
Code
clr_spec <- linear_reg() %>%
set_engine("lm")
clr_rec <- recipe(y ~ x, data = my_data) %>%
step_poly(x, degree = 2, options = list(raw = TRUE))
clr_wf <- workflow() %>%
add_model(clr_spec) %>%
add_recipe(clr_rec)
clr_fit <- clr_wf %>%
fit(my_data)
clr_fit %>%
extract_fit_engine() %>%
tidy() %>%
kable() %>%
kable_styling(font_size = 16)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -23.7867692 | 7.0140682 | -3.391294 | 0.0014188 |
| x_poly_1 | 21.8554094 | 2.9863758 | 7.318372 | 0.0000000 |
| x_poly_2 | -0.9402959 | 0.2744471 | -3.426146 | 0.0012810 |
\[\mathbb{E}\left[y\right] = -23.79 + 21.86\cdot x - 0.94\cdot x^2\]
The estimated model appears below, on top of the training data.
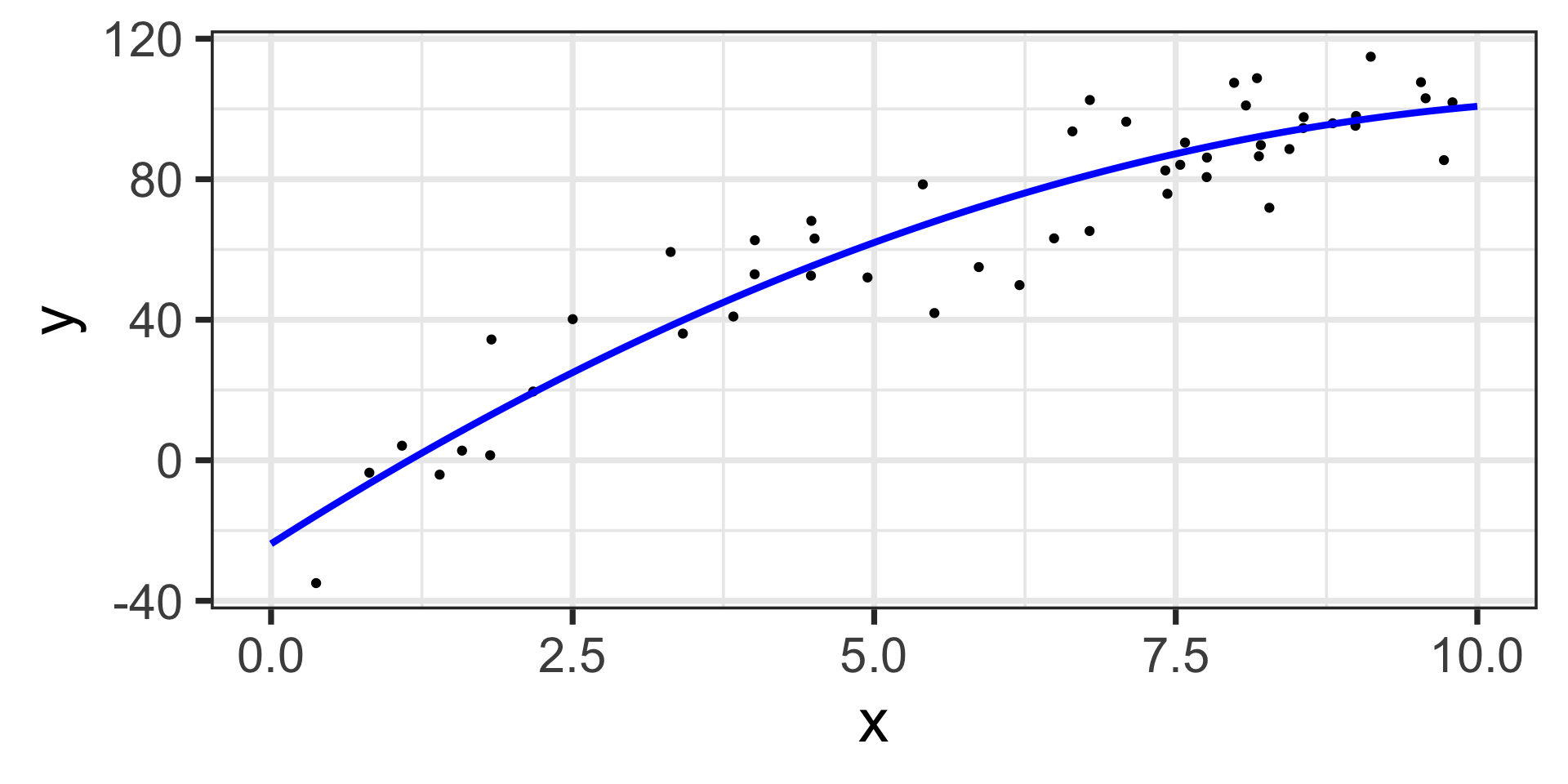
Now that we have our model, let’s use {marginaleffects} to determine the marginal effect of \(x\) on \(y\)
Code
mfx <- slopes(clr_fit,
newdata = my_data,
variable = "x") %>%
tibble() %>%
mutate(x = my_data$x)
mfx %>%
ggplot() +
geom_ribbon(aes(x = x,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x,
y = estimate),
color = "black",
linetype = "dashed") +
labs(x = "x",
y = "Marginal Effect of x on y") +
theme_bw(base_size = 24)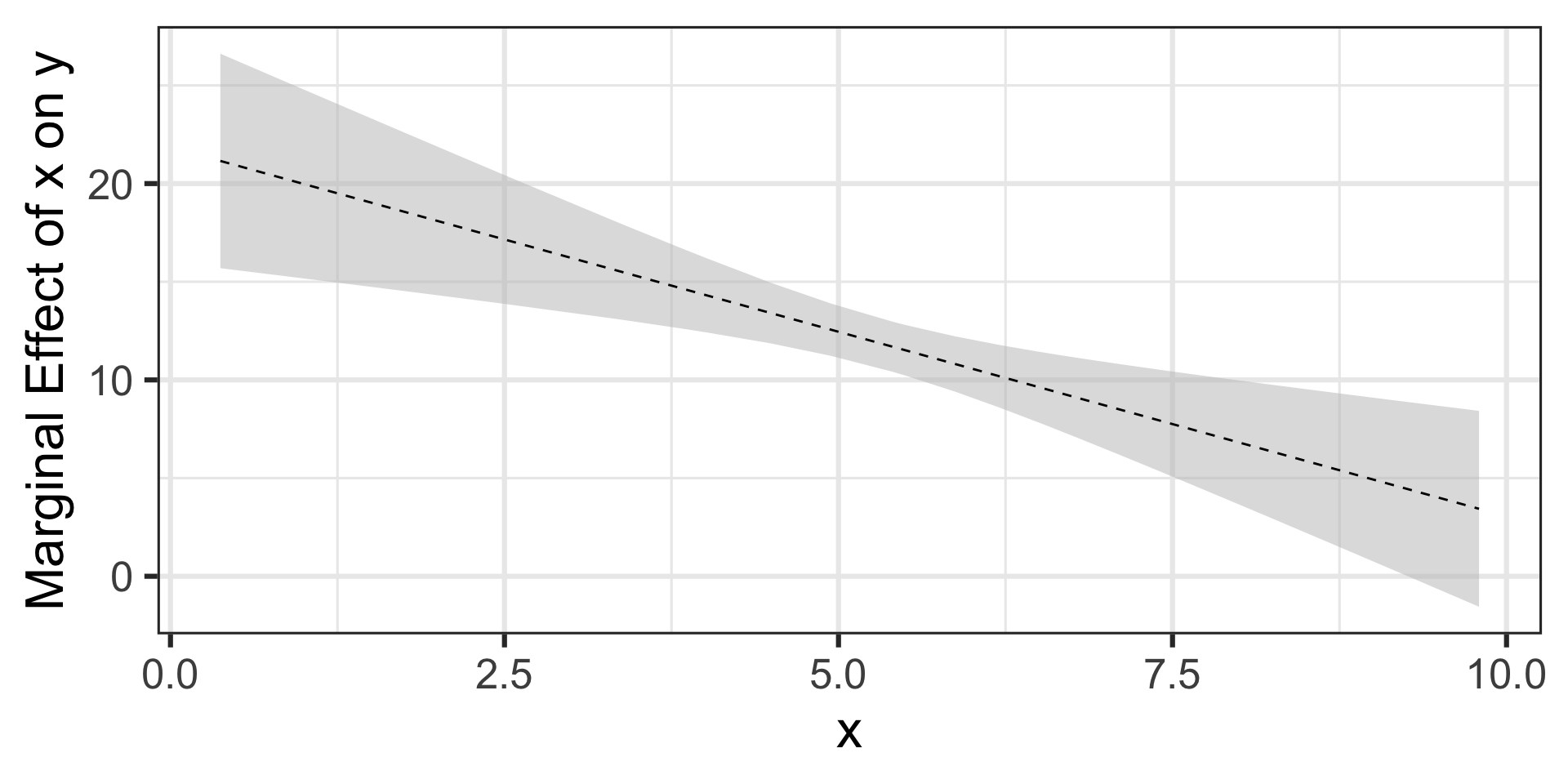
Marginal Effects for a Model with a Quadratic Term
Code
clr_spec <- linear_reg() %>%
set_engine("lm")
clr_rec <- recipe(y ~ x, data = my_data) %>%
step_poly(x, degree = 2, options = list(raw = TRUE))
clr_wf <- workflow() %>%
add_model(clr_spec) %>%
add_recipe(clr_rec)
clr_fit <- clr_wf %>%
fit(my_data)
clr_fit %>%
extract_fit_engine() %>%
tidy() %>%
kable() %>%
kable_styling(font_size = 16)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -23.7867692 | 7.0140682 | -3.391294 | 0.0014188 |
| x_poly_1 | 21.8554094 | 2.9863758 | 7.318372 | 0.0000000 |
| x_poly_2 | -0.9402959 | 0.2744471 | -3.426146 | 0.0012810 |
\[\mathbb{E}\left[y\right] = -23.79 + 21.86\cdot x - 0.94\cdot x^2\]
The estimated model appears below, on top of the training data.
The marginal effect of \(x\) on \(y\) varies with the value of \(x\) – we can compute it using the expression \(\beta_1 + 2x\beta_2\)
Now that we have our model, let’s use {marginaleffects} to determine the marginal effect of \(x\) on \(y\)
Code
mfx <- slopes(clr_fit,
newdata = my_data,
variable = "x") %>%
tibble() %>%
mutate(x = my_data$x)
mfx %>%
ggplot() +
geom_ribbon(aes(x = x,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x,
y = estimate),
color = "black",
linetype = "dashed") +
labs(x = "x",
y = "Marginal Effect of x on y") +
theme_bw(base_size = 24)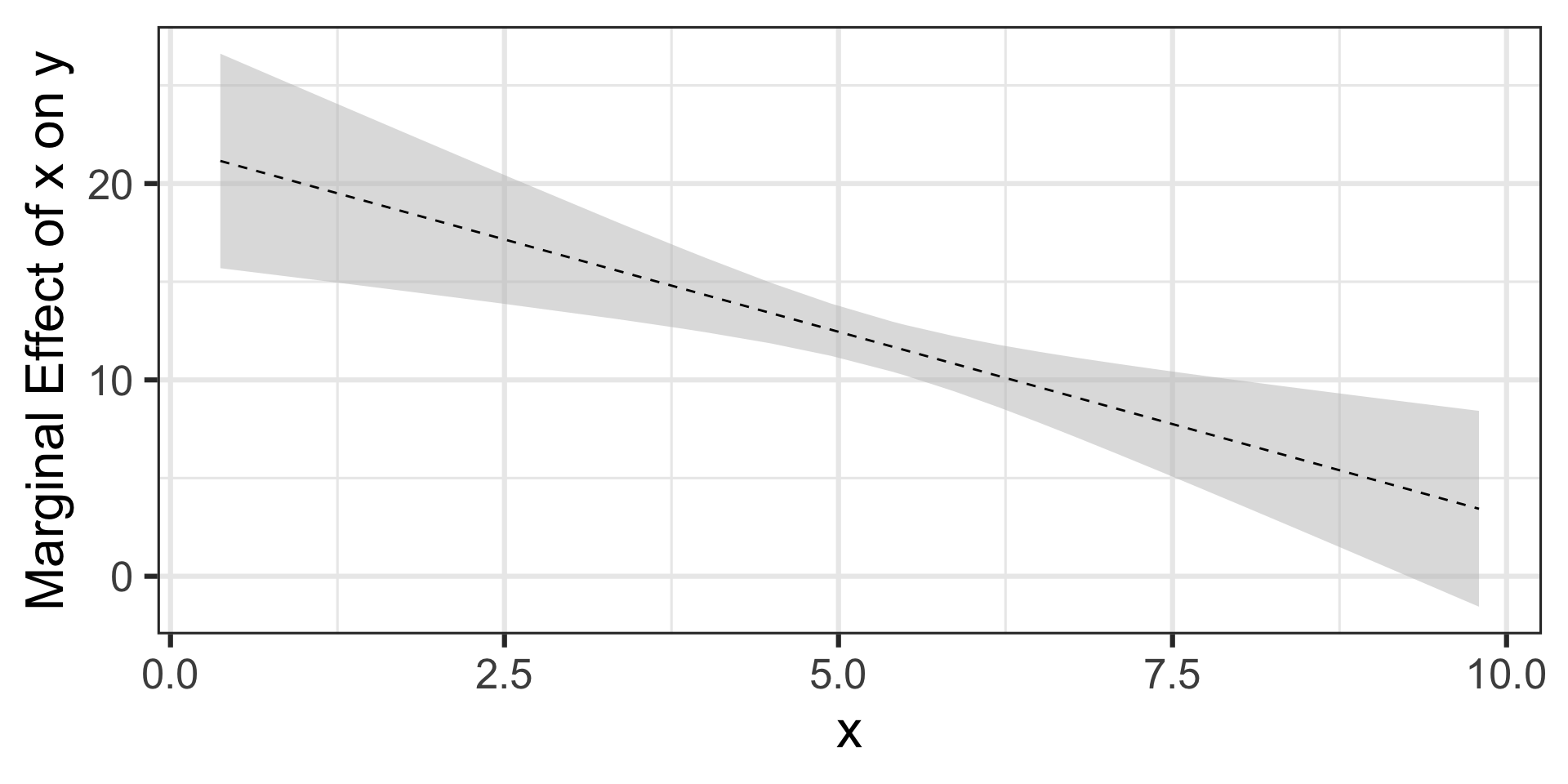
Marginal Effects for a Model with a Fifth-Degree Term
\[\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_3 x^3 + \beta_4 x^4 + \beta_5 x^5\]
The effect of a unit increase in \(x\) here will be an expected increase in \(y\) of about \(\beta_1 + 2x\beta_2 + 3x^2\beta_3 + 4x^3\beta_4 + 5x^4\beta_5\)
Let’s see what {marginaleffects} does for us now…
Marginal Effects for a Model with a Fifth-Degree Term
Code
c5lr_spec <- linear_reg() %>%
set_engine("lm")
c5lr_rec <- recipe(y ~ x, data = my_data) %>%
step_poly(x, degree = 5, options = list(raw = TRUE))
c5lr_wf <- workflow() %>%
add_model(c5lr_spec) %>%
add_recipe(c5lr_rec)
c5lr_fit <- c5lr_wf %>%
fit(my_data)
c5lr_fit %>%
extract_fit_engine() %>%
tidy() %>%
kable() %>%
kable_styling(font_size = 18)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 1456.42853 | 87.2770015 | 16.687426 | 0 |
| x_poly_1 | -2656.06576 | 203.9694258 | -13.021882 | 0 |
| x_poly_2 | 1471.67063 | 127.7291663 | 11.521806 | 0 |
| x_poly_3 | -342.63961 | 32.3272653 | -10.599090 | 0 |
| x_poly_4 | 35.03516 | 3.5639283 | 9.830489 | 0 |
| x_poly_5 | -1.29421 | 0.1421908 | -9.101923 | 0 |
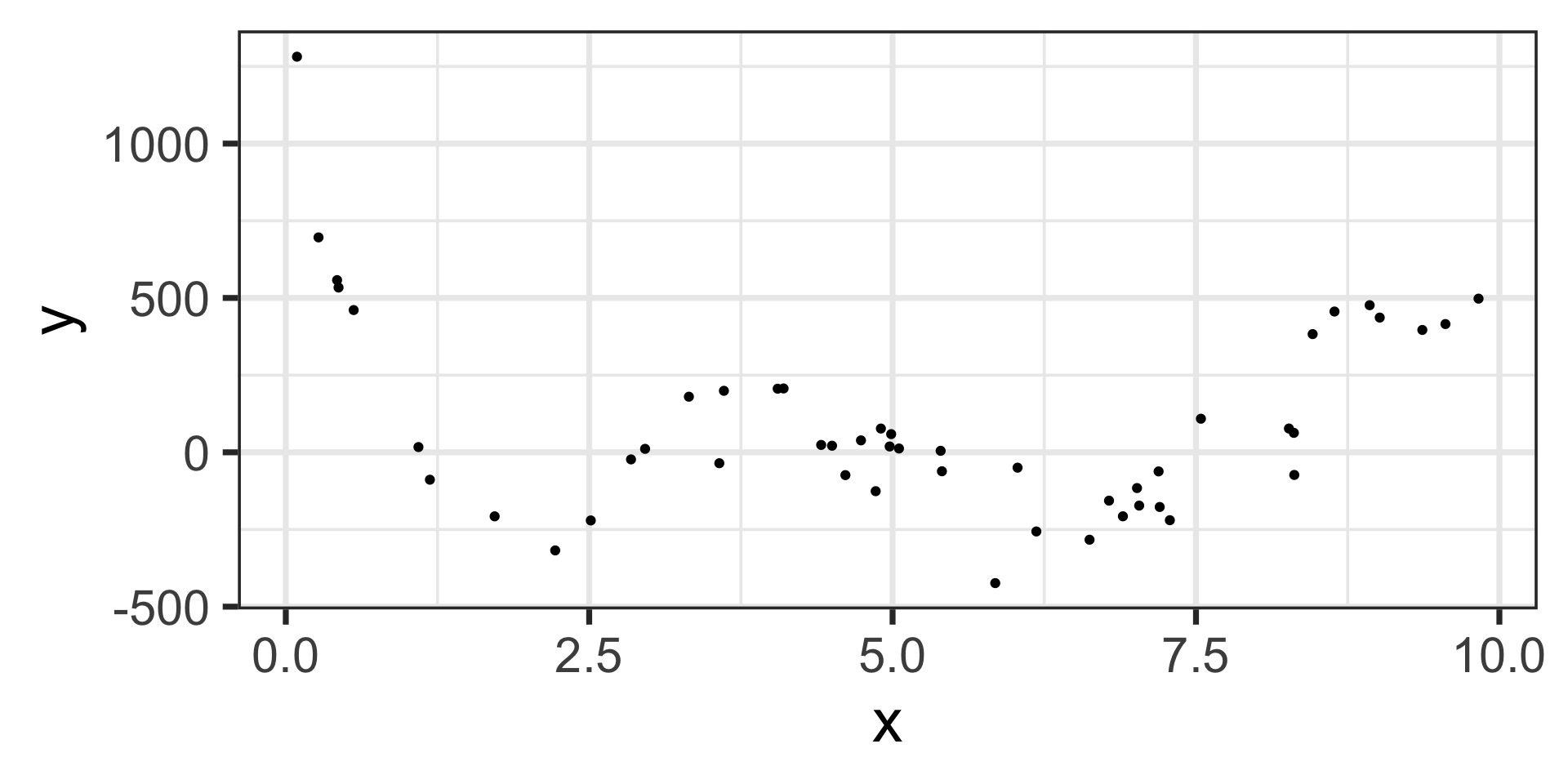
\[\mathbb{E}\left[y\right] = 1456.43 - 2656.07\cdot x + 1471.67\cdot x^2 - 342.64\cdot x^3 + 35.03\cdot x^4 - 1.29\cdot x^5\]
Marginal Effects for a Model with a Fifth-Degree Term
\[\mathbb{E}\left[y\right] = 1456.43 - 2656.07\cdot x + 1471.67\cdot x^2 - 342.64\cdot x^3 + 35.03\cdot x^4 - 1.29\cdot x^5\]
The estimated model appears below, on top of the training data.
Marginal Effects for a Model with a Fifth-Degree Term
\[\mathbb{E}\left[y\right] = 1456.43 - 2656.07\cdot x + 1471.67\cdot x^2 - 342.64\cdot x^3 + 35.03\cdot x^4 - 1.29\cdot x^5\]
The estimated model appears below, on top of the training data.
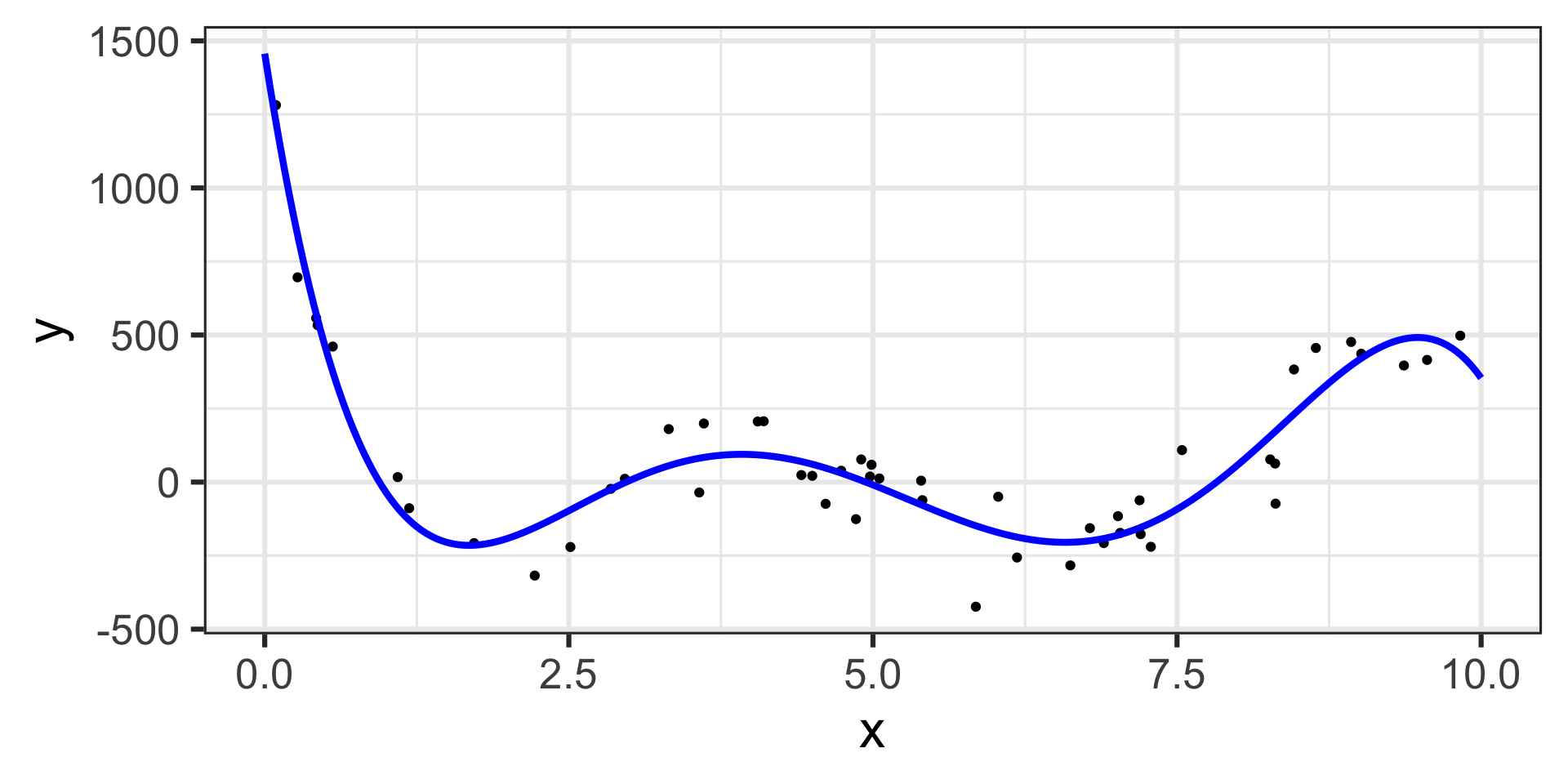
Marginal Effects for a Model with a Fifth-Degree Term
\[\mathbb{E}\left[y\right] = 1456.43 - 2656.07\cdot x + 1471.67\cdot x^2 - 342.64\cdot x^3 + 35.03\cdot x^4 - 1.29\cdot x^5\]
The estimated model appears below, on top of the training data.
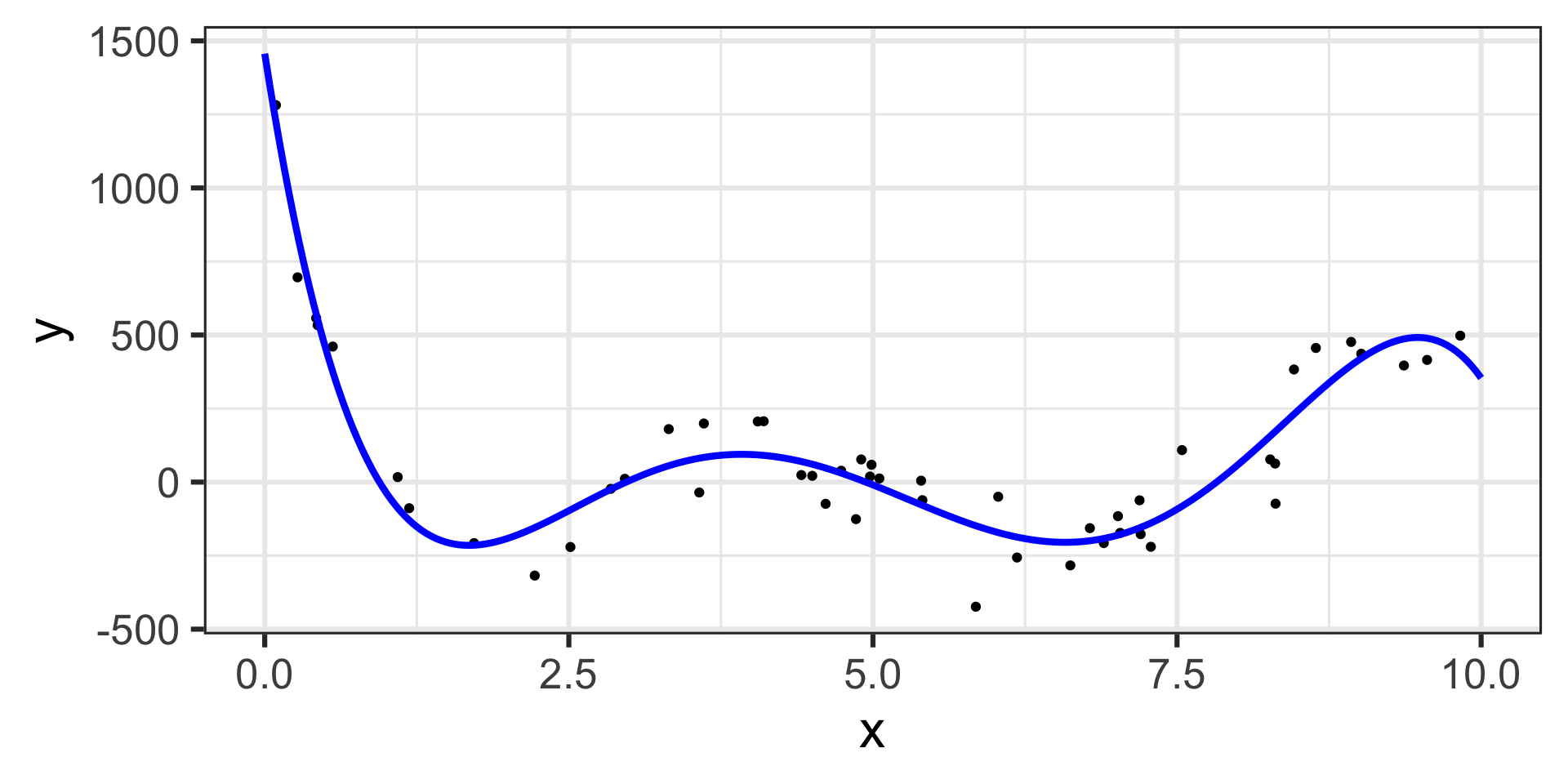
Now we’ll call on {marginaleffects}
Marginal Effects for a Model with a Fifth-Degree Term
\[\mathbb{E}\left[y\right] = 1456.43 - 2656.07\cdot x + 1471.67\cdot x^2 - 342.64\cdot x^3 + 35.03\cdot x^4 - 1.29\cdot x^5\]
The estimated model appears below, on top of the training data.
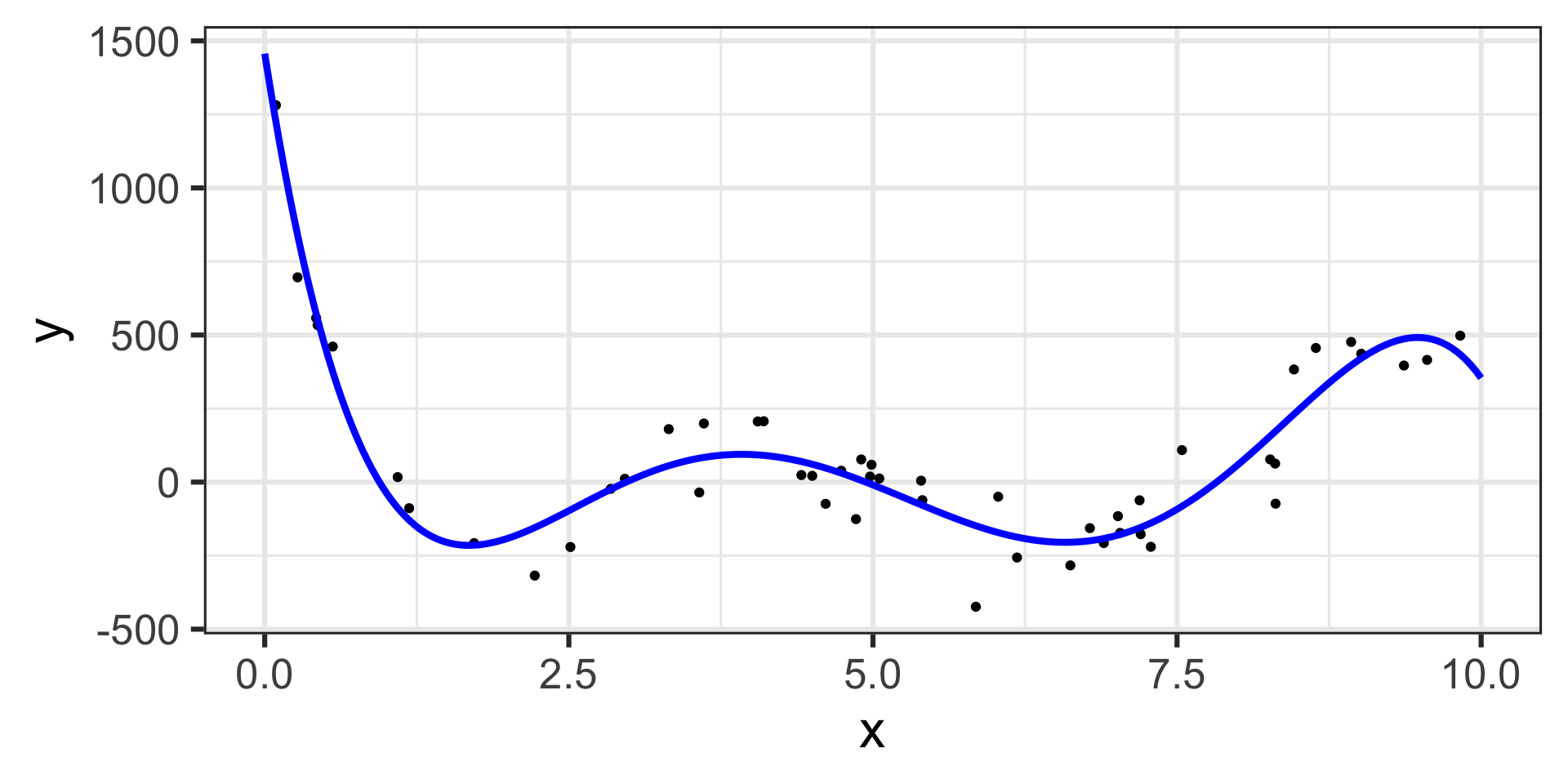
Now we’ll call on {marginaleffects}
Code
mfx <- slopes(c5lr_fit,
newdata = my_data,
variable = "x") %>%
tibble() %>%
mutate(x = my_data$x)
mfx %>%
ggplot() +
geom_ribbon(aes(x = x,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x,
y = estimate),
color = "black",
linetype = "dashed") +
labs(x = "x",
y = "Marginal Effect of x on y") +
theme_bw(base_size = 26)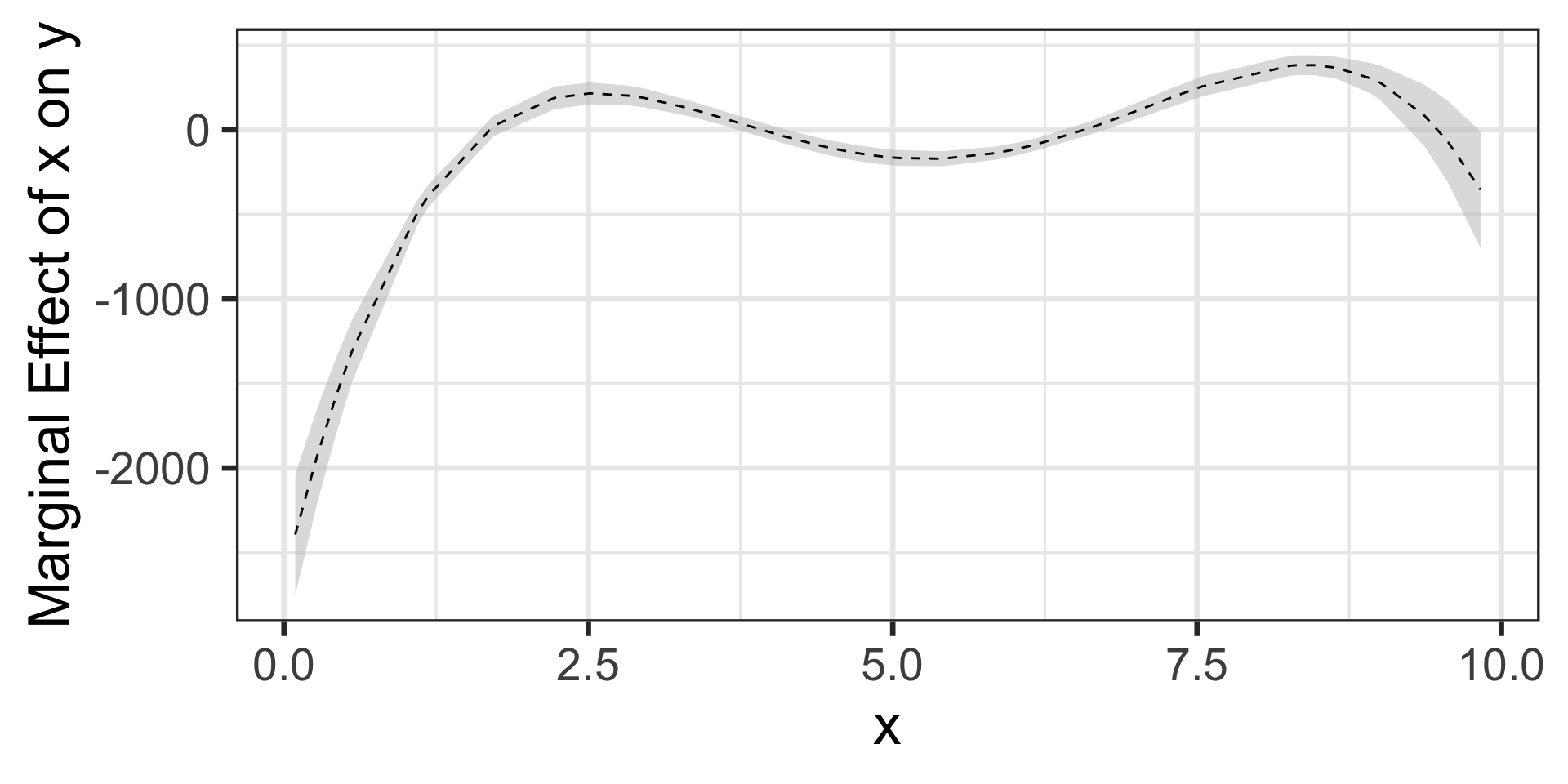
As in the case of the quadratic model we can see that the marginal effect of \(x\) on the response changes.
That is, the marginal effect of \(x\) on \(y\) depends on the “current” value of \(x\).
Marginal Effects for a Model with Linear Interactions
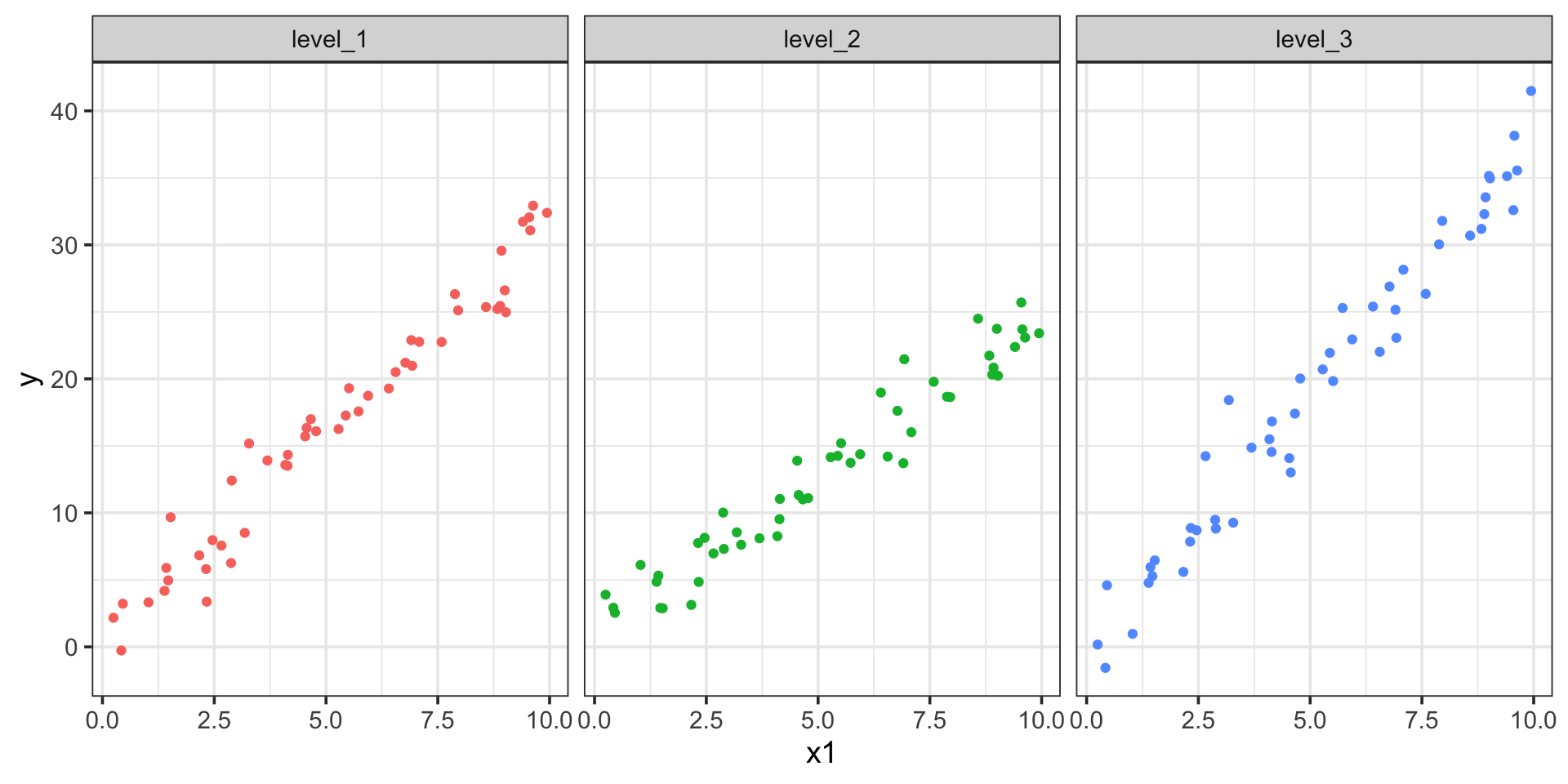
\[\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x_1 + \beta_2\cdot\left(\text{level 2}\right) + \beta_3\cdot\left(\text{level 3}\right) + \beta_4\cdot x_1\left(\text{level 2}\right) + \beta_5\cdot x_1\left(\text{level 3}\right)\]
Here, we know that the effect of a unit increase in \(x_1\) depends on the observed level of \(x_2\)
That is, the marginal effect of \(x_1\) on \(y\) depends on the level of \(x_2\) – let’s see what {marginaleffects} gives us
Marginal Effects for a Model with Linear Interactions
Code
lr_spec <- linear_reg() %>%
set_engine("lm")
lr_rec <- recipe(y ~ ., data = my_data) %>%
step_dummy(x2) %>%
step_interact(~ x1:starts_with("x2"))
lr_wf <- workflow() %>%
add_model(lr_spec) %>%
add_recipe(lr_rec)
lr_fit <- lr_wf %>%
fit(my_data)
lr_fit %>%
extract_fit_engine() %>%
tidy() %>%
kable() %>%
kable_styling(font_size = 18)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.7152946 | 0.5626705 | 1.2712495 | 0.2056895 |
| x1 | 3.0763489 | 0.0943876 | 32.5927234 | 0.0000000 |
| x2_level_2 | 0.4670825 | 0.7957363 | 0.5869816 | 0.5581352 |
| x2_level_3 | -1.0413289 | 0.7957363 | -1.3086357 | 0.1927425 |
| x1_x_x2_level_2 | -0.7641695 | 0.1334842 | -5.7247929 | 0.0000001 |
| x1_x_x2_level_3 | 0.7333109 | 0.1334842 | 5.4936145 | 0.0000002 |
\[\mathbb{E}\left[y\right] = 0.72 + 3.08\cdot x_1 + 0.47\cdot \texttt{level2} - 1.04\cdot\texttt{level3} -0.76\cdot x_1\cdot\texttt{level2} + 0.73\cdot x_1\cdot\texttt{level3}\]
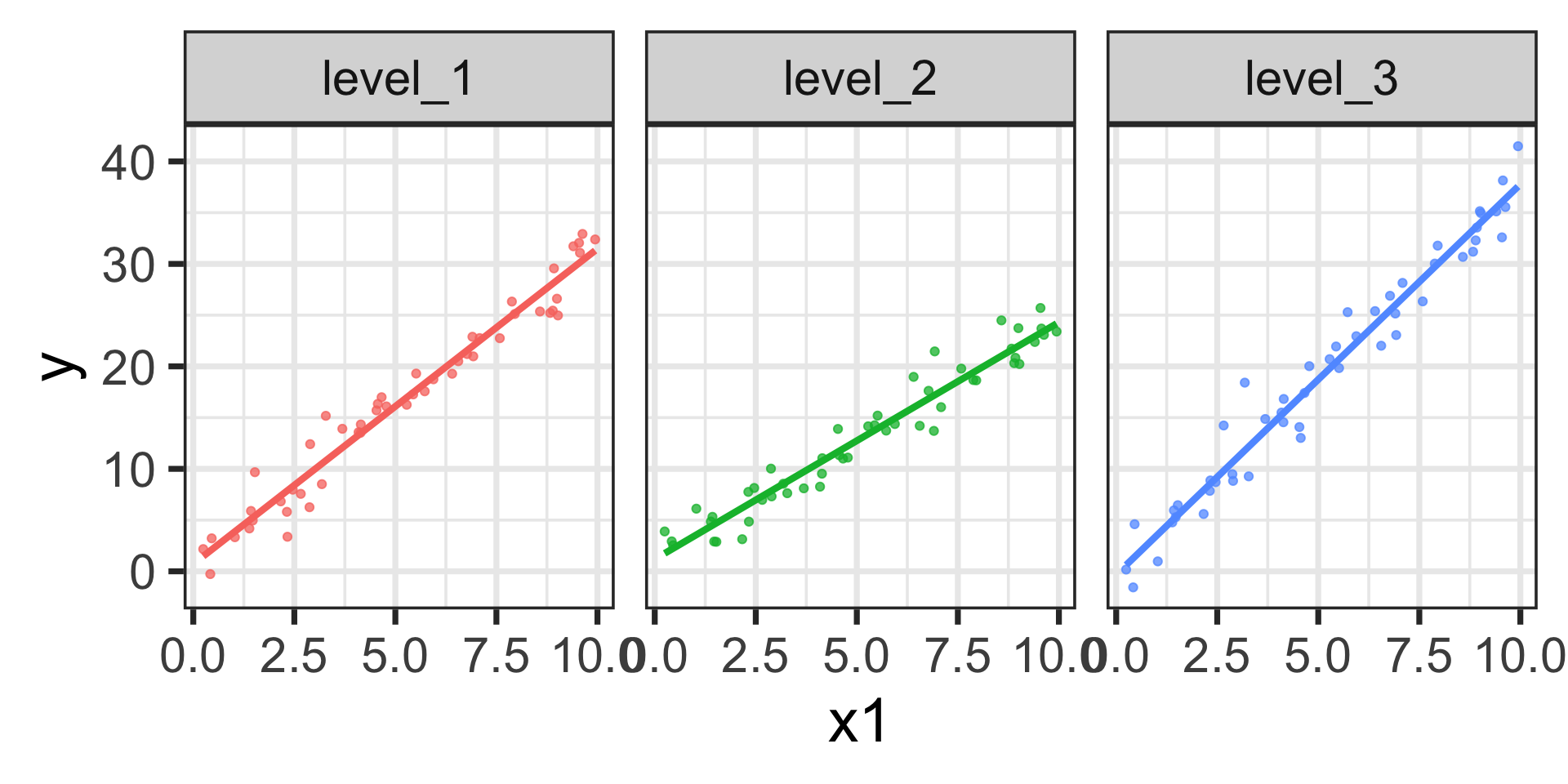
Marginal Effects for a Model with Linear Interactions
\[\mathbb{E}\left[y\right] = 0.72 + 3.08\cdot x_1 + 0.47\cdot \texttt{level2} - 1.04\cdot\texttt{level3} -0.76\cdot x_1\cdot\texttt{level2} + 0.73\cdot x_1\cdot\texttt{level3}\]
The estimated models are shown below.
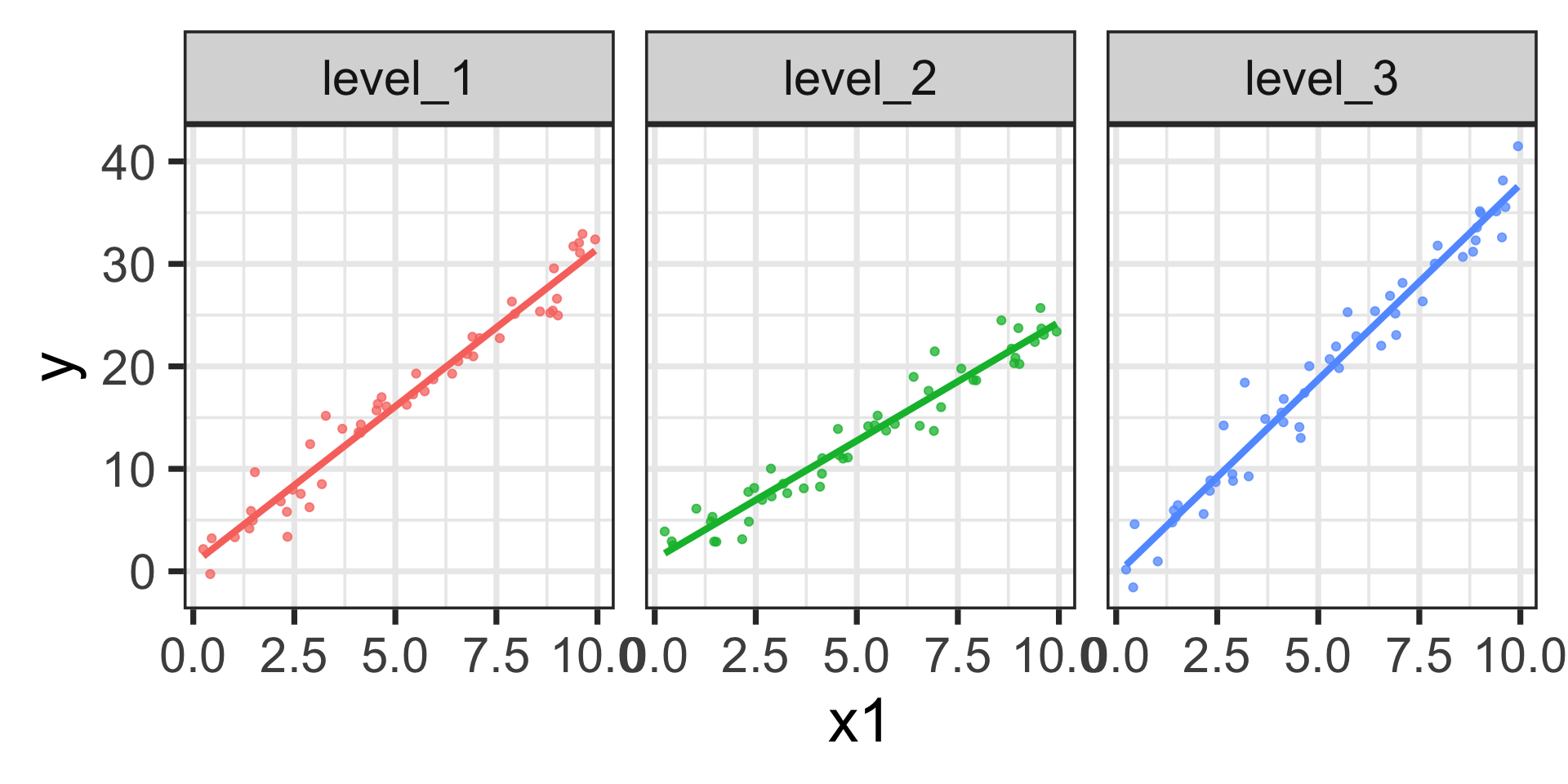
Marginal Effects for a Model with Linear Interactions
\[\mathbb{E}\left[y\right] = 0.72 + 3.08\cdot x_1 + 0.47\cdot \texttt{level2} - 1.04\cdot\texttt{level3} -0.76\cdot x_1\cdot\texttt{level2} + 0.73\cdot x_1\cdot\texttt{level3}\]
The estimated models are shown below.
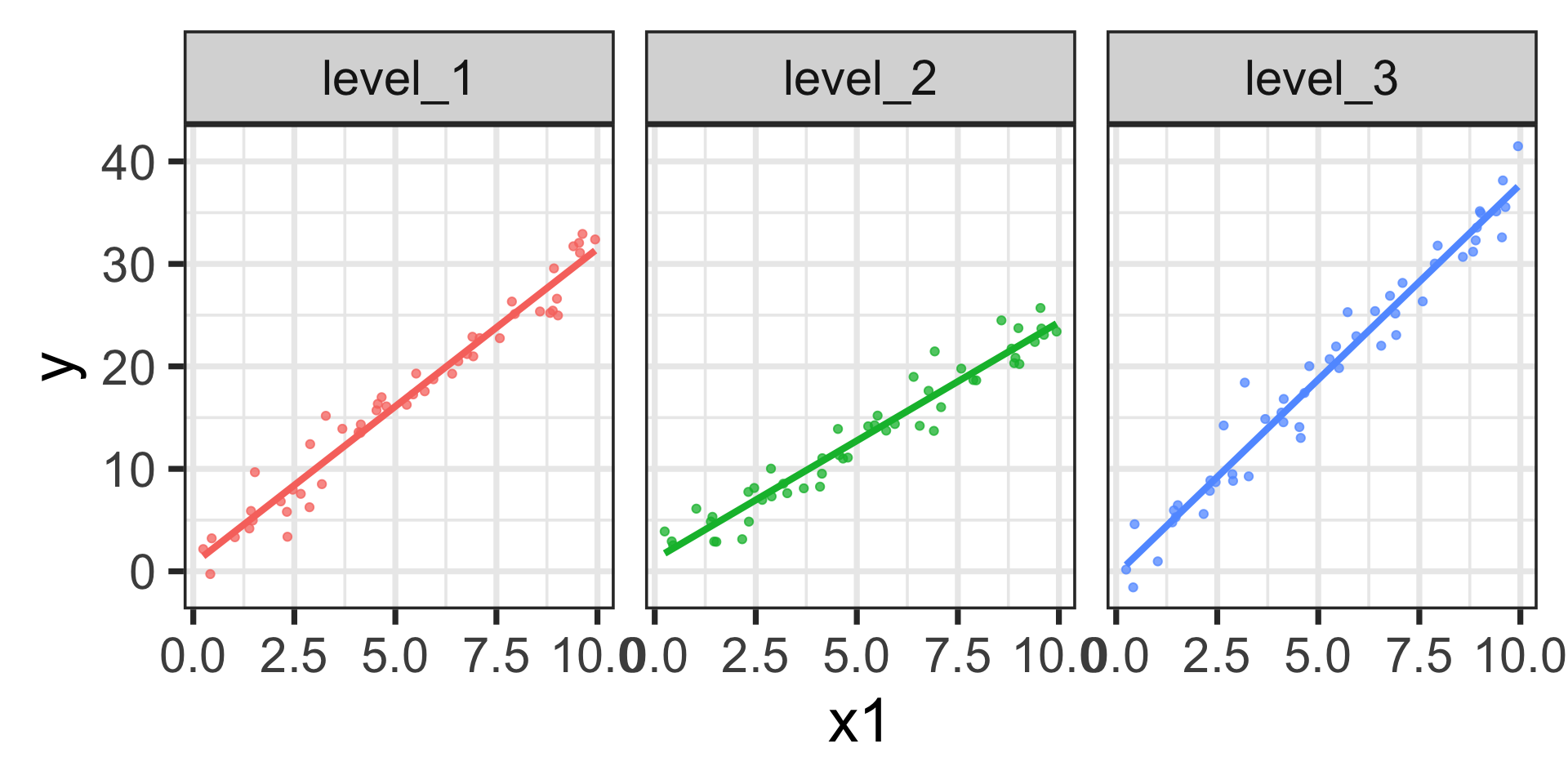
Marginal Effects for a Model with Linear Interactions
\[\mathbb{E}\left[y\right] = 0.72 + 3.08\cdot x_1 + 0.47\cdot \texttt{level2} - 1.04\cdot\texttt{level3} -0.76\cdot x_1\cdot\texttt{level2} + 0.73\cdot x_1\cdot\texttt{level3}\]
The estimated models are shown below.
Let’s check on the marginal effects with {marginaleffects}
Marginal Effects for a Model with Linear Interactions
\[\mathbb{E}\left[y\right] = 0.72 + 3.08\cdot x_1 + 0.47\cdot \texttt{level2} - 1.04\cdot\texttt{level3} -0.76\cdot x_1\cdot\texttt{level2} + 0.73\cdot x_1\cdot\texttt{level3}\]
The estimated models are shown below.
Let’s check on the marginal effects with {marginaleffects}
Code
mfx <- slopes(lr_fit,
newdata = my_data,
variable = "x1") %>%
tibble() %>%
mutate(x1 = my_data$x1,
x2 = my_data$x2)
mfx %>%
ggplot() +
geom_ribbon(aes(x = x1,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x1,
y = estimate),
color = "black",
linetype = "dashed") +
labs(x = "x1",
y = "Marginal Effect of x1 on y") +
facet_wrap(~x2) +
theme_bw(base_size = 28)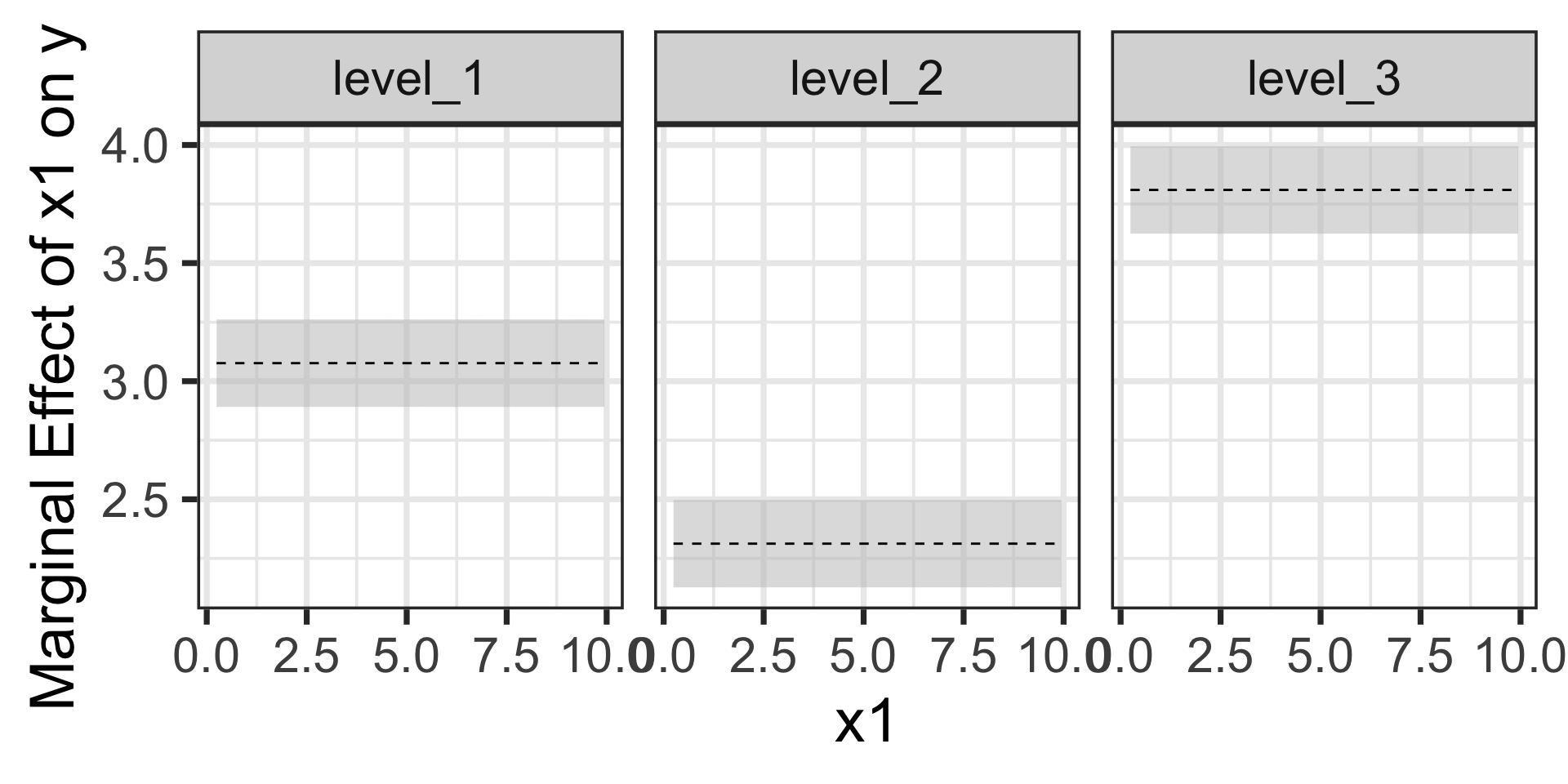
Marginal Effects for a Model with Linear Interactions
\[\mathbb{E}\left[y\right] = 0.72 + 3.08\cdot x_1 + 0.47\cdot \texttt{level2} - 1.04\cdot\texttt{level3} -0.76\cdot x_1\cdot\texttt{level2} + 0.73\cdot x_1\cdot\texttt{level3}\]
The estimated models are shown below.
We can see the differences in slopes (marginal effects) across the three levels of \(x_2\)
- level_1: \(\beta_1 \approx 3.08\)
- level_2: \(\beta_1 + \beta_4 \approx 3.08 - 0.76 = 2.32\)
- level_3: \(\beta_1 + \beta_5 \approx 3.08 + 0.73 = 3.81\)
Let’s check on the marginal effects with {marginaleffects}
Code
mfx <- slopes(lr_fit,
newdata = my_data,
variable = "x1") %>%
tibble() %>%
mutate(x1 = my_data$x1,
x2 = my_data$x2)
mfx %>%
ggplot() +
geom_ribbon(aes(x = x1,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x1,
y = estimate),
color = "black",
linetype = "dashed") +
labs(x = "x1",
y = "Marginal Effect of x1 on y") +
facet_wrap(~x2) +
theme_bw(base_size = 28)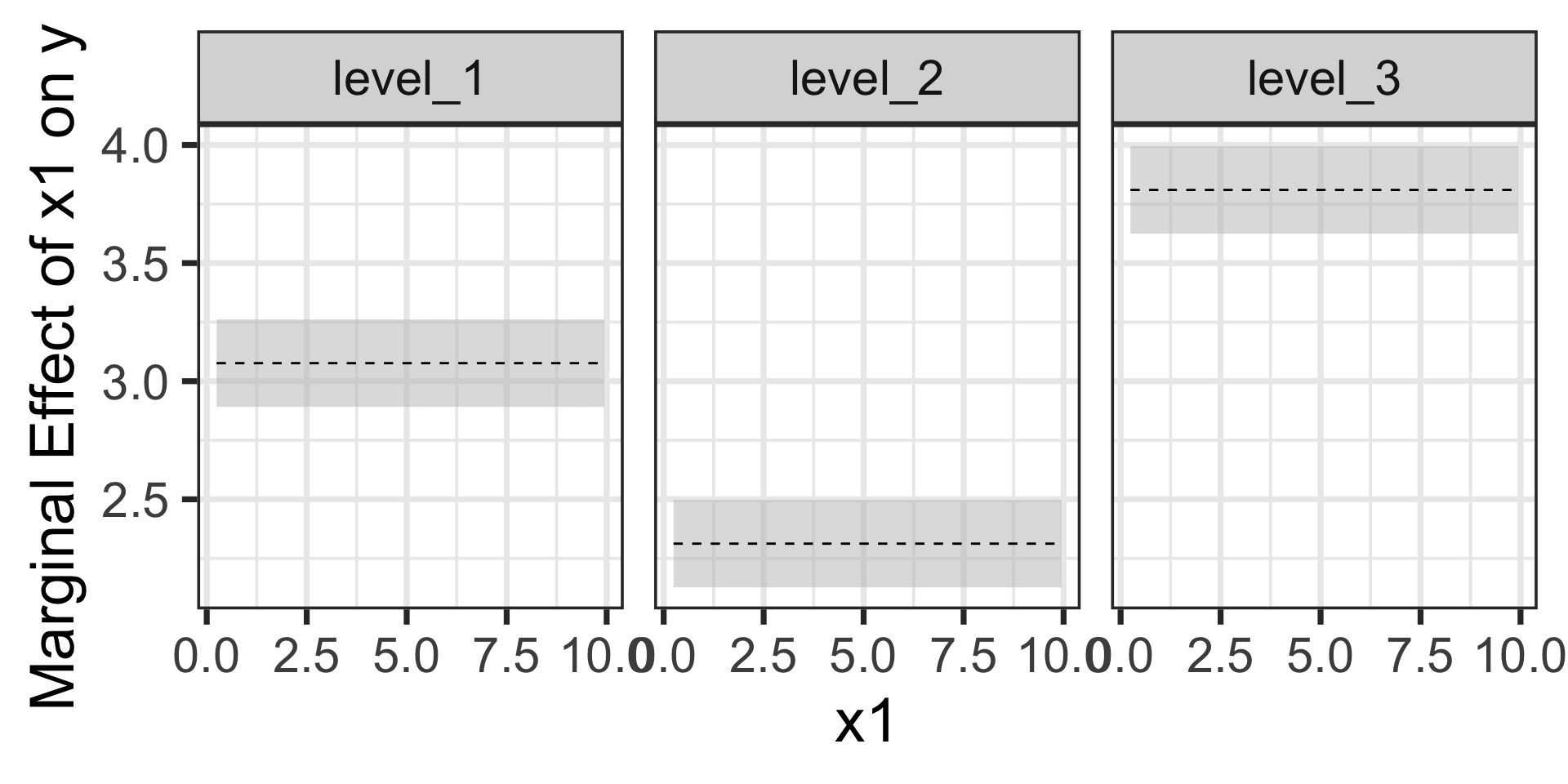
Marginal Effects for a Model with Curvi-Linear Interactions
\[\begin{align} \mathbb{E}\left[y\right] = \beta_0 +~ &\beta_1 x_1 + \beta_2 x_1^2 + \beta_3\cdot\left(\text{level 2}\right) + \beta_4\cdot\left(\text{level 3}\right) +\\ &\beta_5\cdot x_1\left(\text{level 2}\right) + \beta_6\cdot x_1\left(\text{level 3}\right) +\\ &\beta_7\cdot x_1^2\left(\text{level 2}\right) + \beta_8\cdot x_1^2\left(\text{level 3}\right)\end{align}\]
Let’s fit the model and see how {marginaleffects} helps us analyze the expected effect of a unit change in \(x_1\) across the different levels of \(x_2\)
Marginal Effects for a Model with Curvi-Linear Interactions
Code
lr_spec <- linear_reg() %>%
set_engine("lm")
lr_rec <- recipe(y ~ ., data = my_data) %>%
step_dummy(x2) %>%
step_poly(x1, degree = 2, options = list(raw = TRUE)) %>%
step_interact(~ starts_with("x1"):starts_with("x2"))
lr_wf <- workflow() %>%
add_model(lr_spec) %>%
add_recipe(lr_rec)
lr_fit <- lr_wf %>%
fit(my_data)
lr_fit %>%
extract_fit_engine() %>%
tidy() %>%
kable() %>%
kable_styling(font_size = 18)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -53.7668812 | 6.8006902 | -7.906092 | 0.0000000 |
| x2_level_2 | 65.4170016 | 9.6176284 | 6.801781 | 0.0000000 |
| x2_level_3 | 100.2164522 | 9.6176284 | 10.420079 | 0.0000000 |
| x1_poly_1 | 28.2837759 | 3.0215366 | 9.360726 | 0.0000000 |
| x1_poly_2 | -1.2701658 | 0.2803949 | -4.529918 | 0.0000125 |
| x1_poly_1_x_x2_level_2 | -11.1871027 | 4.2730980 | -2.618031 | 0.0098098 |
| x1_poly_1_x_x2_level_3 | -17.2247637 | 4.2730980 | -4.030978 | 0.0000905 |
| x1_poly_2_x_x2_level_2 | 0.4964708 | 0.3965383 | 1.252012 | 0.2126382 |
| x1_poly_2_x_x2_level_3 | 0.7117611 | 0.3965383 | 1.794937 | 0.0748059 |
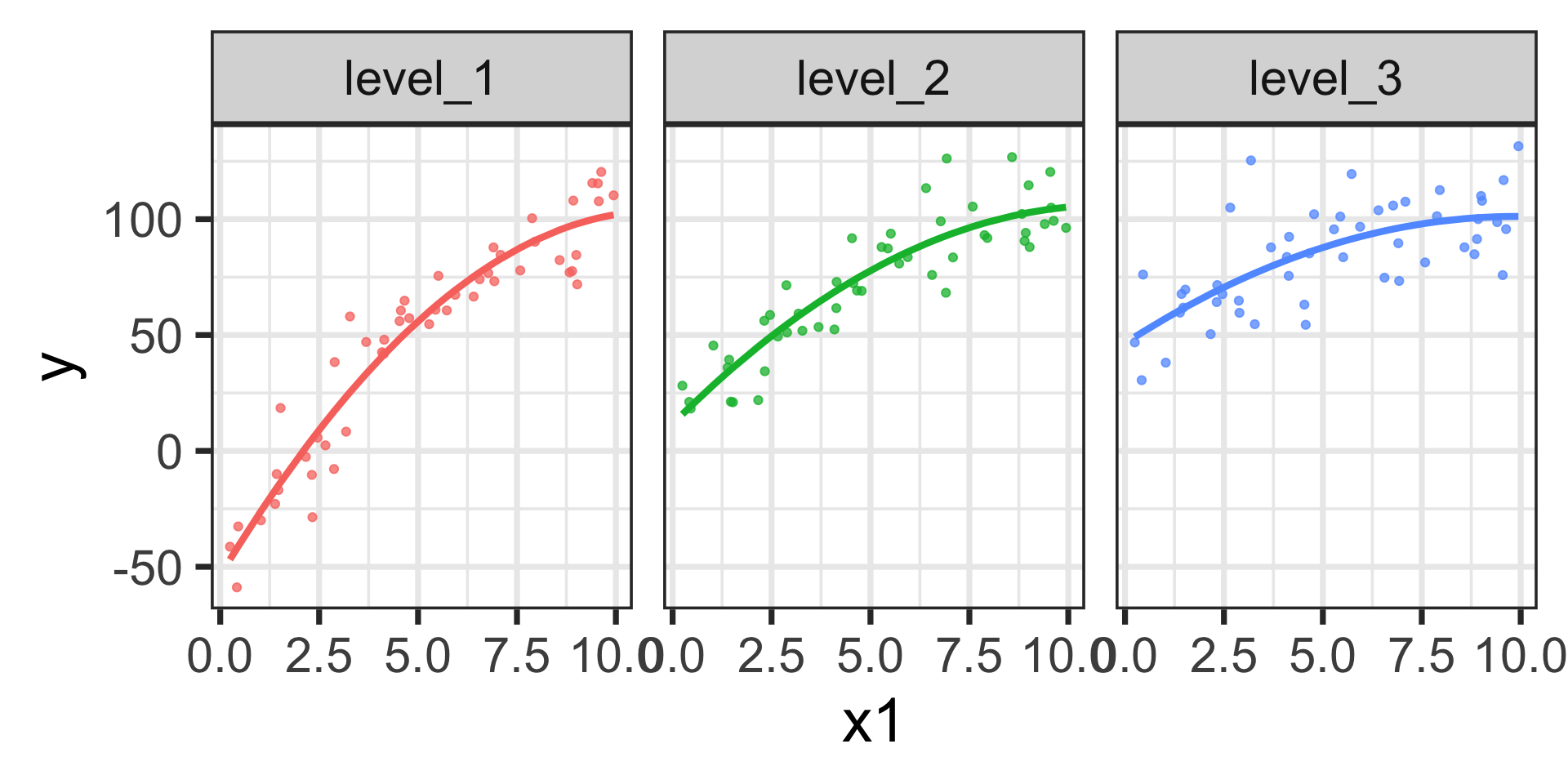
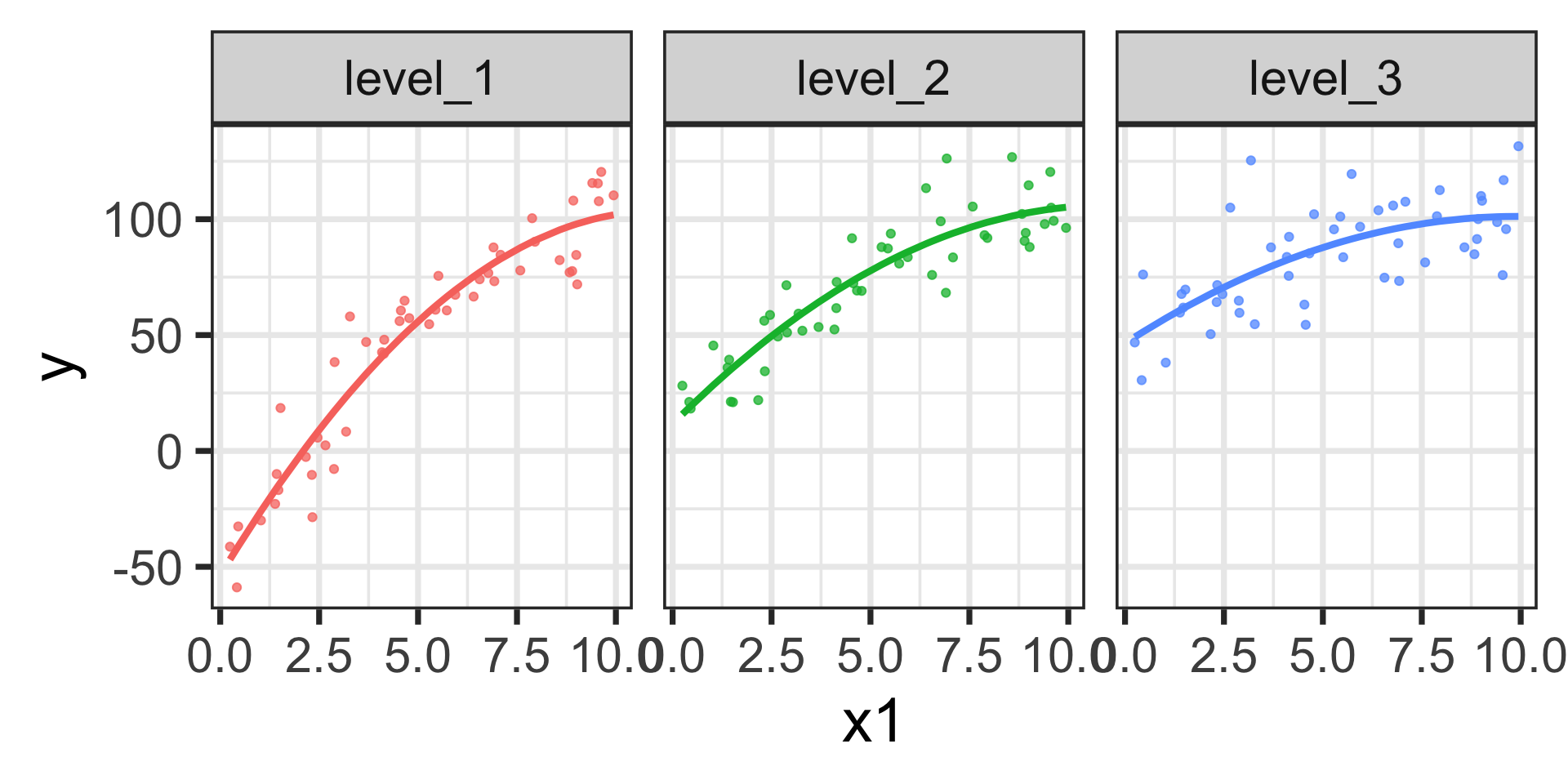
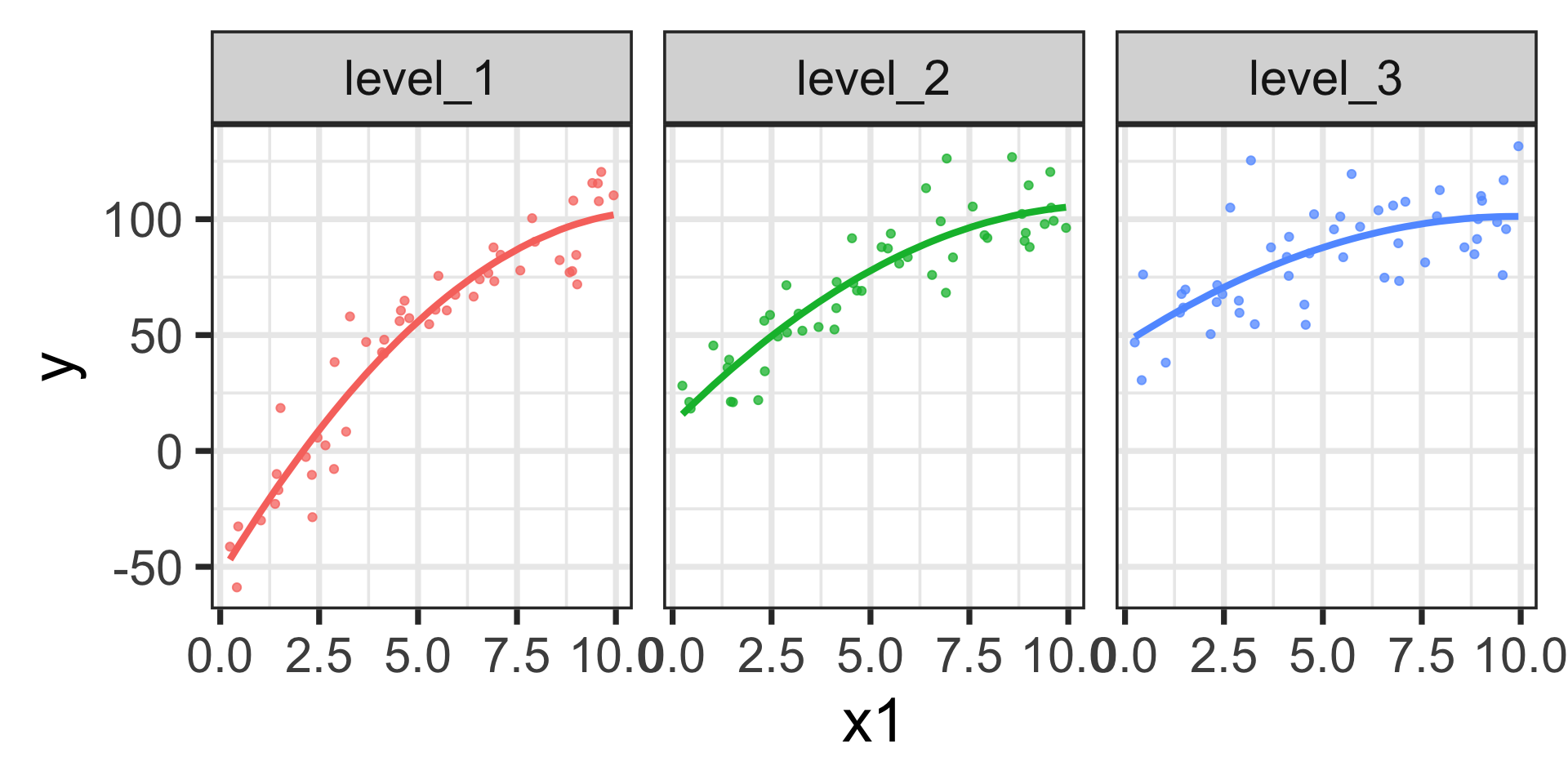
\[\begin{align} \mathbb{E}\left[y\right] = -53.77 +~ &28.28 x_1 - 1.27x_1^2 + 65.42\cdot\left(\text{level 2}\right) + 100.22\cdot\left(\text{level 3}\right) +\\ &-11.19\cdot x_1\left(\text{level 2}\right) - 17.22\cdot x_1\left(\text{level 3}\right) +\\ &0.50\cdot x_1^2\left(\text{level 2}\right) + 0.71\cdot x_1^2\left(\text{level 3}\right)\end{align}\]
Let’s check on the marginal effects with {marginaleffects}
Marginal Effects for a Model with Curvi-Linear Interactions
\[\begin{align} \mathbb{E}\left[y\right] = -53.77 +~ &28.28 x_1 - 1.27x_1^2 + 65.42\cdot\left(\text{level 2}\right) + 100.22\cdot\left(\text{level 3}\right) +\\ &-11.19\cdot x_1\left(\text{level 2}\right) - 17.22\cdot x_1\left(\text{level 3}\right) +\\ &0.50\cdot x_1^2\left(\text{level 2}\right) + 0.71\cdot x_1^2\left(\text{level 3}\right)\end{align}\]
Again, the estimated models are shown below.
Marginal Effects for a Model with Curvi-Linear Interactions
\[\begin{align} \mathbb{E}\left[y\right] = -53.77 +~ &28.28 x_1 - 1.27x_1^2 + 65.42\cdot\left(\text{level 2}\right) + 100.22\cdot\left(\text{level 3}\right) +\\ &-11.19\cdot x_1\left(\text{level 2}\right) - 17.22\cdot x_1\left(\text{level 3}\right) +\\ &0.50\cdot x_1^2\left(\text{level 2}\right) + 0.71\cdot x_1^2\left(\text{level 3}\right)\end{align}\]
Again, the estimated models are shown below.
Marginal Effects for a Model with Curvi-Linear Interactions
\[\begin{align} \mathbb{E}\left[y\right] = -53.77 +~ &28.28 x_1 - 1.27x_1^2 + 65.42\cdot\left(\text{level 2}\right) + 100.22\cdot\left(\text{level 3}\right) +\\ &-11.19\cdot x_1\left(\text{level 2}\right) - 17.22\cdot x_1\left(\text{level 3}\right) +\\ &0.50\cdot x_1^2\left(\text{level 2}\right) + 0.71\cdot x_1^2\left(\text{level 3}\right)\end{align}\]
Again, the estimated models are shown below.
Unsurprisingly, we’ll use {marginaleffects} to check in on the marginal effect of \(x_1\) on \(y\).
Marginal Effects for a Model with Curvi-Linear Interactions
\[\begin{align} \mathbb{E}\left[y\right] = -53.77 +~ &28.28 x_1 - 1.27x_1^2 + 65.42\cdot\left(\text{level 2}\right) + 100.22\cdot\left(\text{level 3}\right) +\\ &-11.19\cdot x_1\left(\text{level 2}\right) - 17.22\cdot x_1\left(\text{level 3}\right) +\\ &0.50\cdot x_1^2\left(\text{level 2}\right) + 0.71\cdot x_1^2\left(\text{level 3}\right)\end{align}\]
Again, the estimated models are shown below.
Unsurprisingly, we’ll use {marginaleffects} to check in on the marginal effect of \(x_1\) on \(y\).
Code
mfx <- slopes(lr_fit,
newdata = my_data,
variable = "x1") %>%
tibble() %>%
mutate(x1 = my_data$x1,
x2 = my_data$x2)
mfx %>%
ggplot() +
geom_ribbon(aes(x = x1,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x1,
y = estimate),
color = "black",
linetype = "dashed") +
labs(x = "x1",
y = "Marginal Effect of x1 on y") +
facet_wrap(~x2) +
theme_bw(base_size = 28)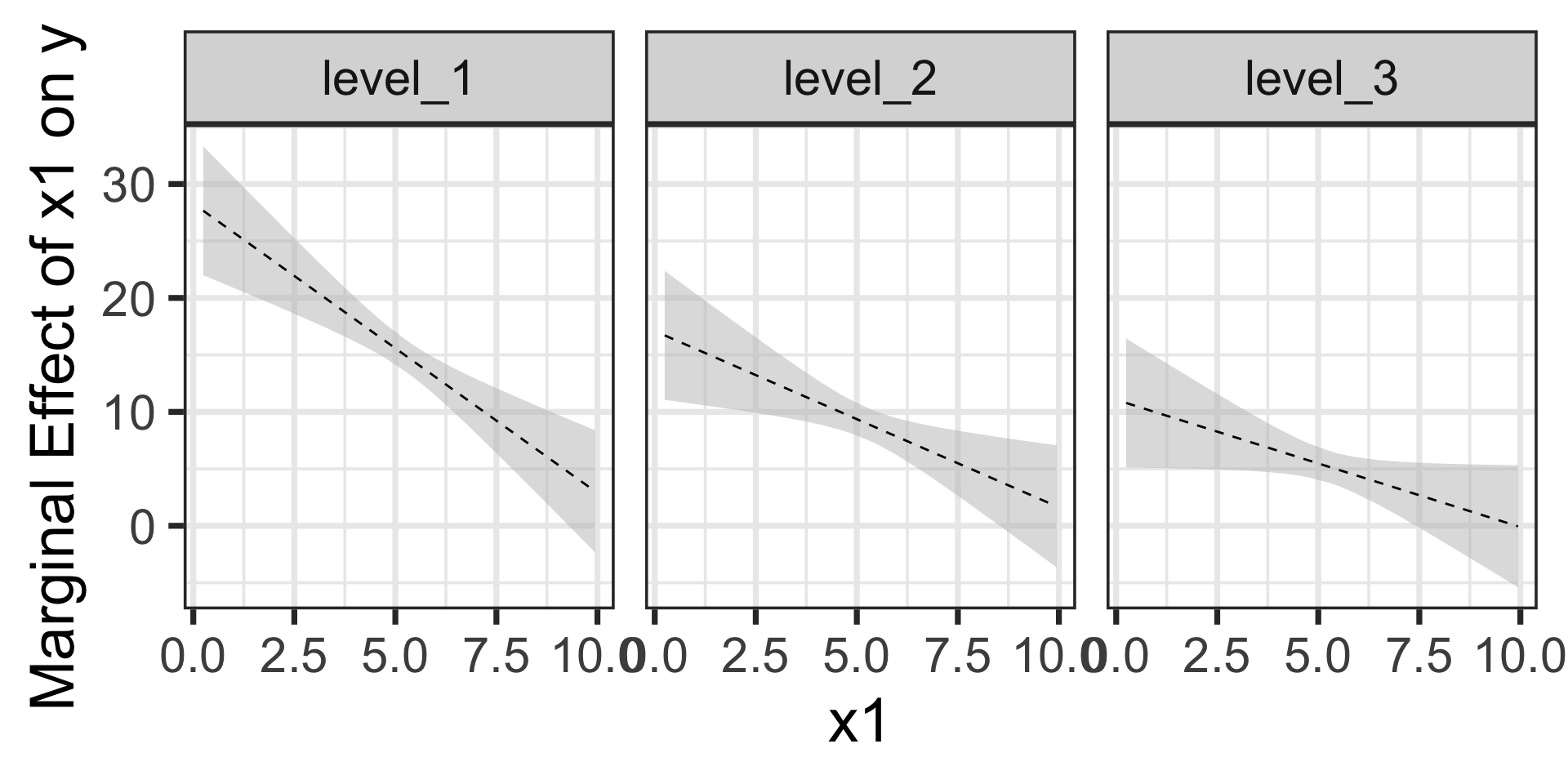
Marginal Effects for a Model with Curvi-Linear Interactions
\[\begin{align} \mathbb{E}\left[y\right] = -53.77 +~ &28.28 x_1 - 1.27x_1^2 + 65.42\cdot\left(\text{level 2}\right) + 100.22\cdot\left(\text{level 3}\right) +\\ &-11.19\cdot x_1\left(\text{level 2}\right) - 17.22\cdot x_1\left(\text{level 3}\right) +\\ &0.50\cdot x_1^2\left(\text{level 2}\right) + 0.71\cdot x_1^2\left(\text{level 3}\right)\end{align}\]
Again, the estimated models are shown below.
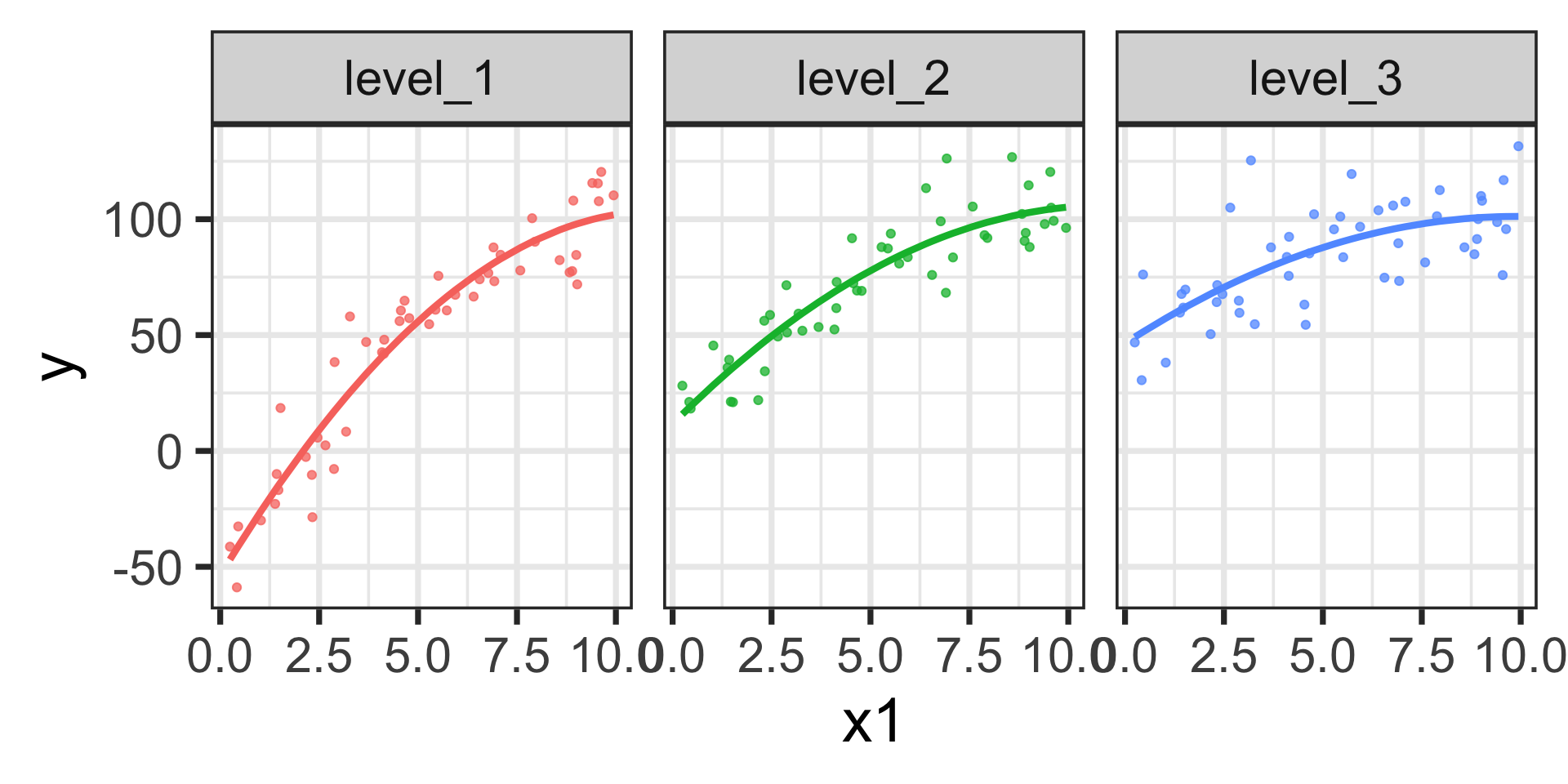
We can see the differences in slopes (marginal effects) and the differences in change in slopes across the three levels of \(x_2\) here. We could still evaluate the marginal effects using calculus if we wanted to.
Unsurprisingly, we’ll use {marginaleffects} to check in on the marginal effect of \(x_1\) on \(y\).
Code
mfx <- slopes(lr_fit,
newdata = my_data,
variable = "x1") %>%
tibble() %>%
mutate(x1 = my_data$x1,
x2 = my_data$x2)
mfx %>%
ggplot() +
geom_ribbon(aes(x = x1,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x1,
y = estimate),
color = "black",
linetype = "dashed") +
labs(x = "x1",
y = "Marginal Effect of x1 on y") +
facet_wrap(~x2) +
theme_bw(base_size = 28)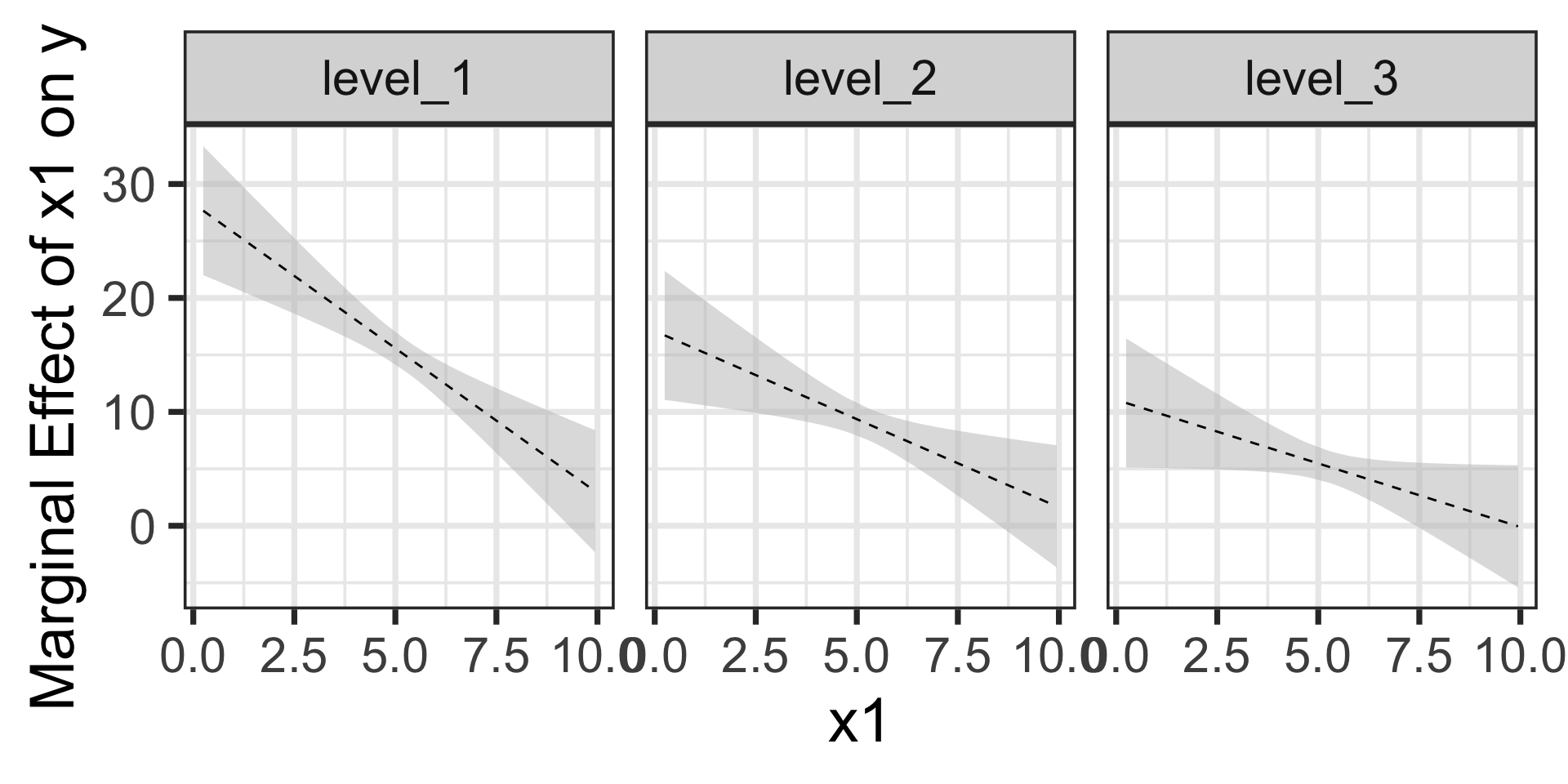
Marginal Effects for a Model with Curvi-Linear Interactions
\[\begin{align} \mathbb{E}\left[y\right] = -53.77 +~ &28.28 x_1 - 1.27x_1^2 + 65.42\cdot\left(\text{level 2}\right) + 100.22\cdot\left(\text{level 3}\right) +\\ &-11.19\cdot x_1\left(\text{level 2}\right) - 17.22\cdot x_1\left(\text{level 3}\right) +\\ &0.50\cdot x_1^2\left(\text{level 2}\right) + 0.71\cdot x_1^2\left(\text{level 3}\right)\end{align}\]
Again, the estimated models are shown below.
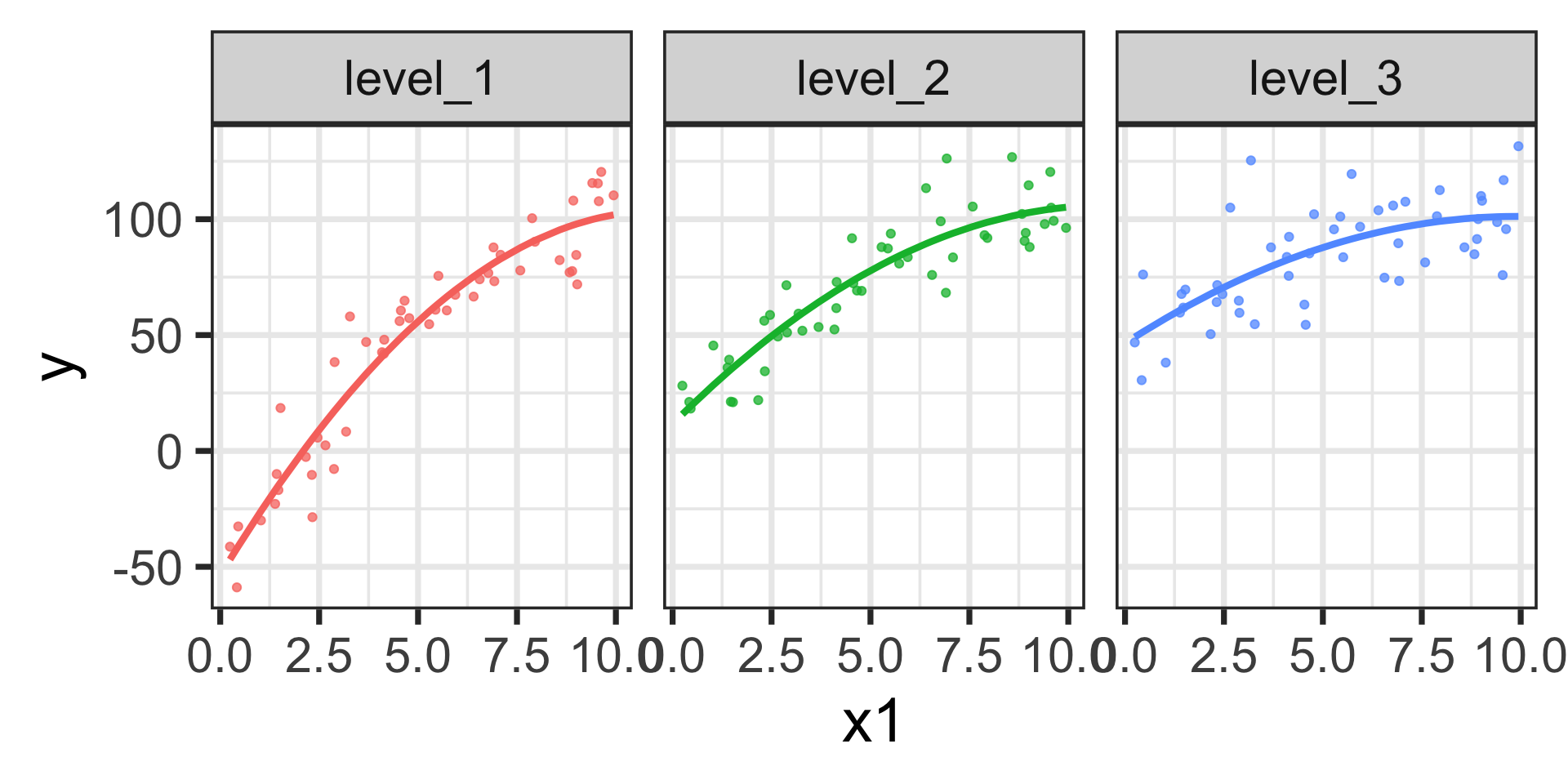
We can see the differences in slopes (marginal effects) and the differences in change in slopes across the three levels of \(x_2\) here. We could still evaluate the marginal effects using calculus if we wanted to.
Unsurprisingly, we’ll use {marginaleffects} to check in on the marginal effect of \(x_1\) on \(y\).
Code
mfx <- slopes(lr_fit,
newdata = my_data,
variable = "x1") %>%
tibble() %>%
mutate(x1 = my_data$x1,
x2 = my_data$x2)
mfx %>%
ggplot() +
geom_ribbon(aes(x = x1,
ymin = conf.low,
ymax = conf.high),
fill = "grey",
alpha = 0.5) +
geom_line(aes(x = x1,
y = estimate),
color = "black",
linetype = "dashed") +
labs(x = "x1",
y = "Marginal Effect of x1 on y") +
facet_wrap(~x2) +
theme_bw(base_size = 28)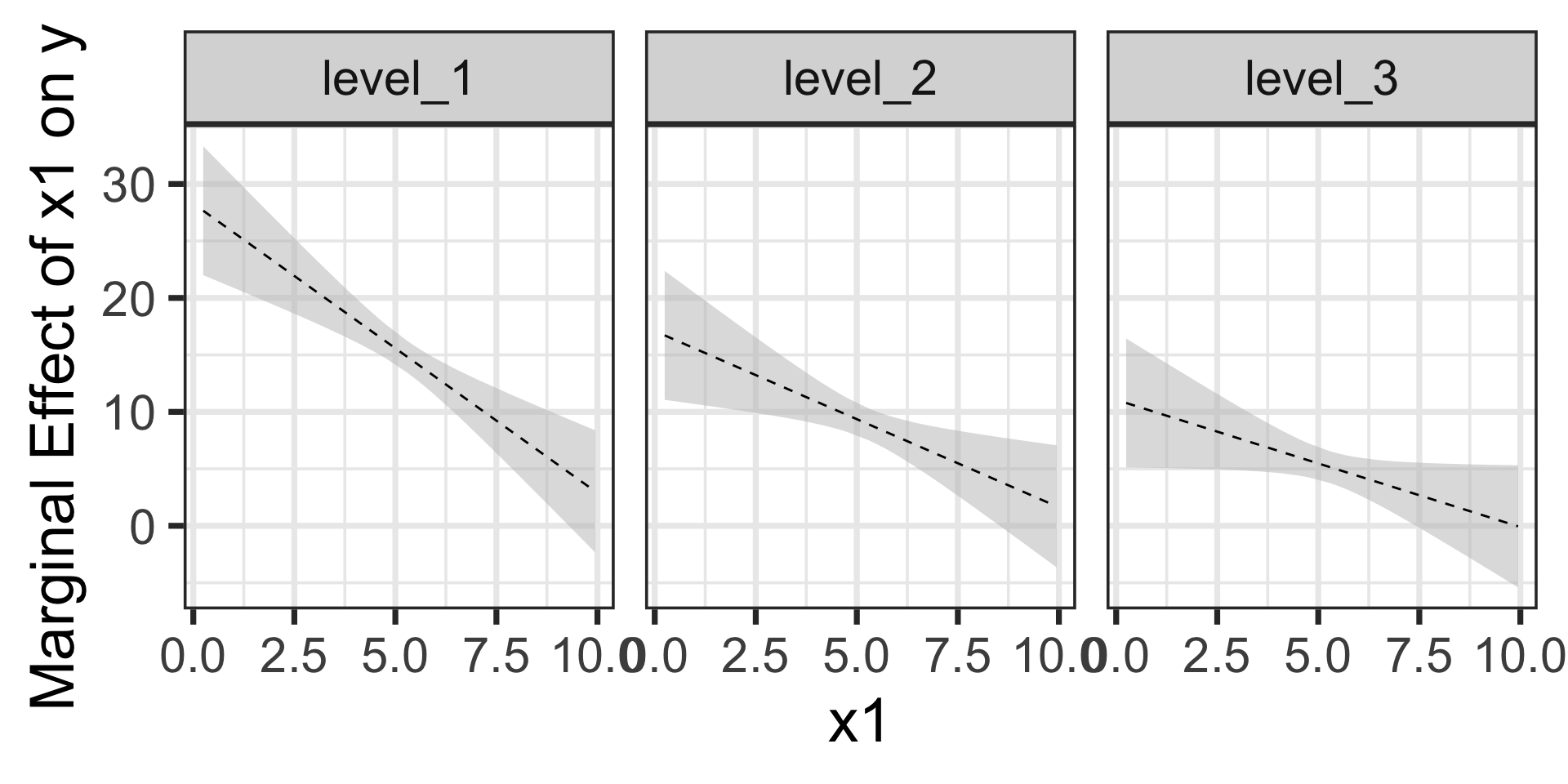
What was challenging to investigate without calculus is made easier with {marginaleffects}
Summary
Interpreting the effect of a unit change in a predictor on the response is called interpreting that predictor’s marginal effect
Interpreting a predictor’s marginal effect requires computing the partial derivative of our model with respect to that predictor – a topic from calculus
The
{marginaleffects}package can help us obtain and interpret marginal effects without having to know or use calculusIn order to obtain marginal effects for a fitted model we…
- Begin with the fitted model object
- Extract the fit using
extract_fit_engine() - Pass the result to the
slopes()function from{marginaleffects} - Provide our training data as the
newdataargument and identify the variable we are calculating marginal effects for - Plot the results (optional)
Note: Currently, the
slopes()function doesn’t pass the values of the predictors to its resulting data frame correctly – I’ve filed an issue on this with the developer and we are working on a fix for it – for now, you can justmutate()over the incorrect predictor values with the values from the training data frame
Next Time…
In-Class Halloween Modeling Competition