MAT 370: Cubic Spline Interpolants

Dr. Gilbert

December 29, 2025

Motivation and Context

At the end of our last discussion, we saw that increasing the number of observed data points also increases the degree of the polynomial.

High degree polynomials invite greater levels of variability between control points, especially near the boundaries of the observed region.

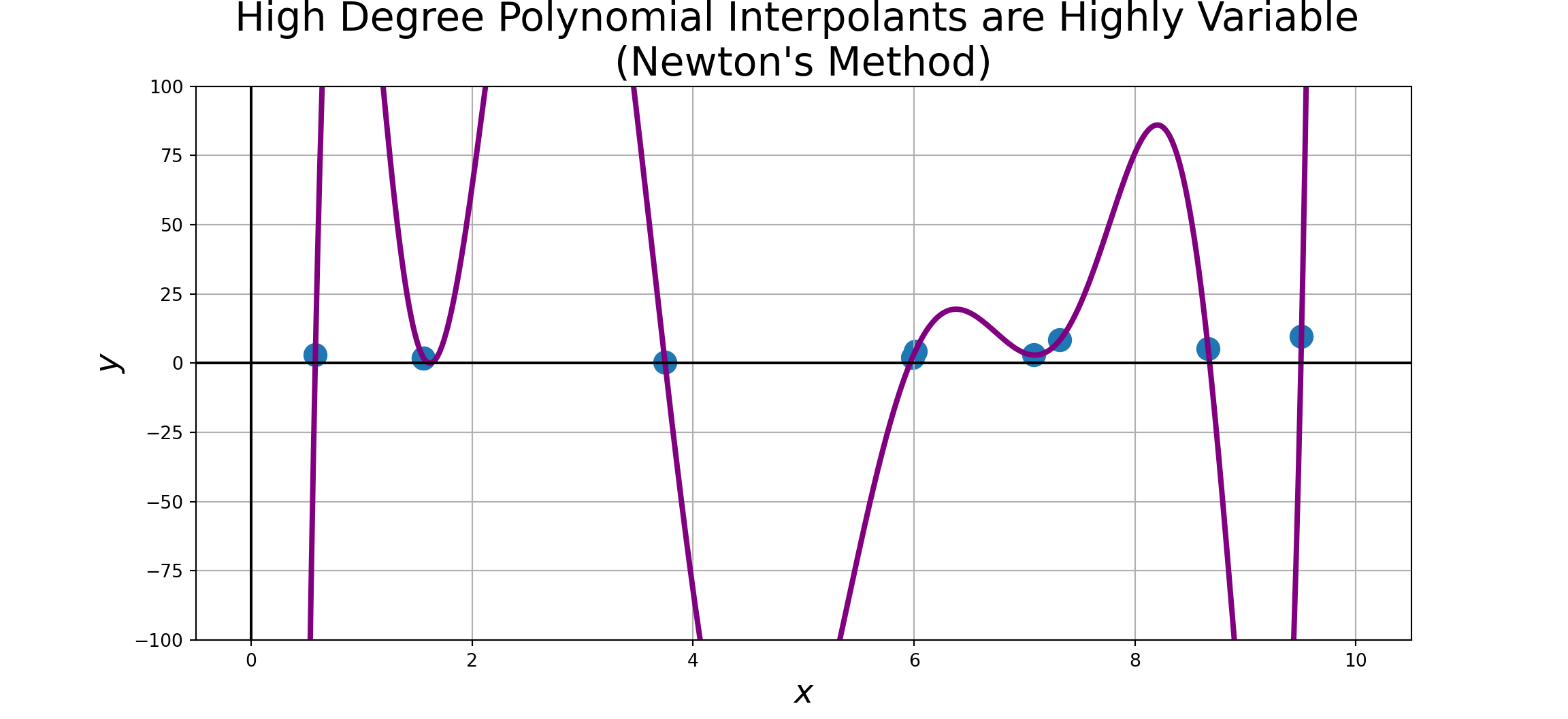
Alternative Interpolation Strategies

There are other classes of interpolant which reduce this unjustified oscillation.

• Piecewise-linear interpolants
• Nearest neighbor interpolants
• Inverse distance weighting interpolants
• Splines
• etc.

In this discussion, we’ll focus on natural cubic splines.

▶ Video from Steve Seitz at Graphics in Five Minutes.

Natural Cubic Splines and Unloaded Beams

We’ve seen that polynomial interpolation should be done with as few data points as is feasible.

This is counterintuitive because we usually think of more information as better.

If we have more than just a few data points, then a cubic spline is a great option to use as an interpolant.

Cubic splines consist of

• pins (or knots)
• elastic stips

The pins are the observed data points, and the elastic strips correspond to “unloaded beams” connecting the pins.

There is some nice connection to engineering here because the deflection (\(\omega\)) of an unloaded beam with two connection points with constant flexural rigidity satisfies \(\frac{d^4\omega}{dx^4} = \frac{q\left(x\right)}{EI}\), where \(q\left(x\right)\) is the load at position \(x\) along the beam.

Since our elastic strips correspond to unweighted beams, these strips satisfy \(\frac{d^4\omega}{dx^4} = 0\).

Constraints: Natural Cubic Splines

Since our elastic strips satisfy \(\frac{d^4\omega}{dx^4} = 0\), we know that the strips are cubic polynomials.

We impose a few additional constraints on our cubic splines as well.

1. The slope (first derivative) is continuous through each pin.
2. The curvature (second derivative) is continuous through each pin.
3. The curvature at the left-most and right-most pins is \(0\).

Because of these constraints, our cubic splines will have more moe controlled behavior.

Constructing Cubic Splines

We’ll actually go through the math here because its a really nice application of your first two semesters of calculus.

Before we dive in, a few comments to keep us grounded.

Strategy: The strategy we’re going to use pulls from Calculus I, Calculus II, and Linear Algebra.

1. Since we know \(f_{i, i + 1}^{\left(4\right)}\left(x\right) = 0\) (since \(\frac{d^4\omega}{dx^4} = 0\)), we know \(f_{i, i+1}^{\left(3\right)}\left(x\right)\) is constant, and \(f_{i, i+1}^{''}\left(x\right)\) is linear.
2. Construct a linear interpolant for the second derivative.
3. Integrate it once to obtain the slopes.
4. Integrate again to obtain the cubic sections.
5. Use the constraints to determine the constants.

Setting Expectations: You will not be expected to memorize or reproduce this argument. You should be able to follow it, discuss the main strategy, and identify where ideas we’ve encountered in MAT370 are being leveraged.

Constructing Cubic Splines

Consider a set of \(n+1\) observed data points \(\left(x_0, y_0\right),~\left(x_1, y_1\right),~\cdots,~\left(x_n, y_n\right)\) with \(x_0 < x_1 < \cdots < x_n\).

A cubic spline interpolant will consist of \(n\) cubic segments, \(f_{i, i+1}\left(x\right)\) for \(i = 0,~1,~\cdots,~n-1\).

The full cubic spline interpolant is a piecewise cubic consisting of each of these cubic sections, having continuous first- and second-derivatives at each of the pins (observed data points).

Because we know that each segment is a cubic, and that the second derivative of the spline interpolant is continuous, we must have that the second derivative to the left and right of each pin point match.

That is, for any \(i\)

\[f_{i-1,i}''\left(x_i\right) = f_{i, i+1}''\left(x_i\right) = k_i\]

We know that \(k_0 = k_n = 0\), but all of the other \(k_i\) are unknown and need to be solved for.

We can use Lagrange’s two-point interpolation as a starting point for computing the unknown coefficients of each \(f_{i,i+1}\left(x\right)\).

We can write

\[f_{i,i+1}''\left(x\right) = k_i\ell_i\left(x\right) + k_{i+1}\ell_{i+1}\left(x\right)\]

where \(\ell_{i}\left(x\right) = \frac{x - x_{i+1}}{x_i - x_{i+1}}\) and \(\ell_{i+1}\left(x\right) = \frac{x - x_i}{x_{i+1} - x_i}\)

Constructing Cubic Splines (Cont’d)

We start from where we just left off.

\[\begin{align*} f_{i,i+1}''\left(x\right) &= k_i\left(\frac{x - x_{i+1}}{x_i - x_{i+1}}\right) + k_{i+1}\left(\frac{x - x_i}{x_{i+1} - x_i}\right) \end{align*}\]

Constructing Cubic Splines (Cont’d)

We start from where we just left off.

\[\begin{align*} f_{i,i+1}''\left(x\right) &= k_i\left(\frac{x - x_{i+1}}{x_i - x_{i+1}}\right) + k_{i+1}\left(\frac{x - x_i}{x_{i+1} - x_i}\right)\\ \implies f_{i,i+1}''\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}} \end{align*}\]

Constructing Cubic Splines (Cont’d)

We start from where we just left off.

\[\begin{align*} f_{i,i+1}''\left(x\right) &= k_i\left(\frac{x - x_{i+1}}{x_i - x_{i+1}}\right) + k_{i+1}\left(\frac{x - x_i}{x_{i+1} - x_i}\right)\\ \implies f_{i,i+1}''\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}\\ \implies \int{f_{i,i+1}''\left(x\right)dx} &= \int{\frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}dx} \end{align*}\]

Constructing Cubic Splines (Cont’d)

We start from where we just left off.

\[\begin{align*} f_{i,i+1}''\left(x\right) &= k_i\left(\frac{x - x_{i+1}}{x_i - x_{i+1}}\right) + k_{i+1}\left(\frac{x - x_i}{x_{i+1} - x_i}\right)\\ \implies f_{i,i+1}''\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}\\ \implies \int{f_{i,i+1}''\left(x\right)dx} &= \int{\frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}dx}\\ \implies f_{i,i+1}'\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right)^2 - k_{i+1}\left(x - x_i\right)^2}{2\left(x_i - x_{i+1}\right)} + C_1 \end{align*}\]

Constructing Cubic Splines (Cont’d)

We start from where we just left off.

\[\begin{align*} f_{i,i+1}''\left(x\right) &= k_i\left(\frac{x - x_{i+1}}{x_i - x_{i+1}}\right) + k_{i+1}\left(\frac{x - x_i}{x_{i+1} - x_i}\right)\\ \implies f_{i,i+1}''\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}\\ \implies \int{f_{i,i+1}''\left(x\right)dx} &= \int{\frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}dx}\\ \implies f_{i,i+1}'\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right)^2 - k_{i+1}\left(x - x_i\right)^2}{2\left(x_i - x_{i+1}\right)} + C_1\\ \implies \int{f_{i,i+1}'\left(x\right)dx} &= \int{\frac{k_i\left(x - x_{i+1}\right)^2 - k_{i+1}\left(x - x_i\right)^2}{2\left(x_i - x_{i+1}\right)} + C_1dx} \end{align*}\]

Constructing Cubic Splines (Cont’d)

We start from where we just left off.

\[\begin{align*} f_{i,i+1}''\left(x\right) &= k_i\left(\frac{x - x_{i+1}}{x_i - x_{i+1}}\right) + k_{i+1}\left(\frac{x - x_i}{x_{i+1} - x_i}\right)\\ \implies f_{i,i+1}''\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}\\ \implies \int{f_{i,i+1}''\left(x\right)dx} &= \int{\frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}dx}\\ \implies f_{i,i+1}'\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right)^2 - k_{i+1}\left(x - x_i\right)^2}{2\left(x_i - x_{i+1}\right)} + C_1\\ \implies \int{f_{i,i+1}'\left(x\right)dx} &= \int{\frac{k_i\left(x - x_{i+1}\right)^2 - k_{i+1}\left(x - x_i\right)^2}{2\left(x_i - x_{i+1}\right)} + C_1dx}\\ \implies f_{i,i+1}\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right)^3 - k_{i+1}\left(x - x_i\right)^3}{3\cdot 2\left(x_i - x_{i+1}\right)} + C_1x + C_2\\ \end{align*}\]

Constructing Cubic Splines (Cont’d)

We start from where we just left off.

\[\begin{align*} f_{i,i+1}''\left(x\right) &= k_i\left(\frac{x - x_{i+1}}{x_i - x_{i+1}}\right) + k_{i+1}\left(\frac{x - x_i}{x_{i+1} - x_i}\right)\\ \implies f_{i,i+1}''\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}\\ \implies \int{f_{i,i+1}''\left(x\right)dx} &= \int{\frac{k_i\left(x - x_{i+1}\right) - k_{i+1}\left(x - x_i\right)}{x_i - x_{i+1}}dx}\\ \implies f_{i,i+1}'\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right)^2 - k_{i+1}\left(x - x_i\right)^2}{2\left(x_i - x_{i+1}\right)} + C_1\\ \implies \int{f_{i,i+1}'\left(x\right)dx} &= \int{\frac{k_i\left(x - x_{i+1}\right)^2 - k_{i+1}\left(x - x_i\right)^2}{2\left(x_i - x_{i+1}\right)} + C_1dx}\\ \implies f_{i,i+1}\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right)^3 - k_{i+1}\left(x - x_i\right)^3}{3\cdot 2\left(x_i - x_{i+1}\right)} + C_1x + C_2\\ \end{align*}\]

If we let \(C_1 = A - B\) and \(C_2 = -Ax_{i+1} + Bx_i\), then we can write the final line to the left as

\[f_{i,i+1}\left(x\right) = \frac{k_i\left(x - x_{i+1}\right)^3 - k_{i+1}\left(x - x_i\right)^3}{3\cdot 2\left(x_i - x_{i+1}\right)} + A\left(x - x_{i+1}\right) - B\left(x - x_i\right)\]

This will be more convenient algorithmically.

Remembering that \(f_{i, i+1}\left(x_i\right) = y_i\), then we obtain

\[\frac{k_i\left(x_i - x_{i+1}\right)^3}{6\left(x_i - x_{i+1}\right)} + A\left(x_i - x_{i+1}\right) = y_i\]

So we have

\[\boxed{A = \frac{y_i}{x_i - x_{i+1}} - \frac{k_i\left(x_i - x_{i+1}\right)}{6}}\]

Evaluating \(f_{i,i+1}\left(x_{i+1}\right)\) similarly gives us

\[\boxed{B = \frac{y_{i+1}}{x_i - x_{i+1}} - \frac{k_{i+1}\left(x_i - x_{i+1}\right)}{6}}\]

Constructing Cubic Splines (Cont’d)

At this stage, we know that

\[\boxed{A = \frac{y_i}{x_i - x_{i+1}} - \frac{k_i\left(x_i - x_{i+1}\right)}{6}}~~~~\text{and}~~~~\boxed{B = \frac{y_{i+1}}{x_i - x_{i+1}} - \frac{k_{i+1}\left(x_i - x_{i+1}\right)}{6}}\]

Substituting these values back, we have discovered \(f_{i,i+1}\left(x\right)\). That is,

\[\begin{align*} f_{i,i+1}\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right)^3 - k_{i+1}\left(x - x_i\right)^3}{6\left(x_i - x_{i+1}\right)} + \left(\frac{y_i}{x_i - x_{i+1}} - \frac{k_i\left(x_i - x_{i+1}\right)}{6}\right)\left(x - x_{i+1}\right) - \left(\frac{y_{i+1}}{x_i - x_{i+1}} - \frac{k_{i+1}\left(x_i - x_{i+1}\right)}{6}\right)\left(x - x_{i+1}\right) \end{align*}\]

Constructing Cubic Splines (Cont’d)

At this stage, we know that

\[\boxed{A = \frac{y_i}{x_i - x_{i+1}} - \frac{k_i\left(x_i - x_{i+1}\right)}{6}}~~~~\text{and}~~~~\boxed{B = \frac{y_{i+1}}{x_i - x_{i+1}} - \frac{k_{i+1}\left(x_i - x_{i+1}\right)}{6}}\]

Substituting these values back, we have discovered \(f_{i,i+1}\left(x\right)\). That is,

\[\begin{align*} f_{i,i+1}\left(x\right) &= \frac{k_i\left(x - x_{i+1}\right)^3 - k_{i+1}\left(x - x_i\right)^3}{6\left(x_i - x_{i+1}\right)} + \left(\frac{y_i}{x_i - x_{i+1}} - \frac{k_i\left(x_i - x_{i+1}\right)}{6}\right)\left(x - x_{i+1}\right) - \left(\frac{y_{i+1}}{x_i - x_{i+1}} - \frac{k_{i+1}\left(x_i - x_{i+1}\right)}{6}\right)\left(x - x_{i+1}\right)\\[12pt] &= \frac{k_i}{6}\left(\frac{\left(x - x_{i+1}\right)^3}{x_{i} - x_{i+1}} - \left(x_i - x_{i+1}\right)\left(x - x_{i+1}\right)\right) - \frac{k_{i+1}}{6}\left(\frac{\left(x - x_i\right)^3}{x_i - x_{i+1}} - \left(x-x_i\right)\left(x_i - x_{i+1}\right)\right) + \frac{y_i\left(x - x_{i+1}\right) - y_{i+1}\left(x - x_i\right)}{x_i -x_{i+1}} \end{align*}\]

Constructing Cubic Splines (Cont’d)

We can now use the continuity of the derivative at each of the knot values to determine the remaining \(k_i\) values.

We know that \(f_{i-1, i}'\left(x_i\right) = f_{i, i+1}'\left(x_i\right)\) for \(i \in [n-1]\).

Some algebra brings us to the following linear system:

\[\left\{\begin{array}{lcl} k_{i-1}\left(x_{i-1} - x_i\right) + 2k_i\left(x_{i-1} - x_{i+1}\right) + k_{i+1}\left(x_i - x_{i+1}\right) & = & 6\left(\frac{y_{i-1} - y_i}{x_{i-1} - x_i} - \frac{y_i - y_{i+1}}{x_i - x_{i+1}}\right)\end{array}\right.~~~~\text{for } i\in [n - 1]\]

Notice that the corresponding coefficient matrix will be a tridiagonal – indeed, each equation in the system uses index \(i-1\), \(i\), and \(i+1\) only.

This means that we can solve the system using our DoolittleLUdecomp3() routine from our Day 6 discussion.

Implementing the Cubic Spline Interpolant

We are finally ready to define the components for our cubic spline interpolator routine.

As a reminder, since we need a routine from an earlier notebook, we’ll need to copy/paste that routine into any notebook where we want to use this one. In the interest of space, I’m not showing that pasting here.

def curvatures(xData, yData):
  n = len(xData) - 1
  c = np.zeros(n)
  d = np.ones(n+1)
  e = np.zeros(n)
  k = np.zeros(n+1)

  c[0:(n-1)] = xData[0:(n-1)] - xData[1:n]
  d[1:n] = 2.0*(xData[0:(n-1)] - xData[2:(n+1)])
  e[1:n] = xData[1:n] - xData[2:(n+1)]
  k[1:n] = 6.0*((yData[0:(n-1)] - yData[1:n])/(xData[0:(n-1)] - xData[1:n])) - 6.0*((yData[1:n] - yData[2:(n+1)])/(xData[1:n] - xData[2:(n+1)]))

  DoolittleLUdecomp3solver(c, d, e, k)

  return k

def findSegment(xData, x):
    iLeft = 0
    iRight = len(xData) - 1

    while 1:
      if (iRight - iLeft) <= 1:
        return iLeft
      i = int((iLeft + iRight)/2)
      if x < xData[i]:
        iRight = i
      else:
        iLeft = i

def evalSpline(xData, yData, k, x):
  i = findSegment(xData, x)
  h = xData[i] - xData[i+1]
  #y = ((x - xData[i+1])**3/h - (x - xData[i+1])*h)*k[i]/6.0 - ((x - xData[i])**3/h - (x - xData[i])*h)*k[i+1]/6.0 + (yData[i]*(x - xData[i+1]) - yData[i+1]*(x - xData[i]))/h
  y = ((x - xData[i+1])**3/h - (x - xData[i+1])*h)*k[i]/6.0 - ((x - xData[i])**3/h - (x - xData[i])*h)*k[i+1]/6.0 + (yData[i]*(x - xData[i+1]) - yData[i+1]*(x - xData[i]))/h


  return y

Comments on the Interpolant

This is the first time we have a routine which is split across multiple functions without a complete wrapper for the entire process (though you could build one).

• The curvatures() function solves the tridiagonal system which we discovered through the math on the previous slides.

• The findSegment() function is a helper function for evaluating the cubic spline interpolant.

  • You won’t use this function directly.

• The evalSpline() function is the one you’ll use to take new input values and to evaluate the cubic spline interpolants and obtain outputs.

Using the Interpolant

Example: Use the cubic spline interpolator we just constructed to build a cubic spline interpolant for the observed data to the right.

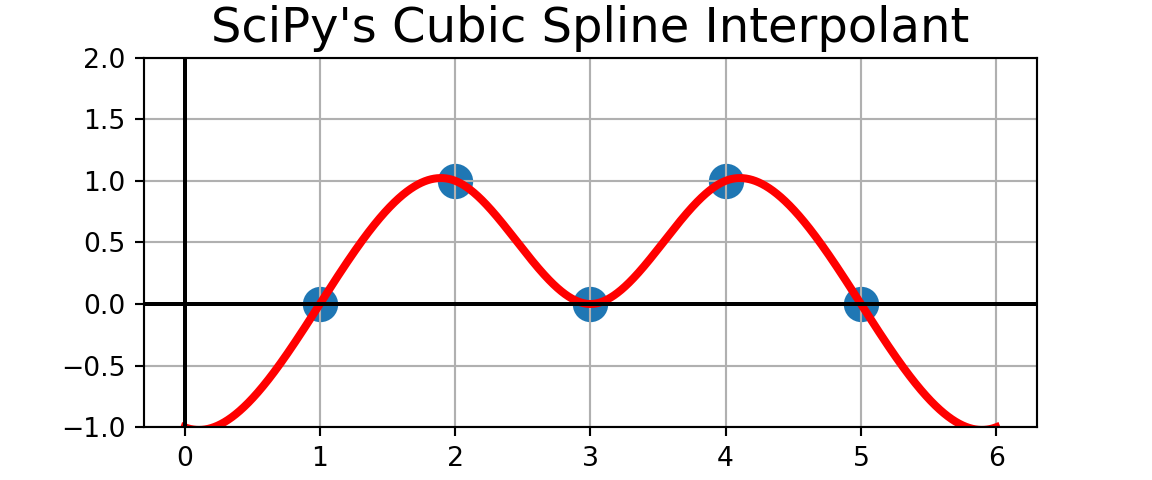
If you like, compare your cubic spline interpolant to the one produced by CubicSpline() from scipy.interpolate. Before executing the code to compare, what do you expect to see?

x	y
1	0
2	1
3	0
4	1
5	0

x = np.array([1.0, 2, 3, 4, 5])
y = np.array([0.0, 1, 0, 1, 0])

x_new = np.linspace(0, 6, 10000)

k = curvatures(x, y)

y_new = x_new.copy()
for j in range(len(x_new)):
  y_new[j] = evalSpline(x, y, k, x_new[j])

plt.figure(figsize = (6,2))
plt.scatter(x, y, s = 150)
plt.plot(x_new, y_new, color = "purple", linewidth = 3)
plt.grid()
plt.axvline(color = "black")
plt.axhline(color = "black")
plt.title("Our Cubic Spline Interpolant", fontsize = 18)
plt.ylim((-1, 2));
plt.show()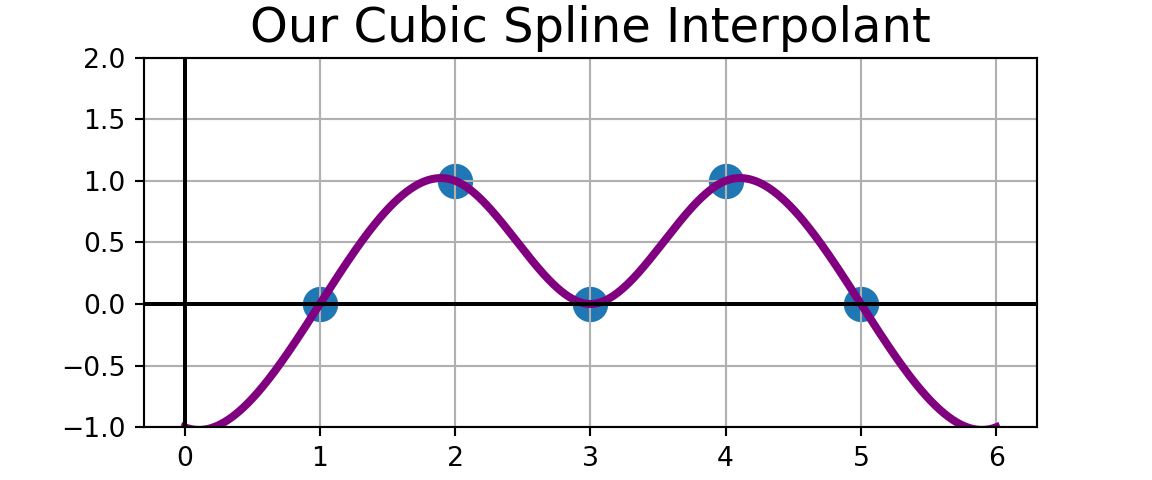

Using the Interpolant

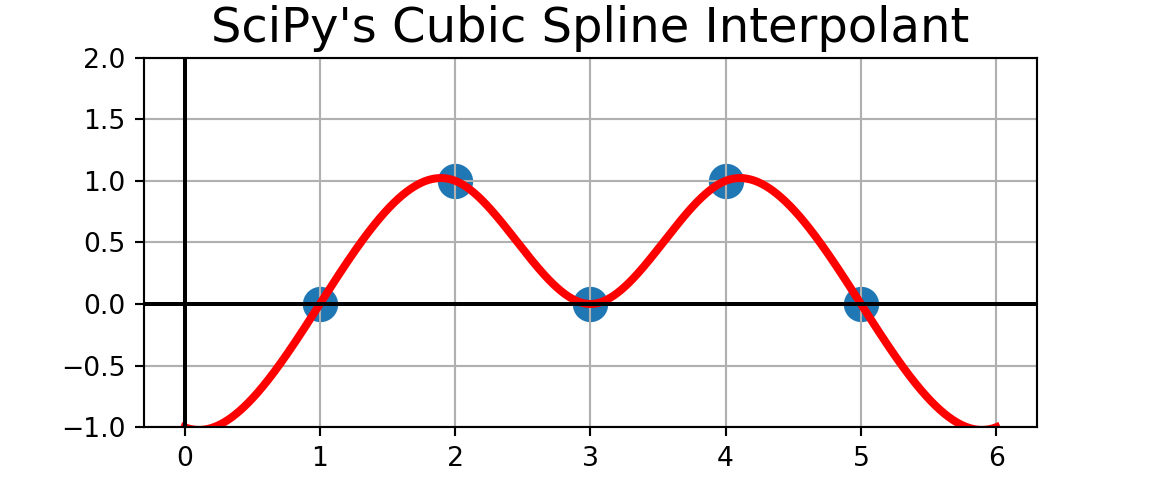
Example: Use the cubic spline interpolator we just constructed to build a cubic spline interpolant for the observed data to the right.

If you like, compare your cubic spline interpolant to the one produced by CubicSpline() from scipy.interpolate. Before executing the code to compare, what do you expect to see? They’re the same!

x	y
1	0
2	1
3	0
4	1
5	0

x = np.array([1.0, 2, 3, 4, 5])
y = np.array([0.0, 1, 0, 1, 0])

x_new = np.linspace(0, 6, 10000)

k = curvatures(x, y)

y_new = x_new.copy()
for j in range(len(x_new)):
  y_new[j] = evalSpline(x, y, k, x_new[j])

plt.figure(figsize = (6,2))
plt.scatter(x, y, s = 150)
plt.plot(x_new, y_new, color = "purple", linewidth = 3)
plt.grid()
plt.axvline(color = "black")
plt.axhline(color = "black")
plt.title("Our Cubic Spline Interpolant", fontsize = 18)
plt.ylim((-1, 2));
plt.show()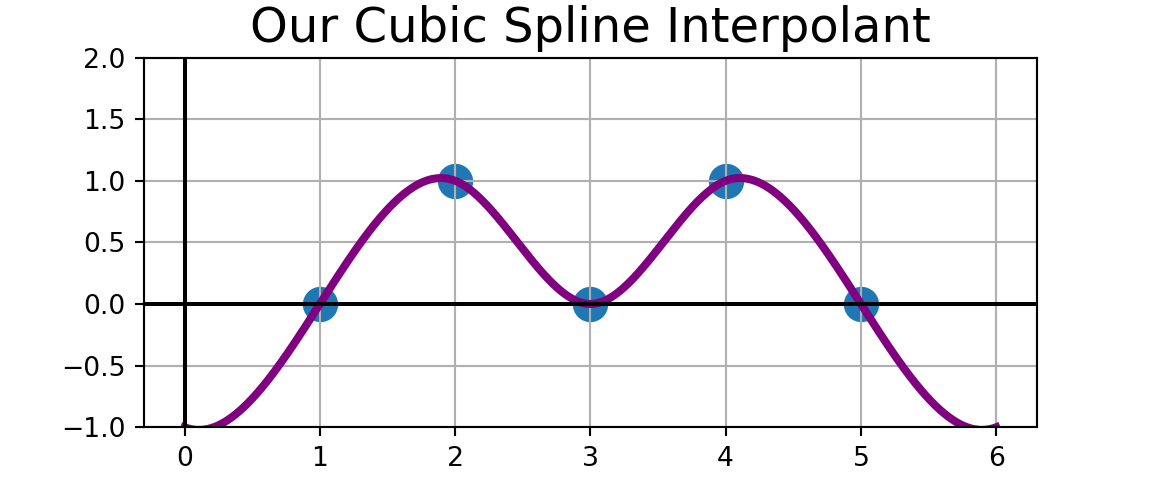

Summary

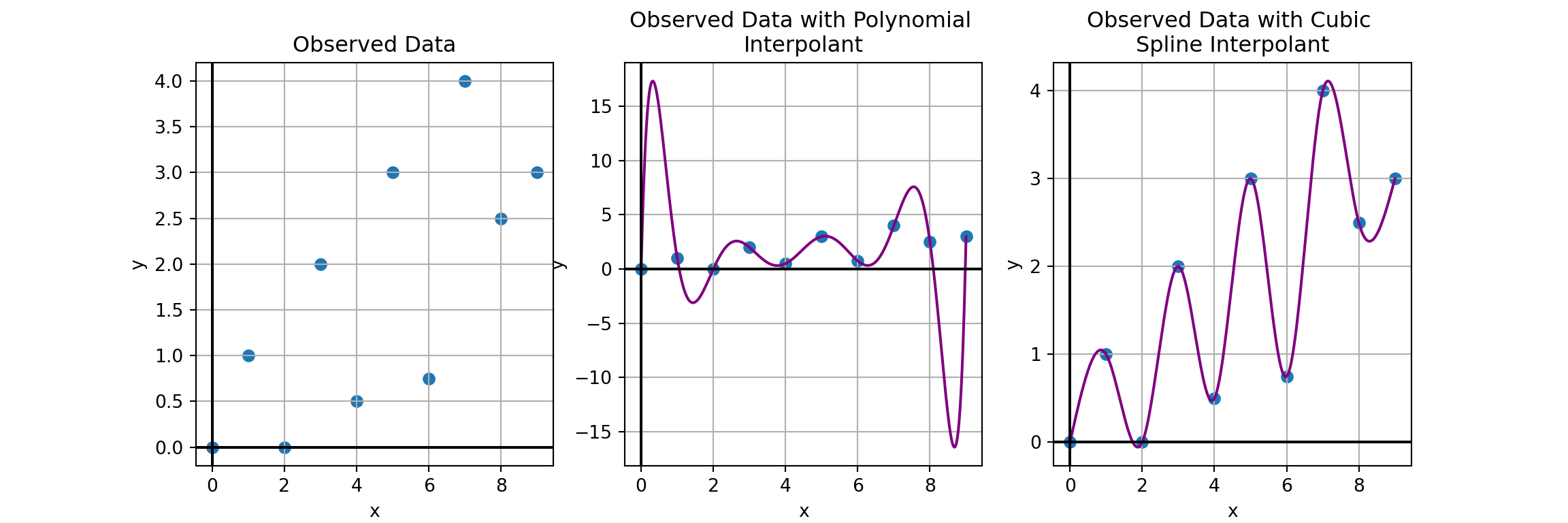
• In this discussion we introduced cubic spline interpolants as possibly better global interpolants than polynomial interpolants.

• What is meant by “better global interpolant” can be seen from our original set of toy observations with the polynomial and cubic spline interpolant near the beginning of this slide deck.

  • The polynomial interpolant seems to fit the interior observations and the intervals between them in a reasonable manner.

  • The performance of the polynomial interpolant along the left-most and right-most intervals should seem suspect, though.

  • The interpolant’s range along those intervals is very wide and potentially unsupportedly so.

  • The cubic spline interpolant, however, doesn’t exhibit this behavior.

• For this reason, cubic spline interpolants are often preferred over polynomial interpolants.

Next Time

We switch gears and look at linear regression via ordinary least squares for curve fitting rather than full interpolation.