MAT 350: Vectors, Vector Arithmetic, and Operations
September 8, 2025
Vectors (Definition)
- A vector is a quantity with both magnitude and direction.
- Vectors are often represented as arrays of numbers:
\[\vec{v} = \left[\begin{array}{r} v_1 \\ v_2 \\ \vdots \\ v_n \end{array}\right] \text{(column vector)} \qquad \vec{u} = \left[\begin{array}{r} u_1 & u_2 & \cdots & u_n \end{array}\right] \quad \text{(row vector)}\]
Example: Consider the vectors \(\vec{v} = \begin{bmatrix} 1\\ -8\\ 3/2\end{bmatrix}\) and \(\vec{u} = \begin{bmatrix} -11 & 17 & 0 & \pi\end{bmatrix}\)
Transposing Vectors
We can turn a column vector into a row vector (and vice-versa) by taking its transpose.
We denote the transpose operation via the superscript \(^T\).
Consider the vector \(\vec{v}\) and its transpose below.
\[\vec{v} = \begin{bmatrix} v_1\\ v_2\\ \vdots \\ v_n\end{bmatrix} \qquad \vec{v}^T = \begin{bmatrix} v_1 & v_2 & \cdots & v_n\end{bmatrix}\]
Transposing Vectors (Examples)
Example: For each of the vectors below, construct the transpose.
- Let \(\vec{v} = \begin{bmatrix} 1/2\\ -11\\ 3\\ 0\\ 8\end{bmatrix}\), then \(\vec{v}^T\) is given by…
\[\vec{v}^T = \begin{bmatrix} 1/2 & -11 & 3 & 0 & 8\end{bmatrix}\]
- Let \(\vec{u} = \begin{bmatrix} 8 & -1\end{bmatrix}\), then \(\vec{u}^T\) is the vector…
\[\vec{u}^T = \begin{bmatrix} 8\\ -1\end{bmatrix}\]
Vector Addition and Subtraction
Addition and subtraction of vectors is done component-wise:
\[\vec{u} + \vec{v} = \begin{bmatrix} u_1 + v_1 \\ u_2 + v_2\\ \vdots \\ u_n + v_n \end{bmatrix} \quad \vec{u} - \vec{v} = \begin{bmatrix} u_1 - v_1 \\ u_2 - v_2\\ \vdots\\ u_n - v_n \end{bmatrix}\]
Example: Consider the vectors \(\vec{u}\), \(\vec{v}\), and \(\vec{w}\) below. For those that are compatible, compute the sums and differences of the vectors. For those that are not compatible, describe why.
\[\vec{u} = \begin{bmatrix} -5\\ 0\\ 8\\ 1\end{bmatrix}~~~~~\vec{v} = \begin{bmatrix} 1\\ -1\\ 1\end{bmatrix}~~~~~\vec{w} = \begin{bmatrix} 1\\ 0\\ 0\\ -9\end{bmatrix}\]
Vector Addition And Subtraction
Example: Consider the vectors \(\vec{u}\), \(\vec{v}\), and \(\vec{w}\) below. For those that are compatible, compute the sums and differences of the vectors. For those that are not compatible, describe why.
\[\vec{u} = \begin{bmatrix} -5\\ 0\\ 8\\ 1\end{bmatrix}~~~~~\vec{v} = \begin{bmatrix} 1\\ -1\\ 1\end{bmatrix}~~~~~\vec{w} = \begin{bmatrix} 1\\ 0\\ 0\\ -9\end{bmatrix}\]
- Vector \(\vec{v}\)’s dimension doesn’t match, so it is not compatible with \(\vec{u}\) or \(\vec{w}\)
\[\vec{u} + \vec{w} = \begin{bmatrix} -5\\ 0\\ 8\\ 1\end{bmatrix} + \begin{bmatrix} 1\\ 0\\ 0\\ -9\end{bmatrix} = \begin{bmatrix} -4\\ 0\\ 8\\ -8\end{bmatrix}\]
Vector Addition And Subtraction
Example: Consider the vectors \(\vec{u}\), \(\vec{v}\), and \(\vec{w}\) below. For those that are compatible, compute the sums and differences of the vectors. For those that are not compatible, describe why.
\[\vec{u} = \begin{bmatrix} -5\\ 0\\ 8\\ 1\end{bmatrix}~~~~~\vec{v} = \begin{bmatrix} 1\\ -1\\ 1\end{bmatrix}~~~~~\vec{w} = \begin{bmatrix} 1\\ 0\\ 0\\ -9\end{bmatrix}\]
- Find \(\vec{u} - \vec{w}\)
- Find \(\vec{w} - \vec{u}\)
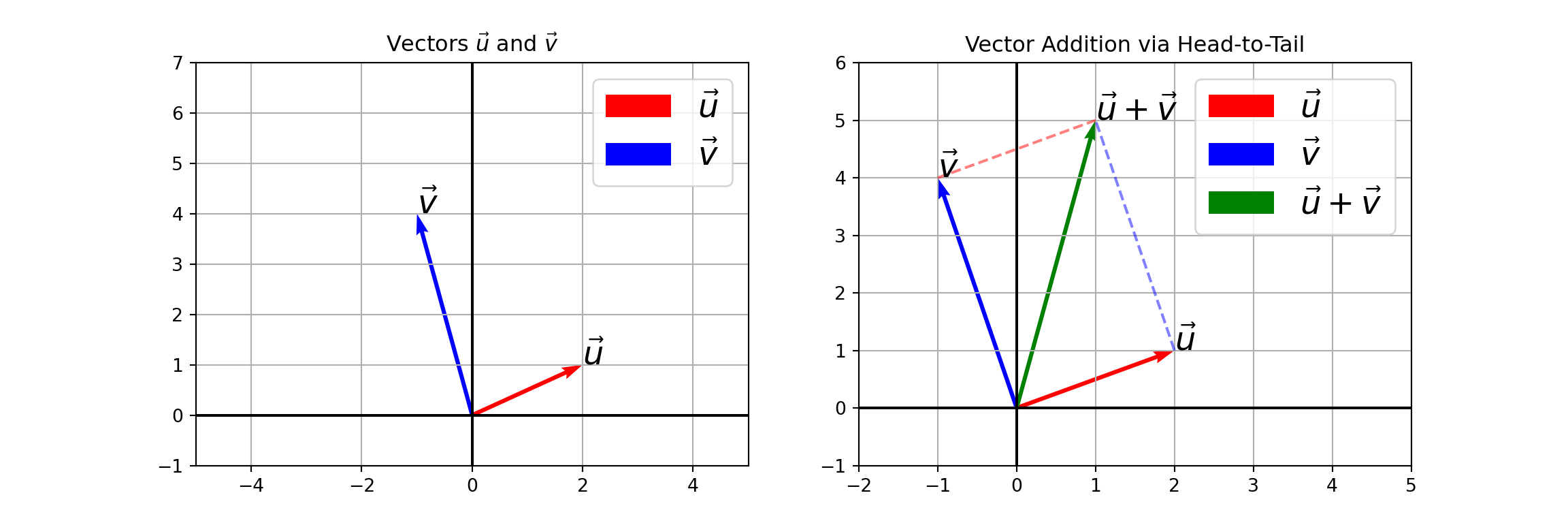
Geometry of Vector Addition
- We often say that vector addition is conducted head to tail.
- This phrase refers to the geometry of vector addition.
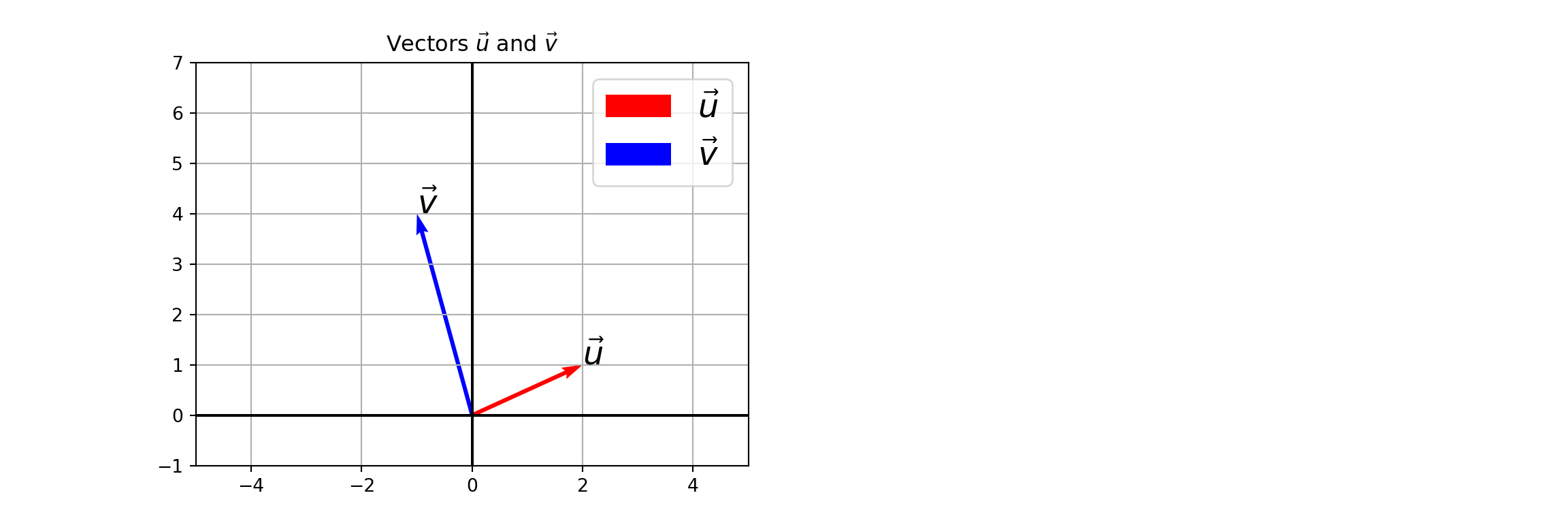
- Consider the plots below which shows the sum of the vectors \(\vec{u}\) and \(\vec{v}\) where \(\vec{u} = \begin{bmatrix} 2\\ 1\end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} -1\\ 4\end{bmatrix}\).
Geometry of Vector Addition
- We often say that vector addition is conducted head to tail.
- This phrase refers to the geometry of vector addition.
- Consider the plots below which shows the sum of the vectors \(\vec{u}\) and \(\vec{v}\) where \(\vec{u} = \begin{bmatrix} 2\\ 1\end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} -1\\ 4\end{bmatrix}\).
Scalar Multiplication
Multiplying a vector by a scalar stretches, shrinks, and/or reflects the vector. For example if \(a\) is a scalar and \(\vec{v}\) is a vector, then
\[a \vec{v} = \begin{bmatrix} a v_1 \\ a v_2\\ \vdots\\ av_n \end{bmatrix}\]
Example: Consider the vector \(\vec{v} = \begin{bmatrix} 2\\ 1\end{bmatrix}\) and scalars \(a_1 = 3\), \(a_2 = 0.5\), and \(a_3 = -1.5\).
- \(a_1\vec{v} = 3\begin{bmatrix} 2\\ 1\end{bmatrix} = \begin{bmatrix} 3\left(2\right)\\ 3\left(1\right)\end{bmatrix} = \begin{bmatrix} 6\\ 3\end{bmatrix}\)
- Find \(a_2\vec{v}\)
- Find \(a_3\vec{v}\)
Scalar Multiplication
Example: Consider the vector \(\vec{v} = \begin{bmatrix} 2\\ 1\end{bmatrix}\) and scalars \(a_1 = 3\), \(a_2 = 0.5\), and \(a_3 = -1.5\).
- \(a_1\vec{v} = 3\begin{bmatrix} 2\\ 1\end{bmatrix} = \begin{bmatrix} 3\left(2\right)\\ 3\left(1\right)\end{bmatrix} = \begin{bmatrix} 6\\ 3\end{bmatrix}\)
- Find \(a_2\vec{v}\)
- Find \(a_3\vec{v}\)
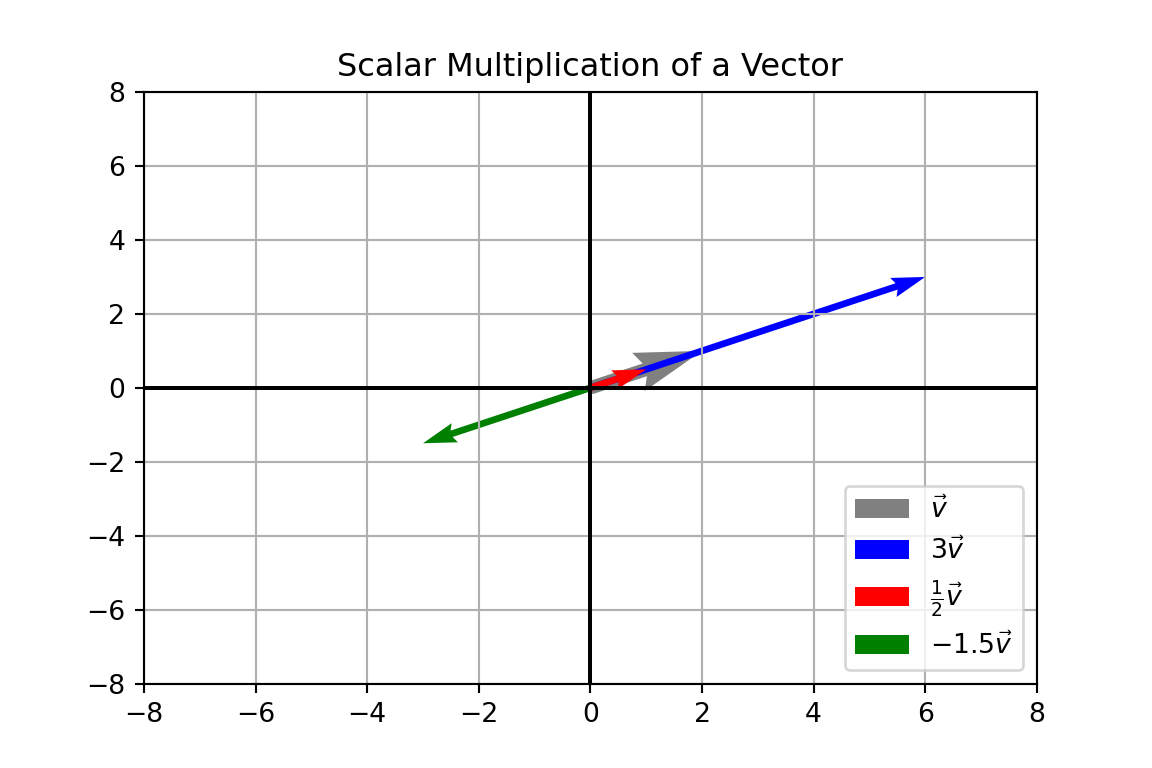
Scalar Multiplication (Additional Examples)
Example: Consider the vectors \(\vec{u} = \begin{bmatrix} 9\\ 0\\ 3\end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} -12\\ -6\end{bmatrix}\), along with scalars \(a_1 = -3\) and \(a_2 = 1/3\). Construct the following vectors.
\[(i)~~a_1\vec{u}~~~~~~~~(ii)~~a_1\vec{v}~~~~~~~~(iii)~~a_2\vec{u}~~~~~~~~(iv)~~a_2\vec{v}\]
Vector Multiplication?
We can define multiple types of vector products here.
- Haddamard Product: An Element-wise product, not used in MAT350 but used heavily in machine learning, AI, signal processing, and probabilistic modeling
- Inner Product or Dot Product
- Cross-Product
- Outer Product
Inner Product / Dot Product
Dot Product: Given two vectors \(\vec{u}\) and \(\vec{v}\) of the same size, we can define the dot product of \(\vec{u}\) and \(\vec{v}\) to be
\[\vec{u}\cdot \vec{v} = \begin{bmatrix} u_1\\ u_2\\ \vdots\\ u_n\end{bmatrix}\cdot \begin{bmatrix} v_1\\ v_2\\ \vdots\\ v_n\end{bmatrix} = u_1v_1 + u_2v_2 + \cdots + u_nv_n\]
Inner Product / Dot Product
Dot Product: Given two vectors \(\vec{u}\) and \(\vec{v}\) of the same size, we can define the dot product of \(\vec{u}\) and \(\vec{v}\) to be
\[\vec{u}\cdot \vec{v} = u_1v_1 + u_2v_2 + \cdots + u_nv_n\]
Example: For each pair of vectors below, compute the dot product.
- Given \(\vec{u_1} = \begin{bmatrix} 2\\ -3\end{bmatrix}\) and \(\vec{u_2} = \begin{bmatrix} 8\\ -4\end{bmatrix}\), the dot product \(\vec{u_1}\cdot\vec{u_2}\) is…
\[\vec{u_1} \cdot \vec{u_2} = 2\left(8\right) + \left(-3\right)\left(-4\right) = 16 + 12 = 28\]
- Given \(\vec{v_1} = \begin{bmatrix} -9\\ 7\\ 0\\ 1\end{bmatrix}\) and \(\vec{v_2} = \begin{bmatrix} 1\\ -1\\ 5\\ -2\end{bmatrix}\), the dot product \(\vec{v_1}\cdot \vec{v_2}\) is…
Inner Product / Dot Product
Dot Product: Given two vectors \(\vec{u}\) and \(\vec{v}\) of the same size, we can define the dot product of \(\vec{u}\) and \(\vec{v}\) to be
\[\vec{u}\cdot \vec{v} = u_1v_1 + u_2v_2 + \cdots + u_nv_n\]
We’ll find many uses for the dot product between two vectors. For example,
- the dot product between a vector and itself gives the square of the magnitude (length) of the vector.
\[\vec{x}\cdot\vec{x} = x_1^2 + x_2^2 + \cdots + x_n^2 = \left|\left|\vec{x}\right|\right|^2\]
So, \(\left|\left|\vec{x}\right|\right| = \sqrt{\vec{x}\cdot\vec{x}}\)
Example: Find the magnitude of each vector \(\vec{u} = \begin{bmatrix} 3\\ 4\end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} 1\\ -3\\ 5\end{bmatrix}\)
Inner Product / Dot Product
Dot Product: Given two vectors \(\vec{u}\) and \(\vec{v}\) of the same size, we can define the dot product of \(\vec{u}\) and \(\vec{v}\) to be
\[\vec{u}\cdot \vec{v} = u_1v_1 + u_2v_2 + \cdots + u_nv_n\]
We’ll find many uses for the dot product between two vectors. For example,
- the dot product between two vectors \(\vec{u}\) and \(\vec{v}\) can be used to determine the angle (\(\theta\)) between the vectors
\[\cos\left(\theta\right) = \frac{\vec{u}\cdot\vec{v}}{||\vec{u}||||\vec{v}||}\]
Inner Product / Dot Product
Dot Product: Given two vectors \(\vec{u}\) and \(\vec{v}\) of the same size, we can define the dot product of \(\vec{u}\) and \(\vec{v}\) to be
\[\vec{u}\cdot \vec{v} = u_1v_1 + u_2v_2 + \cdots + u_nv_n\]
We’ll find many uses for the dot product between two vectors. For example,
- the dot product between two vectors \(\vec{u}\) and \(\vec{v}\) can be used to determine the angle (\(\theta\)) between the vectors
\[\cos\left(\theta\right) = \frac{\vec{u}\cdot\vec{v}}{||\vec{u}||||\vec{v}||}\]
Which is particularly useful to quickly determine whether two vectors are orthogonal (they meet at a \(90^\circ\) angle).
Example: Determine whether \(\vec{u} = \begin{bmatrix} 1\\ 3\\ 11\end{bmatrix}\) and \(\vec{v} = \begin{bmatrix} -4\\ 5\\ -1\end{bmatrix}\) are orthogonal.
Cross Product (3D only)
Cross Product: When in three dimensions, we can define the cross product between two vectors \(\vec{u}\) and \(\vec{v}\).
\[\vec{u} \times \vec{v} = \begin{bmatrix} u_1\\ u_2\\ u_3\end{bmatrix}\times \begin{bmatrix} v_1\\ v_2\\ v_3\end{bmatrix} = \begin{bmatrix} u_2 v_3 - u_3 v_2 \\ u_3 v_1 - u_1 v_3 \\ u_1 v_2 - u_2 v_1 \end{bmatrix}\]
- The result of taking the cross product is a new vector \(\vec{w}\) which is orthogonal (perpendicular) to both \(\vec{u}\) and \(\vec{v}\).
Note: Since there are two opposing directions such a vector could point in, we use the “right-hand rule” to determine which direction the cross-product points.
Example: For each pair of vectors below, compute the cross-product.
- \(\vec{e_1} = \begin{bmatrix} 1\\ 0\\ 0\end{bmatrix}\) and \(\vec{e_2} = \begin{bmatrix} 0\\ 1\\ 0\end{bmatrix}\)
- \(\vec{v_1} = \begin{bmatrix} 1\\ -2\\ -1\end{bmatrix}\) and \(\vec{v_2} = \begin{bmatrix} 0\\ 4\\ 12\end{bmatrix}\)
Outer Product
. . .
There’s an additional vector product, called an outer-product, but we’ll wait until we discuss matrices next time in order to define it.
. . .
We’ll also briefly revisit the inner-product at that time.
Divide and… Nope
While division exists for scalars, and we’ve taken advantage of it as an operation that “undoes” multiplication, division by vectors is not a defined operation.
Vector Norms
- Norms are generally used to measure the size or magnitude of the object that they are applied to.
- One norm you are familiar with is the absolute value function for real numbers.
- We can define lots of norms for objects, but for vectors in Linear Algebra, we’ll be interested in the \(\ell_2\) (or Euclidean) norm, which we encountered a few slides ago.
The \(\ell_2\) (Euclidean) norm of a vector \(\vec{v}\) measures its magnitude, and is given by
\[\|\vec{v}\| = \sqrt{\left(\vec{v}\cdot\vec{v}\right)} = \sqrt{\left(v_1^2 + v_2^2 + \cdots + v_n^2\right)}\]
Example: You saw two examples when we first encountered the inner-product, but calculate the length of the vector \(\vec{v} = \begin{bmatrix} 2\\ 0\\ -4\\ 5\end{bmatrix}\) for practice.
Special Vectors
With the vector operations defined above, we can define a few special classes of vector that we’ll encounter later in our course (but that you may have already encountered elsewhere).
Unit Vectors: A vector of magnitude \(1\), that is a vector \(\vec{v}\) such that \(||\vec{v}|| = 1\), is called a unit vector.
Constructing a Unit Vector: Given any vector \(\vec{w}\), which is not the zero-vector, we can construct the unit vector pointing in the direction of \(\vec{w}\) using
\[\vec{u_w} = \frac{\vec{w}}{||\vec{w}||}\]
Example: Given the vector \(\vec{v} = \begin{bmatrix} 2\\ 8\\ -3\end{bmatrix}\), construct a unit vector pointing in the same direction as \(\vec{v}\).
Special Vectors
With the vector operations defined so far, we can define a few special classes of vector that we’ll encounter later in our course (but that you may have already encountered elsewhere).
Normal Vectors: A vector \(\vec{n}\) that is orthogonal (perpendicular) to a surface or another vector is called a normal vector.
To find vectors normal to a given vector, we remember that \(\vec{v}\) and \(\vec{n}\) are orthogonal if \(\vec{v}\cdot \vec{n} = 0\).
Examples: We’ll wait on the construction of orthogonal/normal vectors for now, but…
- given a single vector, we can use the fact that the dot product between that vector and a vector normal to it will be \(0\).
- given a single vector, we can multiply by an appropriate rotation matrix in order to obtain a vector normal to the original.
- we can use the cross-product to construct a vector orthogonal to two vectors in three dimensions.
- you can also use a procedure called the Gram-Schmidt orthogonalization process
Summary
We’ve covered quite a bit of ground here, including how to…
add and subtract vectors of compatible size
compute different types of products involving vectors
- scalar multiplication
- inner products
- cross products
- outer products
calculate the magnitude (length, or \(\ell_2\)-norm) of a vector
determine the angle between two vectors, including whether two vectors are orthogonal
identify and construct unit vectors
identify normal vectors
Homework
\[\Huge{\text{Start Homework 1}}\] \[\Huge{\text{on MyOpenMath}}\]
Next Time…
\(\Huge{\text{Matrices and Arithmetic}}\)