MAT 350: Diagonalization

Dr. Gilbert

August 16, 2025

Warm-Up Problems

Complete the following warm-up problems to re-familiarize yourself with concepts we’ll be leveraging today.

Example: Consider the matrix \(A = \begin{bmatrix} 3 & 0\\ 0 & -1\end{bmatrix}\), along with the vectors \(\vec{e_1} = \begin{bmatrix} 1\\ 0\end{bmatrix}\) and \(\vec{e_2} = \begin{bmatrix} 0\\ 1\end{bmatrix}\). Calculate \(A\vec{e_1}\) and \(A\vec{e_2}\).

Example: Consider the matrix \(B = \begin{bmatrix} 1 & 2\\ 2 & 1\end{bmatrix}\), along with the vectors \(\vec{v_1} = \begin{bmatrix} 1\\ 1\end{bmatrix}\) and \(\vec{v_2} = \begin{bmatrix} -1\\ 1\end{bmatrix}\). Compute \(B\vec{v_1}\) and \(B\vec{v_2}\).

Motivation for Today

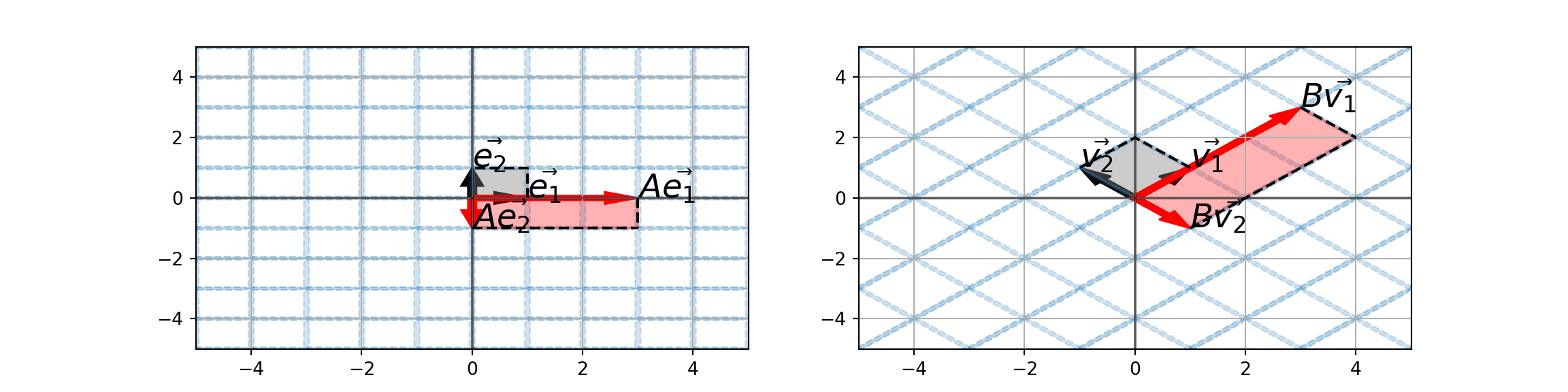
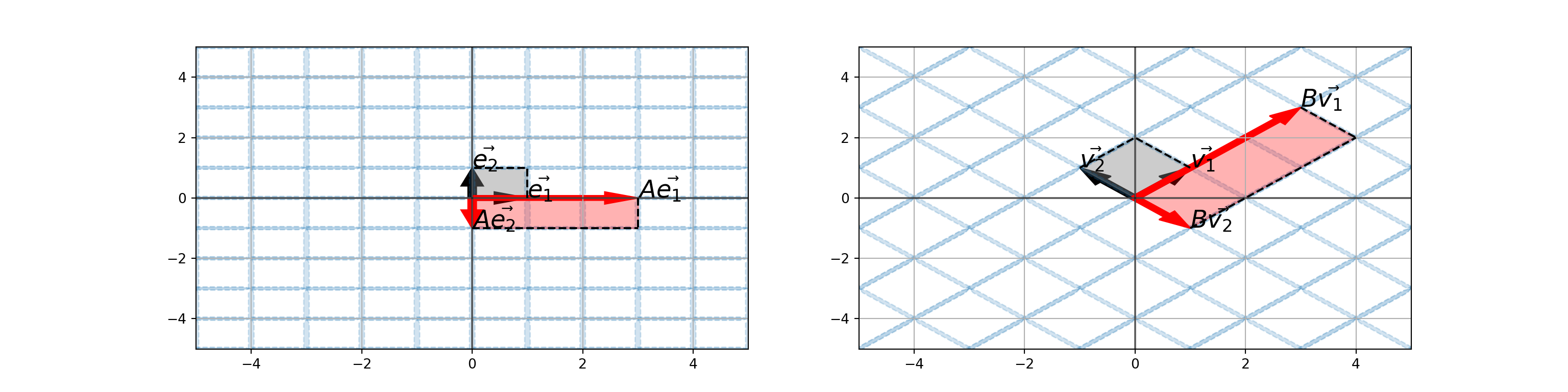
Consider the matrices \(A = \begin{bmatrix} 3 & 0\\ 0 & -1\end{bmatrix}\) and the matrix \(B = \begin{bmatrix} 1 & 2\\ 2 & 1\end{bmatrix}\).

1. How does the matrix \(A\) act on the vectors \(\vec{e_1} = \begin{bmatrix} 1\\ 0\end{bmatrix}\) and \(\vec{e_2} = \begin{bmatrix} 0\\ 1\end{bmatrix}\)?
2. How does the matrix \(B\) act on the vectors \(\vec{v_1} = \begin{bmatrix} 1\\ 1\end{bmatrix}\) and \(\vec{v_2} = \begin{bmatrix} -1\\ 1\end{bmatrix}\).

In particular, we’re interested in the parallelograms resulting from the vectors \(A\vec{e_1}\) and \(A\vec{e_2}\) as well as the vectors \(B\vec{v_1}\) and \(B\vec{v_2}\).

Motivation for Today

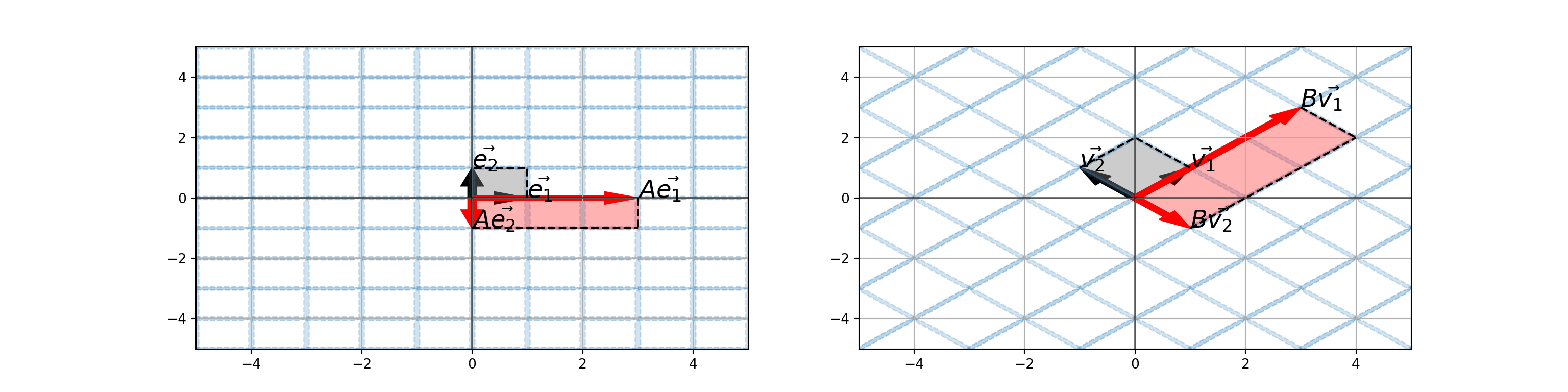
• The matrix \(A = \begin{bmatrix} 3 & 0\\ 0 & -1\end{bmatrix}\) stretches vectors in the direction of \(\vec{e_1}\) by \(3\) and flips vectors in the opposite direction of \(\vec{e_2}\).

• Similarly, the matrix \(B = \begin{bmatrix} 1 & 2\\ 2 & 1\end{bmatrix}\) stretches vectors in the \(\vec{v_1}\) direction by \(3\) and flips vectors in the opposite direction of \(\vec{v_2}\).

  • This must mean that, at least in some sense, the matrices \(A\) and \(B\) are related.
  • The matrix \(B\) does what the matrix \(A\) does, just in a different basis.

Motivation for Today

1. Is the observed relationship between the matrices \(A\) and \(B\) coincidence?

2. Is it luck?

3. Given some generic matrix like \(B\), can we obtain a convenient matrix like \(A\) which has analogous geometric effects to \(B\), but where those geometric effects are easily identified?

   • When, and how, is such a discovery possible?

Reminders and Today’s Goal

• We can think of matrix-vector multiplication \(A\vec{x}\) as calculating a linear combination of the columns of the matrix.

\[\begin{bmatrix} \vec{a_1} & \vec{a_2} & \cdots & \vec{a_n}\end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n\end{bmatrix} = \begin{bmatrix} x_1\vec{a_1} + x_2\vec{a_2} + \cdots + x_n\vec{a_n}\end{bmatrix}\]

• We can think of matrix multiplication \(BA\) as a transformation of the columns of the matrix \(A\).

\[B\begin{bmatrix} \vec{a_1} & \vec{a_2} & \cdots & \vec{a_n}\end{bmatrix} = \begin{bmatrix} B\vec{a_1} & B\vec{a_2} & \cdots & B\vec{a_n}\end{bmatrix}\]

Reminders and Today’s Goal

• The non-zero vector \(\vec{v}\) is an eigenvector of the matrix \(A\) if \(A\vec{v} = \lambda \vec{v}\) for some \(\lambda\).

  • With eigenvectors, matrix multiplication is simplified to just scalar multiplication.

• If a matrix has \(n\) distinct eigenvalues, then it is possible to find a basis for \(\mathbb{R}^n\) consisting of eigenvectors (an eigenbasis).

  • Note. There are lots of scenarios other than this one where the existence of an eigenbasis can be guaranteed. In this notebook, we’ll simply assume that we are in such a scenario.

Goals for Today: After today’s discussion, you should be able to

• Define and identify similar matrices
• Outline and execute the diagonalization procedure for “diagonalizable” matrices
• Identify and discuss the connections between eigenvectors, eigenvalues, and diagonalization

A Note on Discussion Structure

We’re about to introduce the notion of diagonalization of a matrix.

We’ll alternate between the following two scenarios.

• General claims and observations about an \(n\times n\) matrix with an eigenbasis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) and corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\) and
• A more concrete example using the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = -6\).

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Construct the matrix \(P = \begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix}\), and consider the product \(AP\)…

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Construct the matrix \(P = \begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix}\), and consider the product \(AP\)…

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

Consider the matrix \(P = \begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\) and compute \(AP\)…

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[AP = A\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[AP = A\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = A\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[AP = A\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix} = \begin{bmatrix} A\vec{v_1} & A\vec{v_2} & \cdots & A\vec{v_n}\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = A\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[AP = A\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix} = \begin{bmatrix} A\vec{v_1} & A\vec{v_2} & \cdots & A\vec{v_n}\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = A\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix} = \begin{bmatrix} A\begin{bmatrix} 1\\ 1\end{bmatrix} & A\begin{bmatrix} 2\\ -1\end{bmatrix}\end{bmatrix}\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[AP = A\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix} = \begin{bmatrix} A\vec{v_1} & A\vec{v_2} & \cdots & A\vec{v_n}\end{bmatrix}\]

\[= \begin{bmatrix}\lambda_1\vec{v_1} & \lambda_2\vec{v_2} & \cdots & \lambda_n\vec{v_n}\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = A\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix} = \begin{bmatrix} A\begin{bmatrix} 1\\ 1\end{bmatrix} & A\begin{bmatrix} 2\\ -1\end{bmatrix}\end{bmatrix}\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[AP = A\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix} = \begin{bmatrix} A\vec{v_1} & A\vec{v_2} & \cdots & A\vec{v_n}\end{bmatrix}\]

\[= \begin{bmatrix}\lambda_1\vec{v_1} & \lambda_2\vec{v_2} & \cdots & \lambda_n\vec{v_n}\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = A\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix} = \begin{bmatrix} A\begin{bmatrix} 1\\ 1\end{bmatrix} & A\begin{bmatrix} 2\\ -1\end{bmatrix}\end{bmatrix} = \begin{bmatrix}3\begin{bmatrix} 1\\ 1\end{bmatrix} & -6\begin{bmatrix}2\\ -1\end{bmatrix}\end{bmatrix}\]

\[= \begin{bmatrix} 3 & -12\\ 3 & 6\end{bmatrix}\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Consider the matrix \(P = \begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix}\) again, along with the diagonal matrix \(D\), whose entries are the eigenvalues of \(A\). Compute the product \(PD\)

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Consider the matrix \(P = \begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix}\) again, along with the diagonal matrix \(D\), whose entries are the eigenvalues of \(A\). Compute the product \(PD\)

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

Consider the matrix \(P = \begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\) and the diagonal matrix \(D = \begin{bmatrix} 3 & 0\\ 0 & -6\end{bmatrix}\). Compute \(PD\)…

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[PD = \begin{bmatrix}\vec{v_1} & \vec{v_2} & \cdots & \vec{v_n}\end{bmatrix}\begin{bmatrix}\lambda_1 & 0 & \cdots & 0\\ 0 & \lambda_2 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & \lambda_n\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

Consider the matrix \(P = \begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\) and the diagonal matrix \(D = \begin{bmatrix} 3 & 0\\ 0 & -6\end{bmatrix}\). Compute \(PD\)…

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[PD = \begin{bmatrix} \lambda_1\vec{v_1} & \lambda_2\vec{v_2} & \cdots & \lambda_n\vec{v_n}\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

Consider the matrix \(P = \begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\) and the diagonal matrix \(D = \begin{bmatrix} 3 & 0\\ 0 & -6\end{bmatrix}\). Compute \(PD\)…

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[PD = \begin{bmatrix} \lambda_1\vec{v_1} & \lambda_2\vec{v_2} & \cdots & \lambda_n\vec{v_n}\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[PD = \begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\begin{bmatrix} 3 & 0\\ 0 & -6\end{bmatrix}\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

\[PD = \begin{bmatrix} \lambda_1\vec{v_1} & \lambda_2\vec{v_2} & \cdots & \lambda_n\vec{v_n}\end{bmatrix}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[PD = \begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\begin{bmatrix} 3 & 0\\ 0 & -6\end{bmatrix} = \begin{bmatrix} 3 & -12\\ 3 & 6\end{bmatrix}\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Notice that

\[AP = \begin{bmatrix} \lambda_1\vec{v_1} & \lambda_2\vec{v_2} & \cdots & \lambda_n\vec{v_n}\end{bmatrix} = PD\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[PD = \begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\begin{bmatrix} 3 & 0\\ 0 & -6\end{bmatrix} = \begin{bmatrix} 3 & -12\\ 3 & 6\end{bmatrix}\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Notice that

\[AP = \begin{bmatrix} \lambda_1\vec{v_1} & \lambda_2\vec{v_2} & \cdots & \lambda_n\vec{v_n}\end{bmatrix} = PD\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = \begin{bmatrix} 3 & -12\\ 3 & 6\end{bmatrix} = PD\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Notice that

\[\begin{align} AP &= PD \end{align}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = \begin{bmatrix} 3 & -12\\ 3 & 6\end{bmatrix} = PD\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Notice that

\[\begin{align} AP &= PD\\ \implies \left(AP\right)P^{-1} &= \left(PD\right)P^{-1} \end{align}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = \begin{bmatrix} 3 & -12\\ 3 & 6\end{bmatrix} = PD\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Notice that

\[\begin{align} AP &= PD\\ \implies \left(AP\right)P^{-1} &= \left(PD\right)P^{-1}\\ \implies A\left(PP^{-1}\right) &= PDP^{-1} \end{align}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = \begin{bmatrix} 3 & -12\\ 3 & 6\end{bmatrix} = PD\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Notice that

\[\begin{align} AP &= PD\\ \implies \left(AP\right)P^{-1} &= \left(PD\right)P^{-1}\\ \implies A\left(PP^{-1}\right) &= PDP^{-1}\\ \implies A &= PDP^{-1} \end{align}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = \begin{bmatrix} 3 & -12\\ 3 & 6\end{bmatrix} = PD\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Notice that

\[A = PDP^{-1}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

\[AP = \begin{bmatrix} 3 & -12\\ 3 & 6\end{bmatrix} = PD\]

Diagonalization

General Case: Suppose we have an \(n\times n\) matrix \(A\) and a corresponding basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with corresponding eigenvalues \(\lambda_1,~\lambda_2,~\cdots,~\lambda_n\).

Notice that

\[A = PDP^{-1}\]

Example: Suppose we have the \(2\times 2\) matrix \(A = \begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix}\) with eigenbasis \(\left\{\begin{bmatrix} 1\\ 1\end{bmatrix}, \begin{bmatrix} 2\\ -1\end{bmatrix}\right\}\) and corresponding eigenvalues \(\lambda_1 = 3\) and \(\lambda_2 = 6\).

So,

\[\begin{bmatrix} -3 & 6\\ 3 & 0\end{bmatrix} = \begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\begin{bmatrix} 3 & 0\\ 0 & -6\end{bmatrix}\left(\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\right)^{-1}\]

Diagonalization…So What?

Summary (Diagonalization of \(A\)): If \(A\) is an \(n\times n\) matrix and there exists a basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with associated eigenvalues \(\lambda_1,~\lambda_2,~ \cdots,~lambda_n\), then we can write \(A = PDP^{-1}\) where the columns of the matrix \(P\) are the eigenvectors and \(D\) is a diagonal matrix with the corresponding eigenvalues along its diagonal.

Punchline: To connect back to the images we began this notebook with, if the matrix \(A\) is diagonalizable as \(A = PDP^{-1}\), then the effect of multiplying a vector by \(A\), viewed in the basis defined by the columns of \(P\), is the same effect as multiplying by \(D\) with the standard basis.

Example: So when we rewrite the matrix \(A\) as

Diagonalization…So What?

Summary (Diagonalization of \(A\)): If \(A\) is an \(n\times n\) matrix and there exists a basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with associated eigenvalues \(\lambda_1,~\lambda_2,~ \cdots,~lambda_n\), then we can write \(A = PDP^{-1}\) where the columns of the matrix \(P\) are the eigenvectors and \(D\) is a diagonal matrix with the corresponding eigenvalues along its diagonal.

Punchline: To connect back to the images we began this notebook with, if the matrix \(A\) is diagonalizable as \(A = PDP^{-1}\), then the effect of multiplying a vector by \(A\), viewed in the basis defined by the columns of \(P\), is the same effect as multiplying by \(D\) with the standard basis.

Example: So when we rewrite the matrix \(A\) as

\[\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\begin{bmatrix} 3 & 0\\ 0 & -6\end{bmatrix}\left(\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\right)^{-1}\]

Diagonalization…So What?

Summary (Diagonalization of \(A\)): If \(A\) is an \(n\times n\) matrix and there exists a basis \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_n}\right\}\) for \(\mathbb{R}^n\) consisting of eigenvectors of \(A\) with associated eigenvalues \(\lambda_1,~\lambda_2,~ \cdots,~lambda_n\), then we can write \(A = PDP^{-1}\) where the columns of the matrix \(P\) are the eigenvectors and \(D\) is a diagonal matrix with the corresponding eigenvalues along its diagonal.

Punchline: To connect back to the images we began this notebook with, if the matrix \(A\) is diagonalizable as \(A = PDP^{-1}\), then the effect of multiplying a vector by \(A\), viewed in the basis defined by the columns of \(P\), is the same effect as multiplying by \(D\) with the standard basis.

Example: So when we rewrite the matrix \(A\) as

\[\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\begin{bmatrix} 3 & 0\\ 0 & -6\end{bmatrix}\left(\begin{bmatrix} 1 & 2\\ 1 & -1\end{bmatrix}\right)^{-1}\]

We see that \(A\)

1. stretches vectors by a factor of \(3\) in the direction of its first eigenvector.
2. flips vectors across its second eigenvector and stretches them by a factor of \(6\).

Aside: Computing Powers of Matrices

• Matrix multiplication is an arduous process because of the number of operations involved.

• Often times we are interested in what happens when a matrix repeatedly acts upon a vector though.

  • This is particularly the case when we are considering state transition matrices as part of dynamical systems or Markov chains.
  • If \(A\) is a transition matrix and we start from an initial state vector \(\vec{x}\), we may want to consider the state in \(100\) time steps.
  • This requires that we compute \(A^{100}\vec{x}\), which is * a lot* of matrix multiplication!

I’ll show two strategies for calculating powers of matrices on the next slide.

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1} \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100} \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right) \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1} \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Otherwise…

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Otherwise…

\[\begin{align} A^2 &= AA \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Otherwise…

\[\begin{align} A^2 &= AA\\ A^4 &= \left(A^2\right)\left(A^2\right) \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Otherwise…

\[\begin{align} A^2 &= AA\\ A^4 &= \left(A^2\right)\left(A^2\right)\\ A^8 &= \left(A^4\right)\left(A^4\right) \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Otherwise…

\[\begin{align} A^2 &= AA\\ A^4 &= \left(A^2\right)\left(A^2\right)\\ A^8 &= \left(A^4\right)\left(A^4\right)\\ A^{16} &= \left(A^8\right)\left(A^8\right) \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Otherwise…

\[\begin{align} A^2 &= AA\\ A^4 &= \left(A^2\right)\left(A^2\right)\\ A^8 &= \left(A^4\right)\left(A^4\right)\\ A^{16} &= \left(A^8\right)\left(A^8\right)\\ A^{32} &= \left(A^{16}\right)\left(A^{16}\right) \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Otherwise…

\[\begin{align} A^2 &= AA\\ A^4 &= \left(A^2\right)\left(A^2\right)\\ A^8 &= \left(A^4\right)\left(A^4\right)\\ A^{16} &= \left(A^8\right)\left(A^8\right)\\ A^{32} &= \left(A^{16}\right)\left(A^{16}\right)\\ A^{64} &= \left(A^{32}\right)\left(A^{32}\right) \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Otherwise…

\[\begin{align} A^2 &= AA\\ A^4 &= \left(A^2\right)\left(A^2\right)\\ A^8 &= \left(A^4\right)\left(A^4\right)\\ A^{16} &= \left(A^8\right)\left(A^8\right)\\ A^{32} &= \left(A^{16}\right)\left(A^{16}\right)\\ A^{64} &= \left(A^{32}\right)\left(A^{32}\right)\\ A^{100} &= \left(A^{64}\right)\left(A^{32}\right)\left(A^4\right) \end{align}\]

Aside: Computing Powers of Matrices

Let’s consider the task of trying to compute \(A^{100}\) for some matrix \(A\).

If \(A\) is Diagonalizable…

\[\begin{align} A &= PDP^{-1}\\ \implies A^{100} &= \left(PDP^{-1}\right)^{100}\\ &= \left(PDP^{-1}\right)\left(PDP^{-1}\right)\cdots\left(PDP^{-1}\right)\\ &= PD\left(P^{-1}P\right)D\left(P^{-1}P\right)\cdots \left(P^{-1}P\right)DP^{-1}\\ &= PD^{100}P^{-1} \end{align}\]

Because \(D\) is a diagonal matrix, \(D^{100}\) is obtained by raising its diagonal entries to the \(100^{\text{th}}\) power.

Instead of 100 matrices, we only need to multiply three.

Otherwise…

\[\begin{align} A^2 &= AA\\ A^4 &= \left(A^2\right)\left(A^2\right)\\ A^8 &= \left(A^4\right)\left(A^4\right)\\ A^{16} &= \left(A^8\right)\left(A^8\right)\\ A^{32} &= \left(A^{16}\right)\left(A^{16}\right)\\ A^{64} &= \left(A^{32}\right)\left(A^{32}\right)\\ A^{100} &= \left(A^{64}\right)\left(A^{32}\right)\left(A^4\right) \end{align}\]

Eight matrix multiplications is better than a hundred!

Examples to Try

Example 1: Determine whether the following matrices are diagonalizable and, if so, find matrices \(P\) and \(D\) such that \(A = PDP^{-1}\).

\[(i)~~A_1 = \begin{bmatrix} -2 & -2\\ -2 & 1\end{bmatrix}~~~~~(ii)~~A_2 = \begin{bmatrix} -1 & 1\\ -1 & -3\end{bmatrix}\]

\[(iii)~~A_3 = \begin{bmatrix} 1 & 0 & 0\\ 2 & -2 & 0\\ 0 & 1 & 4\end{bmatrix}~~~~~(iv)~~A_4 = \begin{bmatrix} 1 & 2 & 2\\ 2 & 1 & 2\\ 2 & 2 & 1\end{bmatrix}\]

Example 2: Describe the geometric effect that the following matrices have in \(\mathbb{R}^2\).

\[(i)~~A_1 = \begin{bmatrix} 2 & 0 \\ 0 & 2\end{bmatrix}~~~~~(ii)~~A_2 = \begin{bmatrix}4 & 2\\ 0 & 4\end{bmatrix}~~~~~(iii)~~A_3 = \begin{bmatrix} 3 & -6\\ 6 & 3\end{bmatrix}\]

\[(iv)~~A_4 = \begin{bmatrix} 4 & 0\\ 0 & -2\end{bmatrix}~~~~~(v)~~A_5 = \begin{bmatrix} 1 & 3\\ 3 & 1\end{bmatrix}\]

Homework

\[\Huge{\text{Optional Homework 12}}\] \[\Huge{\text{on MyOpenMath}}\]

Next Time…

\(\Huge{\text{Discrete Dynamical}}\)

\(\Huge{\text{Systems}}\)