MAT 350: Subspaces

Dr. Gilbert

August 13, 2025

Warm-Up Problems

Complete the following warm-up problems to re-familiarize yourself with concepts we’ll be leveraging today.

Example: Determine whether the vectors \(\vec{v_1} = \left[\begin{array}{r} 2\\ 1\\ -1\end{array}\right]\), \(\vec{v_2} = \left[\begin{array}{r} 1\\ 1\\ 0\end{array}\right]\), and \(\vec{v_3} = \left[\begin{array}{r} 1\\ 3\\ 1\end{array}\right]\) are linearly independent.

Example: Construct the inverse of the matrix \(A = \left[\begin{array}{rrr} 1 & 5 & 2\\ 0 & -1 & 3\\ 1 & 0 & 1\end{array}\right]\) if it exists.

Reminders and Today’s Goal

The space \(\mathbb{R}^n\) is the space consisting of all \(n\)-component vectors whose entries are real numbers.
- That is, \(\mathbb{R}^n = \left\{\begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n\end{bmatrix}~\mid~ x_i\in\mathbb{R}\right\}\)
The zero vector (\(\vec{0}\)) is a vector whose entries are all \(0\)’s.
The span of a set of vectors, \(\text{span}\left(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_p}\right\}\right)\) is the set of all linear combinations of the vectors \(\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_p}\).
- The zero vector is in the span of any non-empty collection of vectors.
A basis for a space is a linearly independent collection of vectors which span the space.
- A collection of vectors span a space if every vector in the space can be written as a linear combination of vectors from the collection.
The vector \(\vec{y}\) is a linear combination of the vectors \(V = \left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_p}\right\}\) if \(\vec{y}\) can be written as a linear combination of the vectors in \(V\).
- That is, \(\vec{y} = c_1\vec{v_1} + c_2\vec{v_2} + \cdots + c_p\vec{v_p}\) for some scalars \(c_1,~c_2,~\cdots,~c_p\)

Reminders and Today’s Goal

Goals for Today: After today’s discussion, you should be able to

define subspaces via the subspace criteria
determine whether a collection of vectors qualifies as a subspace
identify connections of subspaces to solution sets of vector equations, matrix equations, and linear systems

The Subspace Criteria

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Note: Items (2.) and (3.) in the definition above are often described as the subspace being closed under addition and scalar multiplication.

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Note that \(\vec{0}\in \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) since \(\vec{0} = 0\cdot\left[\begin{array}{r} 1\\ -3\end{array}\right]\). \(\checkmark\)

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Let \(\vec{x}\) and \(\vec{y}\) be in \(\text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\).
Then, there exist scalars \(c_1\) and \(c_2\) such that \(\vec{x} = c_1\left[\begin{array}{r} 1\\ -3\end{array}\right]\) and \(\vec{y} = c_2\left[\begin{array}{r} 1\\ -3\end{array}\right]\).

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Now, notice that

\[\begin{align*} \vec{x} + \vec{y} \end{align*}\]

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Now, notice that

\[\begin{align*} \vec{x} + \vec{y} &= c_1\left[\begin{array}{r} 1\\ -3\end{array}\right] + c_2\left[\begin{array}{r} 1\\ -3\end{array}\right] \end{align*}\]

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Now, notice that

\[\begin{align*} \vec{x} + \vec{y} &= c_1\left[\begin{array}{r} 1\\ -3\end{array}\right] + c_2\left[\begin{array}{r} 1\\ -3\end{array}\right] = \left(c_1 + c_2\right)\left[\begin{array}{r} 1\\ -3\end{array}\right] \end{align*}\]

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Now, notice that

But \(c_1 + c_2\) is just another scalar, which we can call \(c_3\), so \(\vec{x} + \vec{y}\in H~\checkmark\)

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Let \(\vec{v}\in \text{span}\left(\left\{\begin{bmatrix} 1\\ -3\end{bmatrix}\right\}\right)\) and \(c \in \mathbb{R}\) be a scalar.
Then there exists some scalar \(c_1\) so that \(\vec{v} = c_1\begin{bmatrix} 1\\ -3\end{bmatrix}\)

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Now, notice that

\[\begin{align*} c\vec{v} \end{align*}\]

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Now, notice that

\[\begin{align*} c\vec{v} &= c\left(c_1\begin{bmatrix} 1\\ -3\end{bmatrix}\right) \end{align*}\]

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Now, notice that

\[\begin{align*} c\vec{v} &= c\left(c_1\begin{bmatrix} 1\\ -3\end{bmatrix}\right) = \left(c\cdot c_1\right)\begin{bmatrix} 1\\ -3\end{bmatrix} \end{align*}\]

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

Now, notice that

\[\begin{align*} c\vec{v} &= c\left(c_1\begin{bmatrix} 1\\ -3\end{bmatrix}\right) = \left(c\cdot c_1\right)\begin{bmatrix} 1\\ -3\end{bmatrix} \end{align*}\]

But \(c\cdot c_1\) is just another scalar, which we can call \(c_2\), so \(c\vec{v}\in H~\checkmark\)

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

\(\vec{0} \in H\) \(\checkmark\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\) \(\checkmark\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\) \(\checkmark\)

Completed Example #1

Definition (Subspace Criteria): A subspace of \(\mathbb{R}^n\) is any set \(H\) in \(\mathbb{R}^n\) satisfying all of the following properties.

\(\vec{0} \in H\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\)

Example: Show that \(H = \text{span}\left(\left\{\left[\begin{array}{r} 1\\ -3\end{array}\right]\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

We’ll need to show that \(H\) satisfies the three requirements in the definition.

\(\vec{0} \in H\) \(\checkmark\)
If \(\vec{u}, \vec{v}\in H\), then \(\vec{u} + \vec{v}\in H\) \(\checkmark\)
If \(\vec{v}\in H\), then \(c\vec{v}\in H\) for any scalar \(c\) \(\checkmark\)

So \(H = \text{span}\left(\left\{\begin{bmatrix} 1\\ -3\end{bmatrix}\right\}\right)\) is a subspace of \(\mathbb{R}^2\).

Special Subspaces (Column Space)

Definition (Column Space): The column space corresponding to the matrix \(A\), denoted by \(\text{col}\left(A\right)\) is the set of all linear combinations of the columns of \(A\). That is, \(\text{col}\left(A\right) = \text{span}\left(\left\{\vec{a_1}, \vec{a_2}, \cdots, \vec{a_n}\right\}\right)\) where \(\vec{a_i}\) is the \(i^{th}\) column of the matrix \(A\).

Theorem (Column Space is a Subspace): If \(A\) is an \(m\times n\) matrix, then \(\text{col}\left(A\right)\) is a subspace of \(\mathbb{R}^m\).

Theorem (Basis for \(\text{col}\left(A\right)\)): The pivot columns of \(A\) form a basis for \(\text{col}\left(A\right)\).

An Important Note: In the Theorem listed above, it is important that we use pivot columns of the original matrix \(A\) as a basis for its column space. Often times the pivot columns of a row reduced version of \(A\) will not span \(\text{col}\left(A\right)\).

Completed Example #2

Example (Basis for Column Space): Find a basis for the column space of the matrix \(A = \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right]\).

We’ll need to identify the pivot columns in the matrix \(A\).

\[\begin{align*} \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right] \end{align*}\]

Completed Example #2

Example (Basis for Column Space): Find a basis for the column space of the matrix \(A = \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right]\).

We’ll need to identify the pivot columns in the matrix \(A\).

Completed Example #2

Example (Basis for Column Space): Find a basis for the column space of the matrix \(A = \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right]\).

We’ll need to identify the pivot columns in the matrix \(A\).

\[\begin{align*} \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right] \substack{R_2 \leftarrow R_2 + R_1\\ \longrightarrow} \left[\begin{array}{rrr} 1 & 3 & -2\\ 0 & 4 & 3\\ 0 & 4 & 3\end{array}\right]\\ \substack{R_3 \leftarrow R_3 + (-1R_2)\\ \longrightarrow} \left[\begin{array}{rrr} 1 & 3 & -2\\ 0 & 4 & 3\\ 0 & 0 & 0\end{array}\right] \end{align*}\]

Completed Example #2

Example (Basis for Column Space): Find a basis for the column space of the matrix \(A = \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right]\).

We’ll need to identify the pivot columns in the matrix \(A\).

\[\begin{align*} \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right] \substack{R_2 \leftarrow R_2 + R_1\\ \longrightarrow} \left[\begin{array}{rrr} 1 & 3 & -2\\ 0 & 4 & 3\\ 0 & 4 & 3\end{array}\right]\\ \substack{R_3 \leftarrow R_3 + (-1R_2)\\ \longrightarrow} \left[\begin{array}{rrr} \boxed{~1~} & 3 & -2\\ 0 & \boxed{~4~} & 3\\ 0 & 0 & 0\end{array}\right] \end{align*}\]

The first two columns of \(A\) are pivot columns.

Completed Example #2

Example (Basis for Column Space): Find a basis for the column space of the matrix \(A = \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right]\).

We’ll need to identify the pivot columns in the matrix \(A\).

\[\begin{align*} \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right] \substack{R_2 \leftarrow R_2 + R_1\\ \longrightarrow} \left[\begin{array}{rrr} 1 & 3 & -2\\ 0 & 4 & 3\\ 0 & 4 & 3\end{array}\right]\\ \substack{R_3 \leftarrow R_3 + (-1R_2)\\ \longrightarrow} \left[\begin{array}{rrr} \boxed{~1~} & 3 & -2\\ 0 & \boxed{~4~} & 3\\ 0 & 0 & 0\end{array}\right] \end{align*}\]

The first two columns of \(A\) are pivot columns.

A basis for \(\text{Col}\left(A\right)\) is

Completed Example #2

Example (Basis for Column Space): Find a basis for the column space of the matrix \(A = \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right]\).

We’ll need to identify the pivot columns in the matrix \(A\).

\[\begin{align*} \left[\begin{array}{rrr} 1 & 3 & -2\\ -1 & 1 & 5\\ 0 & 4 & 3\end{array}\right] \substack{R_2 \leftarrow R_2 + R_1\\ \longrightarrow} \left[\begin{array}{rrr} 1 & 3 & -2\\ 0 & 4 & 3\\ 0 & 4 & 3\end{array}\right]\\ \substack{R_3 \leftarrow R_3 + (-1R_2)\\ \longrightarrow} \left[\begin{array}{rrr} \boxed{~1~} & 3 & -2\\ 0 & \boxed{~4~} & 3\\ 0 & 0 & 0\end{array}\right] \end{align*}\]

The first two columns of \(A\) are pivot columns.

A basis for \(\text{Col}\left(A\right)\) is

\[\mathscr{B}_{\text{Col}} = \left\{\begin{bmatrix} 1\\ -1\\ 0\end{bmatrix}, \begin{bmatrix} 3\\ 1\\ 4\end{bmatrix}\right\}\]

Special Subspaces (Null Space)

Definition (Null Space): The null space of a matrix \(A\) is denoted by \(\text{Nul}\left(A\right)\) and is the set of all solutions to the homogeneous equation \(A\vec{x} = \vec{0}\).

Theorem (Null Space is a Subspace): For any \(m\times n\) matrix \(A\), \(\text{Nul}\left(A\right)\) is a subspace of \(\mathbb{R}^n\).

Completed Example #3

Example (Basis for Null Space): Find a basis for the null space of the matrix \(A = \left[\begin{array}{rrr} 1 & 2 & 0\\ 0 & 1 & 1\end{array}\right]\).

We’ll start by solving the homogeneous equation \(A\vec{x} = \vec{0}\).

\[\begin{align*} \left[\begin{array}{rrr|r} 1 & 2 & 0 & 0\\ 0 & 1 & 1 & 0\end{array}\right] \substack{R_1\leftarrow R_1 + (-2R2)\\ \longrightarrow} \left[\begin{array}{rrr|r} 1 & 0 & -2 & 0\\ 0 & 1 & 1 & 0\end{array}\right] \end{align*}\]

Notice that \(x_3\) is a free variable +The solution vector is then \(\vec{x} = \left[\begin{array}{r} 2x_3\\ -x_3\\ x_3\end{array}\right]\), which we can write in parametric vector form as \(\vec{x} = x_3\left[\begin{array}{r} 2\\ -1\\ 1\end{array}\right]\).

Completed Example #3

Example (Basis for Null Space): Find a basis for the null space of the matrix \(A = \left[\begin{array}{rrr} 1 & 2 & 0\\ 0 & 1 & 1\end{array}\right]\).

Since \(\vec{x} = x_3\left[\begin{array}{r} 2\\ -1\\ 1\end{array}\right]\)…

This means that any scalar multiple of \(\left[\begin{array}{r} 2\\ -1\\ 1\end{array}\right]\) is in \(\text{Nul}\left(A\right)\).
That is, a basis for \(\text{Nul}\left(A\right)\) is

\[\mathscr{B}_{\text{Nul}\left(A\right)} = \left\{\left[\begin{array}{r} 2\\ -1\\ 1\end{array}\right]\right\}\]

Dimension, Rank, Null Space, and Column Space

We’ll close by highlighting a few important observations about the ideas and objects we’ve introduced in this notebook.

The rank of a matrix \(A\) is the number of pivot positions in \(A\).
\(\dim\left(\text{Col}\left(A\right)\right) = \text{rank}\left(A\right)\)
Given an \(n\times n\) matrix \(A\), we have \(\dim\left(\text{Col}\left(A\right)\right) + \dim\left(\text{Null}\left(A\right)\right) = n\)

Examples to Try (1 of 4)

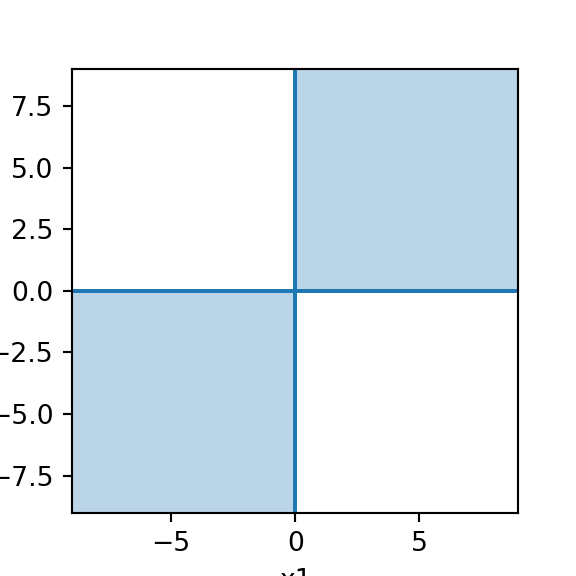
Example 1: Consider the plot on the right with solid (closed) boundary regions and assume that the shaded region extends infinitely. Determine whether the set corresponding to the shaded region (including its boundaries) is a subspace of \(\mathbb{R}^2\).

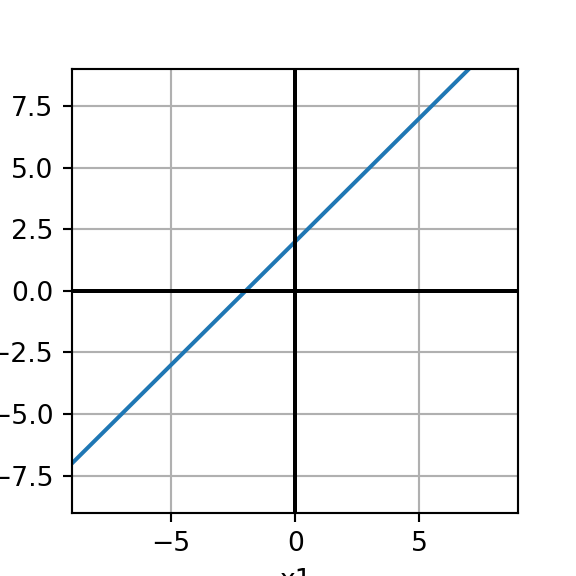
Example 2: Consider the plot to the left in which the blue line is the set \(H\). Assume that \(H\) extends infinitely in both directions. Determine whether or not \(H\) is a subspace of \(\mathbb{R}^2\).

Examples to Try (2 of 4)

Example 3: Consider the plot to the right in which the blue line is the set \(H\). Assume that \(H\) extends infinitely in both directions. Determine whether or not \(H\) is a subspace of \(\mathbb{R}^2\).

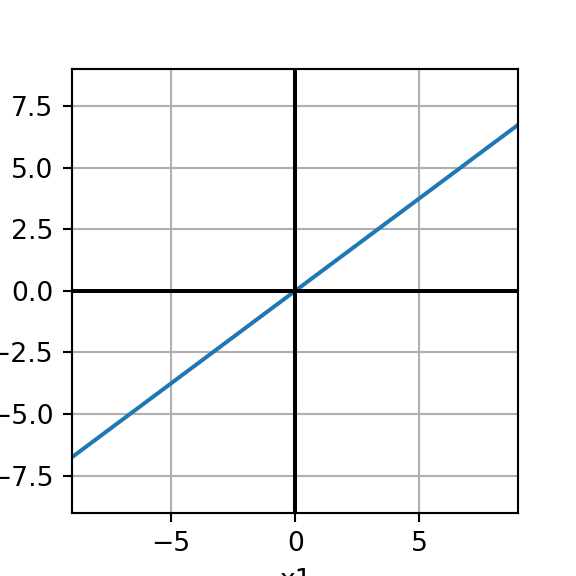
Example 4: Show that the null space of any \(3\times 4\) matrix \(A\) is a subspace of \(\mathbb{R}^n\) using the subspace criteria.

Examples to Try (3 of 4)

Example 5: Consider \(\vec{v_1} = \left[\begin{array}{r} 1\\ -3\\ 2\\ 3\end{array}\right]\), \(\vec{v_2} = \left[\begin{array}{r} 4\\ -4\\ 5\\ 7\end{array}\right]\), and \(\vec{v_3} = \left[\begin{array}{r} 5\\ -3\\ 6\\ 5\end{array}\right]\). Determine whether \(\vec{u} = \left[\begin{array}{r} -1\\ -7\\ -1\\ 2\end{array}\right]\) is in \(\text{span}\left(\left\{\vec{v_1}, \vec{v_2}, \vec{v_3}\right\}\right)\).

Example 6: Consider \(A = \left[\begin{array}{rrr} 1 & 2 & -8\\ 0 & -3 & 1\\ -1 & 1 & -1\end{array}\right]\). Determine whether \(\left[\begin{array}{r} 2\\ 3\\ 1\end{array}\right]\) is in \(\text{Nul}\left(A\right)\).

Examples to Try (4 of 4)

Example 7: The matrix \(A = \left[\begin{array}{rrrrr} 1 & 4 & 8 & -3 & -7\\ -1 & 2 & 7 & 3 & 4\\ -2 & 2 & 9 & 5 & 5\\ 3 & 6 & 9 & -5 & -2\end{array}\right]\) is row-equivalent the the echelon form matrix \(\left[\begin{array}{rrrrr} 1 & 4 & 8 & 0 & 5\\ 0 & 2 & 5 & 0 & -1\\ 0 & 0 & 0 & 1 & 4\\ 0 & 0 & 0 & 0 & 0\end{array}\right]\). Find a basis for \(\text{Col}\left(A\right)\) and a basis for \(\text{Nul}\left(A\right)\).

Example 8: Let \(A = \left[\begin{array}{rrr} 1 & 2 & 3\\ 2 & -1 & 1\\ 1 & 1 & 2\end{array}\right]\). Determine a basis for \(\text{Col}\left(A\right)\) and a basis for \(\text{Nul}\left(A\right)\).

Homework

\[\Huge{\text{Start Homework 11}}\] \[\Huge{\text{on MyOpenMath}}\]

Next Time…

\(\Huge{\text{Introduction to}}\)

\(\Huge{\text{Eigenvectors and Eigenvalues}}\)