MAT 350: Introduction and What to Expect

Dr. Gilbert

August 19, 2025

What Are We Here For?

\[\left\{\begin{array}{lcl} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\]

What Are We Here For?

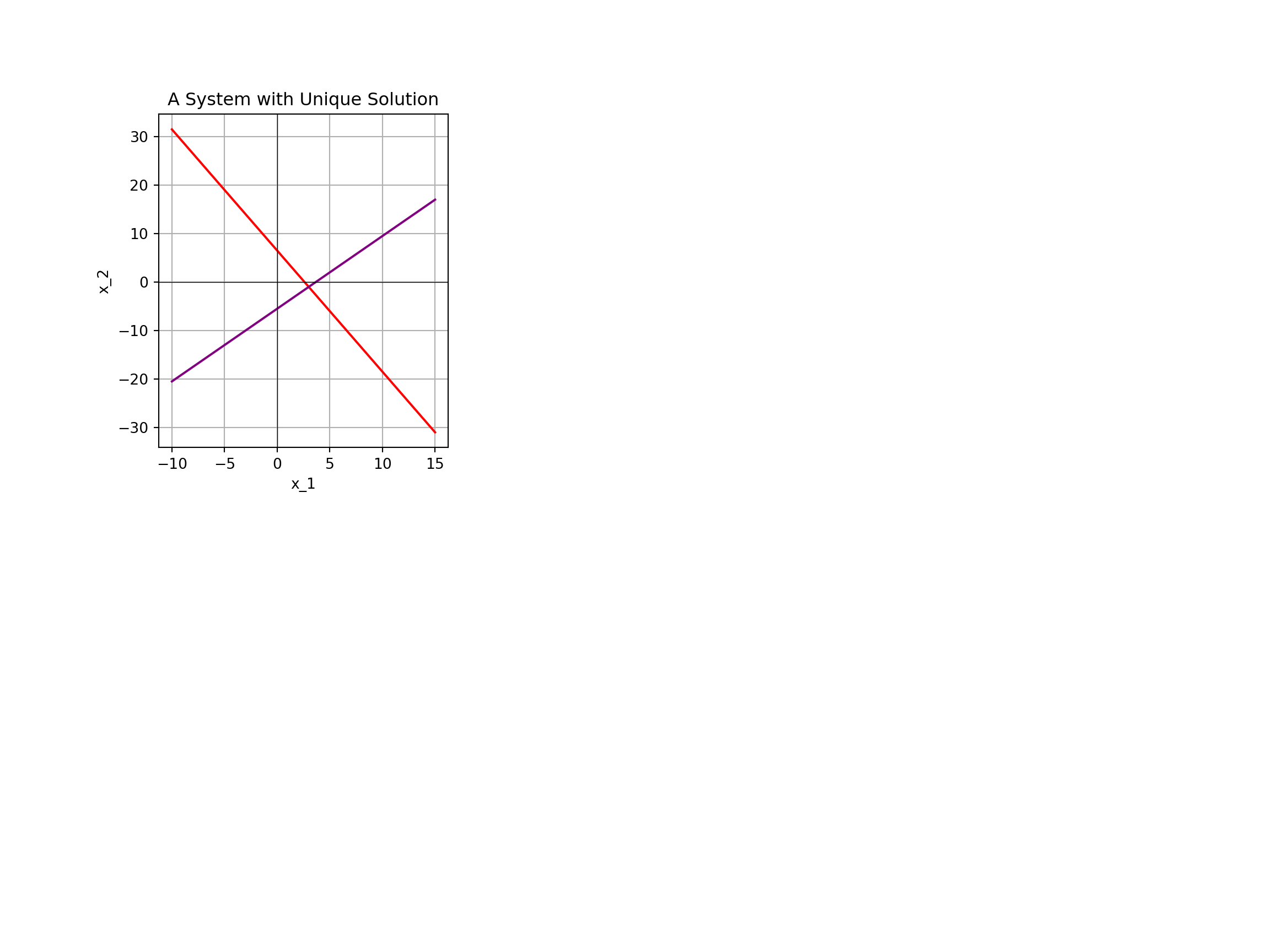
\[\left\{\begin{array}{lcl} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\]

What Are We Here For?

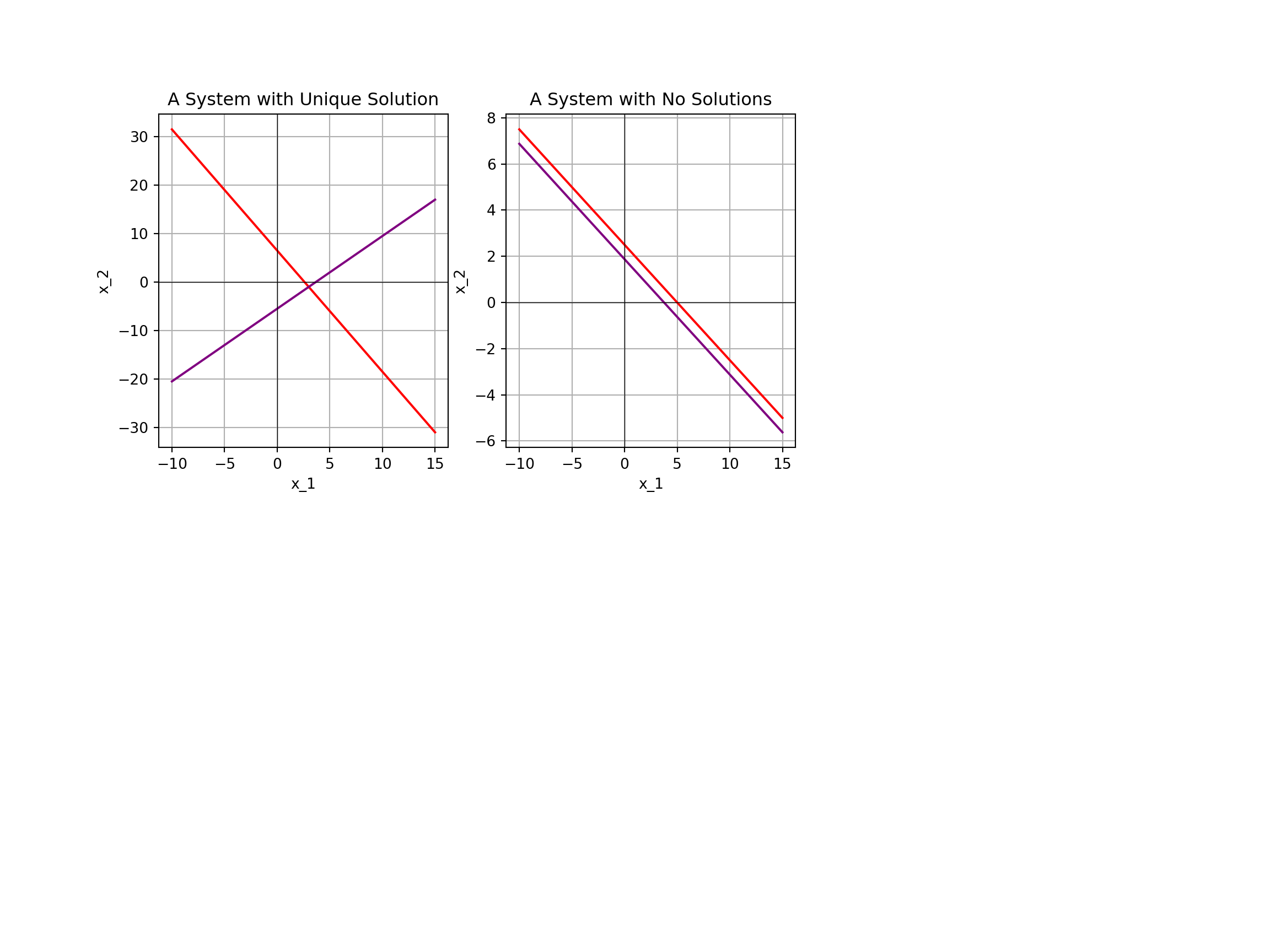
\[\left\{\begin{array}{lcl} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\]

\[\left\{\begin{array}{lcl} 2x_1 + 4x_2 & = & 10\\ 4x_1 + 8x_2 & = & 15\end{array}\right.\]

What Are We Here For?

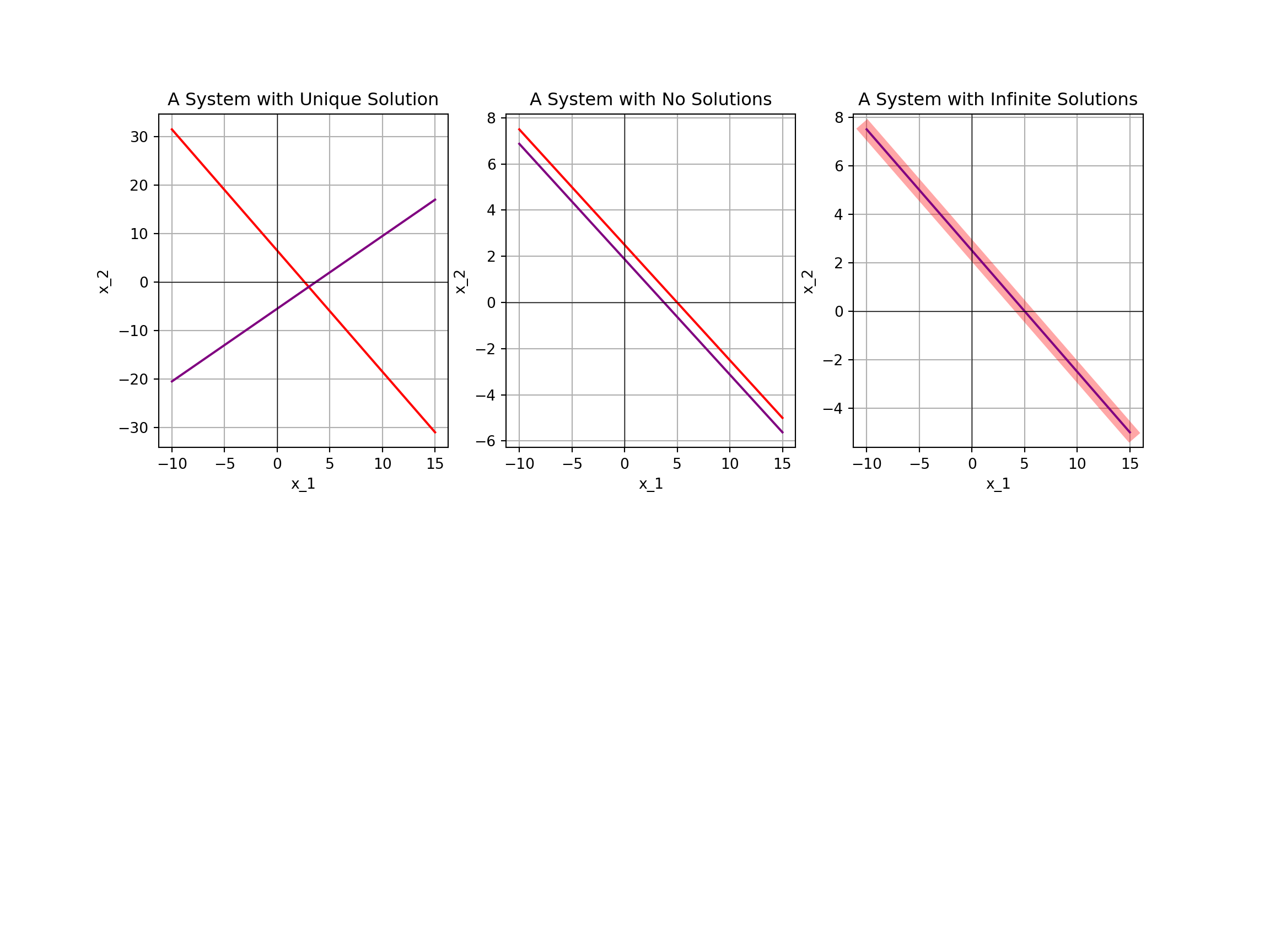
\[\left\{\begin{array}{lcl} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\]

\[\left\{\begin{array}{lcl} 2x_1 + 4x_2 & = & 10\\ 4x_1 + 8x_2 & = & 15\end{array}\right.\]

\[\left\{\begin{array}{lcl} 2x_1 + 4x_2 & = & 10\\ -4x_1 - 8x_2 & = & -20\end{array}\right.\]

What Are We Here For?

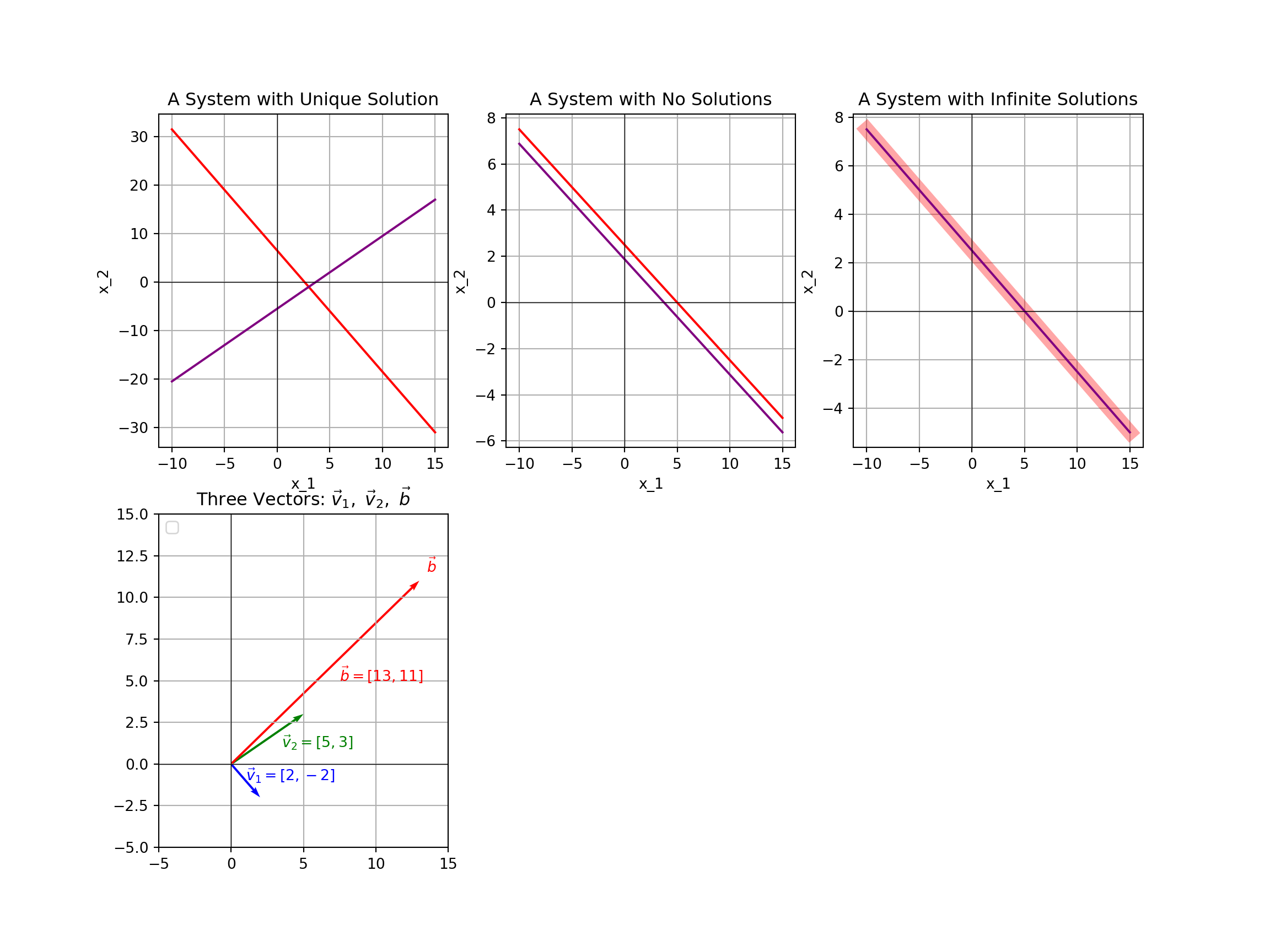
\[\left\{\begin{array}{lcl} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\]

\[\left\{\begin{array}{lcl} 2x_1 + 4x_2 & = & 10\\ 4x_1 + 8x_2 & = & 15\end{array}\right.\]

\[\left\{\begin{array}{lcl} 2x_1 + 4x_2 & = & 10\\ -4x_1 - 8x_2 & = & -20\end{array}\right.\]

What Are We Here For?

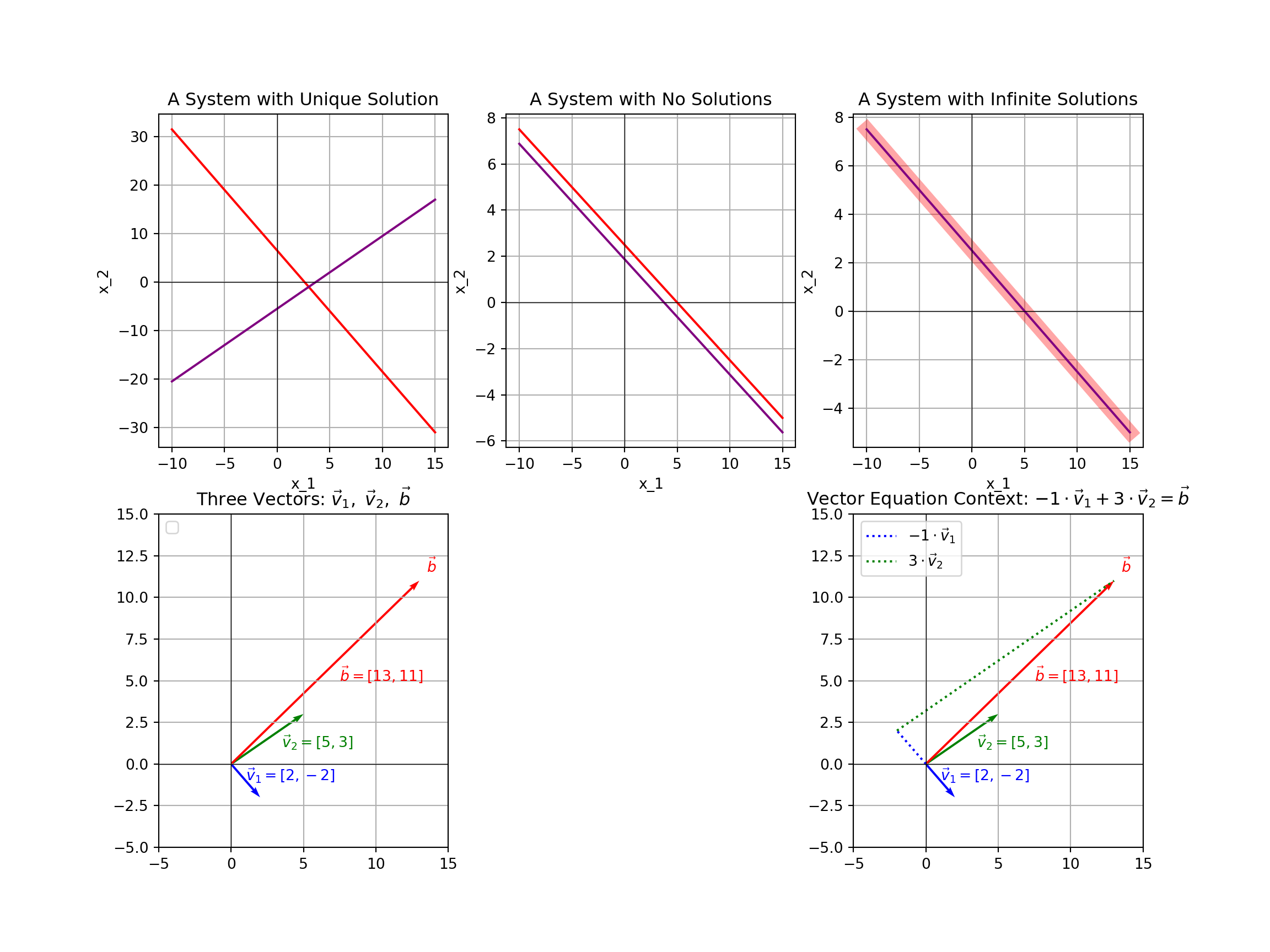
\[\left\{\begin{array}{lcl} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\]

\[\left\{\begin{array}{lcl} 2x_1 + 4x_2 & = & 10\\ 4x_1 + 8x_2 & = & 15\end{array}\right.\]

\[\left\{\begin{array}{lcl} 2x_1 + 4x_2 & = & 10\\ -4x_1 - 8x_2 & = & -20\end{array}\right.\]

\[c_1\begin{bmatrix} 2\\ -2\end{bmatrix} + c_2\begin{bmatrix} 5\\ 3\end{bmatrix} = \begin{bmatrix} 13\\ 11\end{bmatrix}\]

What Are We Here For?

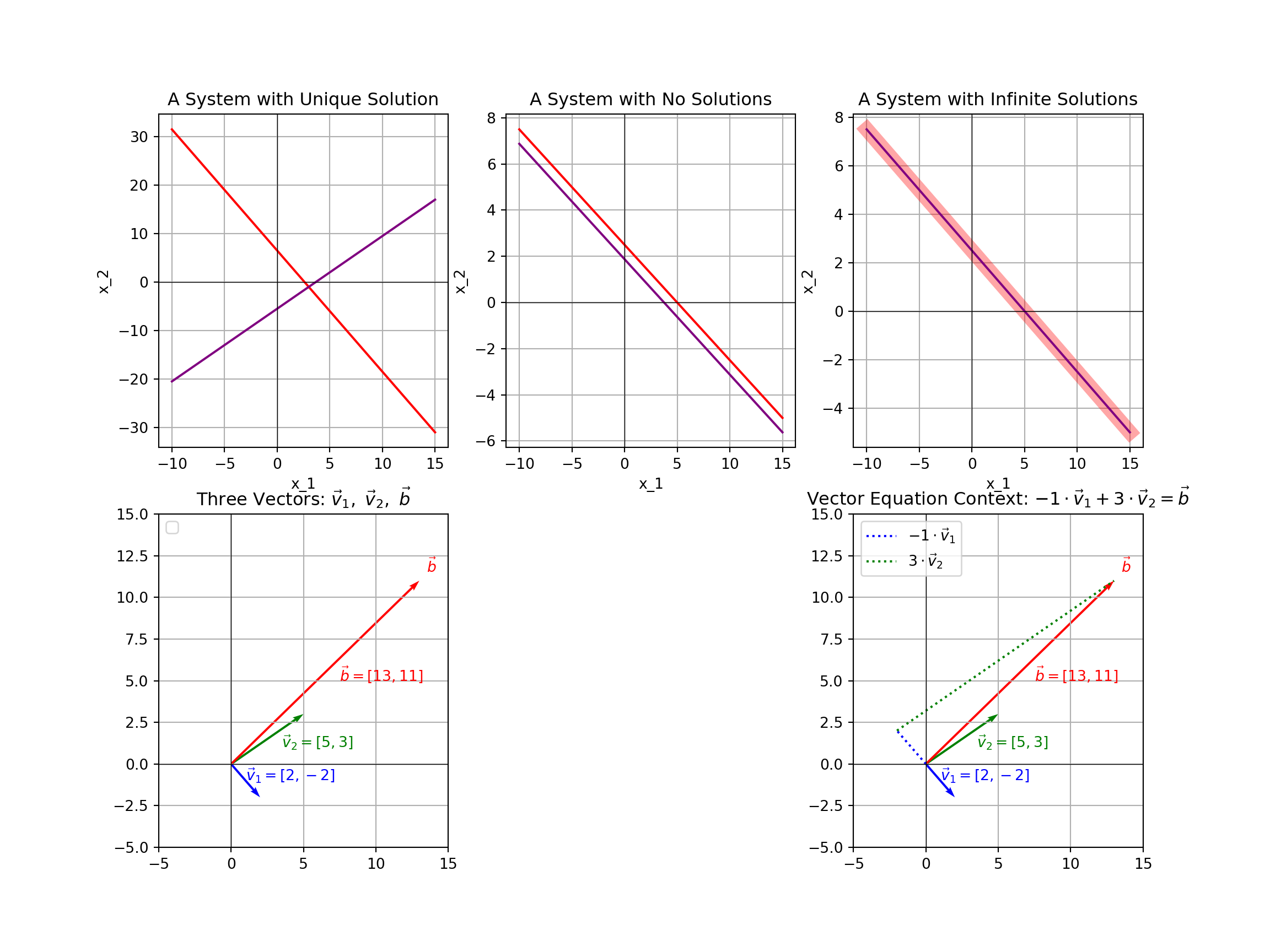
\[\left\{\begin{array}{lcl} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\]

\[\left\{\begin{array}{lcl} 2x_1 + 4x_2 & = & 10\\ 4x_1 + 8x_2 & = & 15\end{array}\right.\]

\[\left\{\begin{array}{lcl} 2x_1 + 4x_2 & = & 10\\ -4x_1 - 8x_2 & = & -20\end{array}\right.\]

\[c_1\begin{bmatrix} 2\\ -2\end{bmatrix} + c_2\begin{bmatrix} 5\\ 3\end{bmatrix} = \begin{bmatrix} 13\\ 11\end{bmatrix}\]

\[\text{...and more...}\]

Syllabus

Major Highlights from the Syllabus: I’ll ask you to read the syllabus, but the most important items are on the following slides.

Instructor and Office Hours

  • Instructor: Dr. Adam Gilbert

    • e-mail address: a.gilbert1@snhu.edu

    • Office: Robert Frost Hall, Room 311

    • Office Hours (please visit!):

      • Wednesdays 9:00am - 10:30am
      • Thursdays 9:00am - 10:30am
      • Fridays 1:00pm - 3:00pm

Required Resources

First and foremost…everything is free!

  • Main Textbook: We are following Understanding Linear Algebra by David Austin, but myself and Dr. Spaulding have adapted a custom Python version

  • Python via Google Colab or a local Python installation is recommended but not required

  • Online Homework at MyOpenMath is a required component of this course

    • The CourseID and Enrollment Key are available in the Welcome! announcement on BrightSpace.

Grading Scheme

Grade Item Value
Homework (~12) 25%
Row-Reduction Gateway Exam 15%
Exams (2) 40%
Final Exam 20%

Explanations of Grade Items

  • Homework: Practicing is critical to your success in linear algebra. You’ll get unlimited attempts (unpenalized) at all problems on each assignment, and you’ll be graded 50% on completion and 50% on correctness.

    • Late Passes: You get three free (no penalty) late passes to open up assignments again until the end of the semester. No additional late passes will be provided though.

  • Row-Reduction Gateway: Row-reduction is a procedure that we’ll utilize over and over again in linear algebra. This gateway can be taken many times and is an “all or nothing” component of the grading scheme.

  • Exams: We’ll have two exams during the semester – each will include a group exam (20%) and an individual exam (80%), where the group exam only counts if your group score exceeds your individual score.

  • Final Exam: The final exam will occur in two parts during the last week of the semester. The first part is required and the second part is optional. The final exam can be used to improve earlier exam grades.

Brightspace

  • Announcements
  • Gradebook
  • Go to the webpage for everything else

Course Webpage

I’ve built a webpage to organize our course content.

  • Syllabus

  • Tentative timeline

    • Links to full notes (in Jupyter/Colab notebook format)
    • Links to the discussion slide versions of those notes
    • Assignment reminders
    • Optional, but recommended, 3Blue1Brown high-level overview videos

What’s Class Like?

  • Some lecture is going to be necessary here
  • I have complete sets of notes for you and will attempt to keep up with building slides if you want them
  • I hope to spend significant class time on collaborative discussion and problem-solving

A Note on Approach to Class

  • I’m open to change in all of my courses.
  • If the structure isn’t working for you, let’s chat and see what changes we can make to improve your experience.
  • If you don’t want to tell me in person, leave an anonymous note under my office door.

My goal in this course is for all of you to learn as much about linear algebra and its applications as possible – we can’t achieve that if you don’t feel like you are benefiting from our class meetings.

A Road Map to Our Semester

We’ll be discussing a lot of material in MAT 350. Here is a very generic road map of what we will discuss. Starting now.

A Linear Algebra Road Map

  • Motivation for Linear Algebra (Today)

  • Foundations

    • Vectors and Arithmetic
    • Matrices and Arithmetic

  • Linear Systems

    • Solving Systems
    • Pivots
    • Solution Spaces

  • Vector Equations

    • Linear Combinations
    • Linear Independence
    • Spanning Sets
    • Bases

  • Matrix Transformations

  • Matrix Equations

    • Invertibility
    • Determinants
    • More with Bases and Subspaces

  • Eigenvectors and Eigenvalues

  • Diagonalization

  • Discrete Dynamical Systems

  • Markov Chains and Google Page Rank

Conventions and Definitions Before We Continue

  1. Convention for Writing linear Equations: We’ll write all of our linear equations to include all variable terms on the left side of the equation and pushing the constant term to the right. That is, we’ll write \(x_1 + 8x_2 = -7\) rather than \(x_1 = -8x_2 -7\)

    • Why? Consistency. We can write any linear equation this way, regardless of the number of variables included or whether the line is vertical or horizontal.

  2. Terminology for Linear Equations: Given a linear equation of the form \(a_1x_1 + a_2x_2 + \cdots + a_nx_n = b\), we say that

    • \(a_1, a_2,\cdots, a_n\) are the coefficients, sometimes called scalars or weights in different contexts.
    • \(x_1, x_2,\cdots, x_n\) are the variables (or unknowns).
    • the constant \(b\) is sometimes referred to as the constant term, intercept, or right-hand side.

Conventions and Definitions Before We Continue (Cont’d)

  1. Systems of Linear Equations (or linear systems) are a collection of linear equations written with a common set of unknowns and designed to be solved simultaneously.

  2. Solution for Linear Systems (or solution) is a collection of scalars (numbers) \(x_1 = s_1, x_2 = s_2, \cdots, x_n = s_n\) that satisfy all of the equations in the system simultaneously.

  3. Solution Space (or solution set) for a linear system is the collection of all solutions to a given linear system.

    • Remember that for any give system we may have 0, 1, or infinitely many solutions. That is, the solution space is either empty, contains a single element, or contains infinitely many elements.

Solving Our First System

Example 1: Solve the linear system \(\left\{\begin{array}{rcr} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\)

  1. Add the first and second equations together to get a new equation \(0x_1 + 8x_2 = 24\), or more simply \(8x_2 = 24\).
  2. Solve this new equation for \(x_2\) to find that \(x_2 = 3\).
  3. Plug your newly discovered value of \(x_2\) into either equation to eliminate one of the unknowns, resulting in a single equation with one unknown that can be solved for.

\[\begin{align} 2x_1 + 5x_2 &= 13 \end{align}\]

Solving Our First System

Example 1: Solve the linear system \(\left\{\begin{array}{rcr} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\)

  1. Add the first and second equations together to get a new equation \(0x_1 + 8x_2 = 24\), or more simply \(8x_2 = 24\).
  2. Solve this new equation for \(x_2\) to find that \(x_2 = 3\).
  3. Plug your newly discovered value of \(x_2\) into either equation to eliminate one of the unknowns, resulting in a single equation with one unknown that can be solved for.

\[\begin{align} 2x_1 + 5x_2 &= 13\\ \implies 2x_1 + 5\left(3\right) &= 13 \end{align}\]

Solving Our First System

Example 1: Solve the linear system \(\left\{\begin{array}{rcr} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\)

  1. Add the first and second equations together to get a new equation \(0x_1 + 8x_2 = 24\), or more simply \(8x_2 = 24\).
  2. Solve this new equation for \(x_2\) to find that \(x_2 = 3\).
  3. Plug your newly discovered value of \(x_2\) into either equation to eliminate one of the unknowns, resulting in a single equation with one unknown that can be solved for.

\[\begin{align} 2x_1 + 5x_2 &= 13\\ \implies 2x_1 + 5\left(3\right) &= 13\\ \implies 2x_1 + 15 &= 13 \end{align}\]

Solving Our First System

Example 1: Solve the linear system \(\left\{\begin{array}{rcr} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\)

  1. Add the first and second equations together to get a new equation \(0x_1 + 8x_2 = 24\), or more simply \(8x_2 = 24\).
  2. Solve this new equation for \(x_2\) to find that \(x_2 = 3\).
  3. Plug your newly discovered value of \(x_2\) into either equation to eliminate one of the unknowns, resulting in a single equation with one unknown that can be solved for.

\[\begin{align} 2x_1 + 5x_2 &= 13\\ \implies 2x_1 + 5\left(3\right) &= 13\\ \implies 2x_1 + 15 &= 13\\ \implies 2x_1 &= -2 \end{align}\]

Solving Our First System

Example 1: Solve the linear system \(\left\{\begin{array}{rcr} 2x_1 + 5x_2 & = & 13\\ -2x_1 + 3x_2 & = & 11\end{array}\right.\)

  1. Add the first and second equations together to get a new equation \(0x_1 + 8x_2 = 24\), or more simply \(8x_2 = 24\).
  2. Solve this new equation for \(x_2\) to find that \(x_2 = 3\).
  3. Plug your newly discovered value of \(x_2\) into either equation to eliminate one of the unknowns, resulting in a single equation with one unknown that can be solved for.

\[\begin{align} 2x_1 + 5x_2 &= 13\\ \implies 2x_1 + 5\left(3\right) &= 13\\ \implies 2x_1 + 15 &= 13\\ \implies 2x_1 &= -2\\ \implies x_1 &= -1 \end{align}\]

  1. Identify and describe the solutions we’ve discovered. From the work above, we see that a solution to the system exists and that solution is \(\boxed{~\displaystyle{x_1 = -1} \text{ and } \displaystyle{x_2 = 3}~}\).

Solving Our First Vector Equation

Example 2: Solve the vector equation \(c_1\begin{bmatrix} 2\\ -2\end{bmatrix} + c_2\begin{bmatrix} 5\\ 3\end{bmatrix} = \begin{bmatrix} 13\\ 11\end{bmatrix}\)

  1. Notice that the vector equation is equivalent to \(\begin{bmatrix} 2c_1\\ -2c_1\end{bmatrix} + \begin{bmatrix} 5c_2\\ 3c_2\end{bmatrix} = \begin{bmatrix} 13\\ 11\end{bmatrix}\)
  2. This is further equivalent to \(\begin{bmatrix} 2c_1 + 5c_2\\ -2c_1 + 3c_2\end{bmatrix} = \begin{bmatrix} 13\\ 11\end{bmatrix}\)
  3. This is equivalent to our system from Example 1, so the solution is \(\boxed{~\displaystyle{c_1 = -1 \text{ and } c_2 = 3}~}\)

Benefits to Different Contexts

The linear system from Example 1 is a question about the point of intersection between two lines, while the vector equation from Example 2 is a question about linear combinations and spans (which we’ll see later in our course)

Put more simply, the vector equation from Example 2 asks whether it is possible to begin from \(\begin{bmatrix} 0\\ 0\end{bmatrix}\) (the origin) and walk only in the directions of \(\begin{bmatrix} 2\\ -2\end{bmatrix}\) and \(\begin{bmatrix} 5\\ 3\end{bmatrix}\) and arrive at the location \(\begin{bmatrix} 13\\ 11\end{bmatrix}\)

Benefits to Different Contexts

The linear system from Example 1 is a question about the point of intersection between two lines, while the vector equation from Example 2 is a question about linear combinations and spans (which we’ll see later in our course)

Put more simply, the vector equation from Example 2 asks whether it is possible to begin from \(\begin{bmatrix} 0\\ 0\end{bmatrix}\) (the origin) and walk only in the directions of \(\begin{bmatrix} 2\\ -2\end{bmatrix}\) and \(\begin{bmatrix} 5\\ 3\end{bmatrix}\) and arrive at the location \(\begin{bmatrix} 13\\ 11\end{bmatrix}\)

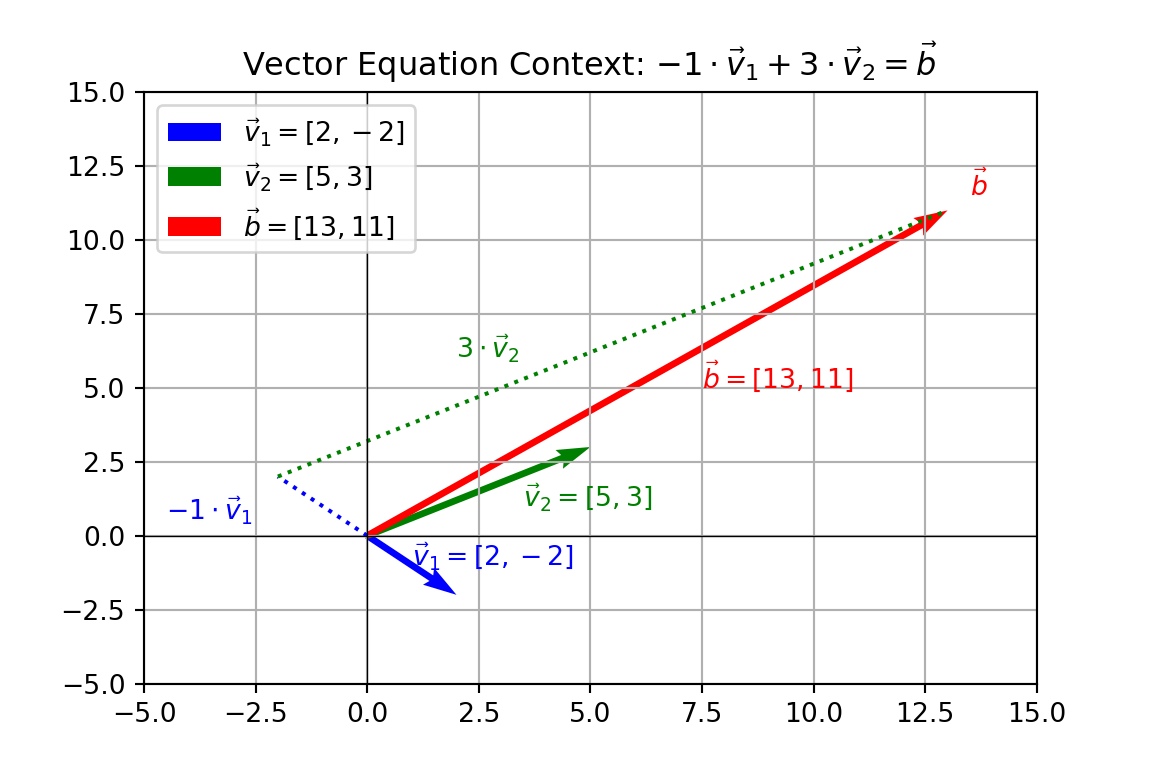
Benefits to Different Contexts (Cont’d)

The vector equation context becomes quite useful because, while it is hard to visualize the meaning of a solution set to the system

\[\left\{\begin{array}{lcl} 5x_1 + 4x_2 - 2x_3 + x_4 & = & 8\\ -x_1 + x_2 - x_3 + x_4 & = & 5\\ -4x_1 + 3x_2 + 8x_3 - 4x_4 & = & -7\\ 2x_1 + 3x_2 - x_3 - x_4 & = & -12\end{array}\right.\]

It is much easier to grasp the meaning of the solution set to the vector equation

\[c_1\begin{bmatrix} 5\\ -1\\ -4\\ 2\end{bmatrix} + c_2\begin{bmatrix} 4\\ 1\\ 3\\ 3\end{bmatrix} + c_3\begin{bmatrix} -2\\ -1\\ 8\\ -1\end{bmatrix} + c_4\begin{bmatrix} 1\\ 1\\ -4\\ -1\end{bmatrix} = \begin{bmatrix} 8\\ 5\\ -7\\ -12\end{bmatrix}\]

Benefits to Different Contexts (Cont’d)

It is much easier to grasp the meaning of the solution set to the vector equation

\[c_1\begin{bmatrix} 5\\ -1\\ -4\\ 2\end{bmatrix} + c_2\begin{bmatrix} 4\\ 1\\ 3\\ 3\end{bmatrix} + c_3\begin{bmatrix} -2\\ -1\\ 8\\ -1\end{bmatrix} + c_4\begin{bmatrix} 1\\ 1\\ -4\\ -1\end{bmatrix} = \begin{bmatrix} 8\\ 5\\ -7\\ -12\end{bmatrix}\]

We have four directional vectors that we can walk in – and we wonder whether we can arrive at a particular point in space.

Homework (Part I)

  • Complete the Week One assignment in BrightSpace

  • Complete Homework 0 on MyOpenMath

    • See Welcome Announcement on BrightSpace for Course ID and Enrollment Key

Homework (Part II)

Stop by my office (Robert Frost 311), say hi and let’s briefly chat about the following:

  • Why are you taking this course?
  • What do you hope to get out of it?
  • What can I do to make it likely that you have a good experience in this course?

Next Time…




\(\Huge{\text{Vectors and Arithmetic}}\)




Optional: Watch 3Blue1Brown: Vectors to prepare