MAT 350: Spans of Collections of Vectors

Warm-Up Problems

Complete the following warm-up problems to re-familiarize yourself with concepts we’ll be leveraging today.

Compute the linear combination \(c_1\vec{v_1} + c_2\vec{v_2} + c_3\vec{v_3}\) where \(\vec{v_1} = \begin{bmatrix} -3\\ 1\\ 5\end{bmatrix},~\vec{v_2} = \begin{bmatrix} 1\\ 1\\ -1\end{bmatrix}\), and \(\vec{v_3} = \begin{bmatrix} 0\\ 0\\ 2\end{bmatrix}\) with \(c_1 = -1\), \(c_2 =-4\), and \(c_3 = 5\).
Determine whether the vector \(\begin{bmatrix} -4\\ 3\end{bmatrix}\) is a linear combination of the vectors \(\vec{v_1} = \begin{bmatrix} 2\\ 8\end{bmatrix}\) and \(\vec{v_2} = \begin{bmatrix} -1\\ 1\end{bmatrix}\).
What must be true about all vectors which are linear combinations of the vectors \(\vec{v_1} = \begin{bmatrix} -3\\ -1\\ 0\end{bmatrix}\) and \(\vec{v_2} = \begin{bmatrix} 0\\ 1\\ 0\end{bmatrix}\)?
Solve the matrix equation \(A\vec{x} = \vec{0}\), where \(A = \begin{bmatrix} 1 & 2 & 0 & 1 & -3\\ 0 & 0 & 1 & -4 & 6\\ 1 & 2 & 1 & -3 & 3 \end{bmatrix}\). Write the solution in parametric vector form and describe the solution space.

Reminders and Today’s Goal

A linear combination of vectors \(\vec{v_1}, \vec{v_2}, \dots, \vec{v_k}\) is any vector that can be written as
\(\quad \vec{y} = c_1\vec{v_1} + c_2\vec{v_2} + \dots + c_k\vec{v_k}\)
where \(c_1, c_2, \dots, c_k\) are scalars.
Linear combinations let us “move” through space by scaling and adding given vectors.
Our set of available vectors determines which parts of \(\mathbb{R}^n\) we can reach.

Goals for Today: By the end of class, you should be able to:

Define the span of a collection of vectors.
Decide whether a given vector \(\vec{b}\) is in the span of a set of vectors.
Describe the geometry of the span in \(\mathbb{R}^n\) (point, line, plane, …).

Motivating the Span

We’ve spent our last two meetings focused on linear combinations of vectors.
Again, a vector \(\vec{y}\) can be written as a linear combination of the vectors \(\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_p}\) if there exist scalars \(c_1,~c_2,~\cdots,~c_p\) such that \(c_1\vec{v_1} + c_2\vec{v_2} + \cdots + c_p\vec{v_p} = \vec{y}\).

New Question: Given the collection of vectors \(\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_p}\), “what types of vectors can be written as linear combinations of the vectors in my collection?”

This is similar to what was asked in the third warm-up problem in this notebook.
That is the question we’ll focus on in this notebook.

Spans of Vectors

Definition (Span of a Collection of Vectors): Given some collection of vectors \(\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_p}\) from \(\mathbb{R}^n\), the set of all linear combinations of these vectors is called its span and is denoted by \(\text{span}\left(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_p}\right\}\right)\).

Example: Determine whether the vector \(\vec{b} = \left[\begin{array}{r} -15\\ -1\\ -7\end{array}\right]\) is in \(\text{span}\left(\left\{\left[\begin{array}{r} 1\\ 3\\ 1\end{array}\right], \left[\begin{array}{r} -3\\ 2\\ -1\end{array}\right]\right\}\right)\).

We are searching for \(c_1\) and \(c_2\) such that \(c_1\begin{bmatrix} 1\\ 3\\ 1\end{bmatrix} + c_2\begin{bmatrix} -3\\ 2\\ -1\end{bmatrix} = \begin{bmatrix} -15\\ -1\\ -7\end{bmatrix}\)
We construct an augmented matrix whose first two columns are the vectors whose span we are interested in, and whose augmented column is the vector \(\vec{b}\)

Spans of Vectors

Example: Determine whether the vector \(\vec{b} = \left[\begin{array}{r} -15\\ -1\\ -7\end{array}\right]\) is in \(\text{span}\left(\left\{\left[\begin{array}{r} 1\\ 3\\ 1\end{array}\right], \left[\begin{array}{r} -3\\ 2\\ -1\end{array}\right]\right\}\right)\).

We are searching for \(c_1\) and \(c_2\) such that \(c_1\begin{bmatrix} 1\\ 3\\ 1\end{bmatrix} + c_2\begin{bmatrix} -3\\ 2\\ -1\end{bmatrix} = \begin{bmatrix} -15\\ -1\\ -7\end{bmatrix}\)
We construct an augmented matrix whose first two columns are the vectors whose span we are interested in, and whose augmented column is the vector \(\vec{b}\)

import sympy as sp

A = sp.Matrix([[1.0, -3, -15], 
              [3, 2, -1], 
              [1, -1, -7]])
A.rref()

(Matrix([
[1, 0, -3.0],
[0, 1,  4.0],
[0, 0,    0]]), (0, 1))

Spans of Vectors

Example: Determine whether the vector \(\vec{b} = \left[\begin{array}{r} -15\\ -1\\ -7\end{array}\right]\) is in \(\text{span}\left(\left\{\left[\begin{array}{r} 1\\ 3\\ 1\end{array}\right], \left[\begin{array}{r} -3\\ 2\\ -1\end{array}\right]\right\}\right)\).

We are searching for \(c_1\) and \(c_2\) such that \(c_1\begin{bmatrix} 1\\ 3\\ 1\end{bmatrix} + c_2\begin{bmatrix} -3\\ 2\\ -1\end{bmatrix} = \begin{bmatrix} -15\\ -1\\ -7\end{bmatrix}\)
We construct an augmented matrix whose first two columns are the vectors whose span we are interested in, and whose augmented column is the vector \(\vec{b}\)

import sympy as sp

A = sp.Matrix([[1.0, -3, -15], 
              [3, 2, -1],
              [1, -1, -7]])
A.rref()

(Matrix([
[1, 0, -3.0],
[0, 1,  4.0],
[0, 0,    0]]), (0, 1))

So \(c_1 = -3\) and \(c_2 = 4\), and \(\begin{bmatrix} -15\\ -1\\ -7\end{bmatrix}\) is in \(\text{span}\left(\left\{\begin{bmatrix} 1\\ 3\\ 1\end{bmatrix}, \begin{bmatrix} -3\\ 2\\ -1\end{bmatrix}\right\}\right)~~_{\blacktriangledown}\)

Example to Try #1

Example: Is the vector \(\vec{b} = \left[\begin{array}{c}1\\ 5\\ 3\end{array}\right]\) in \(\text{span}\left(\left\{\left[\begin{array}{c} 1\\ 1\\ 0\end{array}\right], \left[\begin{array}{c} 0\\ 1\\ 1\end{array}\right]\right\}\right)\)?

Interesting Questions Around Spans

The question of what space a set of vectors span is quite an interesting one.

For example, do the vectors \(\vec{v_1} = \left[\begin{array}{c} 2\\ 3\end{array}\right]\) and \(\vec{v_2} = \left[\begin{array}{c}4\\ 6\end{array}\right]\) span all of \(\mathbb{R}^2\)?
This question amounts to asking which points in \(\mathbb{R}^2\) can be arrived at by taking scaled steps in the direction of \(\vec{v_1}\) and \(\vec{v_2}\).

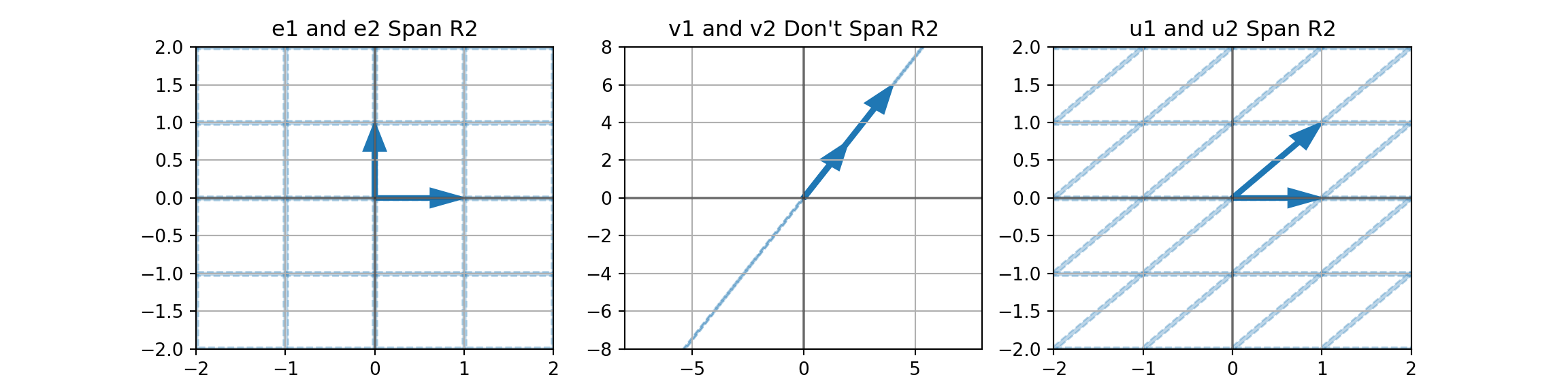
Check out this “applet”.

When do Vectors Span an Entire Space?

We’ve seen examples of pairs of vectors from \(\mathbb{R}^2\) that span \(\mathbb{R}^2\) and others that don’t.
- In the latter case, there were some vectors (locations in \(\mathbb{R}^2\) which could not be reached using steps only in the directions of the two vectors being investigated).
So, when do two vectors from \(\mathbb{R}^2\) actually span all of \(\mathbb{R}^2\)?
More generally, when does a collection of vectors from \(\mathbb{R}^m\) span all of \(\mathbb{R}^m\)?

When do Vectors Span and Entire Space?

Equivalent Statements: The following statements are equivalent.

The collection of vectors \(\left\{\vec{v_1}, \vec{v_2}, \cdots, \vec{v_p}\right\}\) spans \(\mathbb{R}^m\).
The vector equation \(x_1\vec{v_1} + x_2\vec{v_2} + \cdots + x_p\vec{v_p} = \vec{b}\) has a solution for every \(\vec{b} \in\mathbb{R}^m\).
The matrix equation \(\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_p}\end{bmatrix}\vec{x} = \vec{b}\) has a solution for every \(\vec{b}\in\mathbb{R}^m\).
The matrix \(\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_p}\end{bmatrix}\) has a pivot in every row, making it impossible for the augmented matrix \(\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_p} & | & \vec{b}\end{bmatrix}\) to have a pivot in its rightmost column.
The linear system \(\left\{\begin{array}{rcr} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n & = & b_1\\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n & = & b_2\\ & \vdots & \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n & = & b_n\end{array}\right.\) is consistent for all choices of \(b_1,~b_2,~\cdots,~b_n\).

When do Vectors Span an Entire Space? Example to Try #2

Example: Determine whether the collection of vectors \(\left\{\begin{bmatrix} 1\\ 0\\ -1\end{bmatrix}, \begin{bmatrix} 5\\ -2\\ 8\end{bmatrix}, \begin{bmatrix} 7\\ -2\\ 6\end{bmatrix}, \begin{bmatrix} 1\\ 1\\ -1\end{bmatrix}\right\}\) spans \(\mathbb{R}^3\)

Describing the Space Spanned

Even if a collection of vectors \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_p}\right\}\) does not span all of \(\mathbb{R}^m\), it is possible to describe the subset of \(\mathbb{R}^m\) that is spanned by the collection.
- Solve the matrix equation \(\begin{bmatrix} \vec{v_1} & \vec{v_2} & \cdots & \vec{v_p}\end{bmatrix} \vec{x} = \vec{b}\) for an arbitrary \(\vec{b}\in \mathbb{R}^m\). That is, we row-reduce the following augmented matrix

\[\left[\begin{array}{cccc|c} v_{11} & v_{12} & \cdots & v_{1p} & b_1\\ v_{12} & v_{22} & \cdots & v_{2p} & b_2\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ v_{1m} & v_{m2} & \cdots & v_{mp} & b_m\end{array}\right]\]

All vectors \(\vec{b}\) such that the right-most column is not a pivot column are in the span of the collection of vectors.
- Identifying the requirements for preventing the pivot will shed light on the vectors \(\vec{b}\in\mathbb{R}^m\) which are spanned by \(\left\{\vec{v_1},~\vec{v_2},~\cdots,~\vec{v_p}\right\}\)