Practice Inference: Two Examples
November 14, 2024
The Highlights
A completed example problem together
Another completed example problem together
Hypothesis Testing; what could go wrong?
- A short discussion on statistical errors, error types, and the likelihood of errors
Completed Example 1: Water Contamination
Scenario: Environmental scientists are studying water quality in a river system and want to estimate the proportion of water samples that exceed a specific contaminant threshold. They aim for a 99% confidence level and to capture the population parameter to within two percentage points of the true population proportion. These thresholds are necessary to ensure reliability of their findings, especially as the data could inform public health advisories. The results of a small, initial investigation indicate that the proportion is near 25%. How many sections of the river system should they collect water samples from?
- This scenario is asking us to compute a required sample size
- The population parameter is a proportion
- The sample size formula is \(\displaystyle{n\geq \left(\frac{z_{\alpha/2}}{M_E}\right)^2\cdot p\left(1 - p\right)}\)
- The critical value (\(z_{\alpha/2}\)) is 2.58
- The margin of error is 0.02
- Our best guess at the proportion is \(p \approx 0.25\) (note that using \(p \approx 0.50\) results in a “worst case” largest sample size requirement).
- \(\displaystyle{n\geq \left(\frac{2.58}{0.02}\right)^2\cdot 0.25\left(1 - 0.25\right) \approx 3120.188}\)
- The scientists should sample from 3121 randomly identified locations along the river system.
Completed Example 2: Blood Pressure Medication
Scenario: A pharmaceutical company claims that a new medication lowers systolic blood pressure to an average below 120 mmHg. A health clinic plans to test this claim by giving the medication to 12 patients and measuring their systolic blood pressure after one month. The average systolic blood pressure for the group was 118.7 mmHg with a standard deviation of 5.7 mmHg. Run the test for the clinic at the \(\alpha = 0.02\) level of significance.
- \(\begin{array}{lcl} H_0 & : & \mu = 120\\ H_a & : & \mu < 120\end{array}\)
- Samples satisfying \(H_a\) are
Completed Example 2: Blood Pressure Medication
Scenario: A pharmaceutical company claims that a new medication lowers systolic blood pressure to an average below 120 mmHg. A health clinic plans to test this claim by giving the medication to 12 patients and measuring their systolic blood pressure after one month. The average systolic blood pressure for the group was 118.7 mmHg with a standard deviation of 5.7 mmHg. Run the test for the clinic at the \(\alpha = 0.02\) level of significance.
- \(\begin{array}{lcl} H_0 & : & \mu = 120\\ H_a & : & \mu < 120\end{array}\)
- Samples satisfying \(H_a\) are
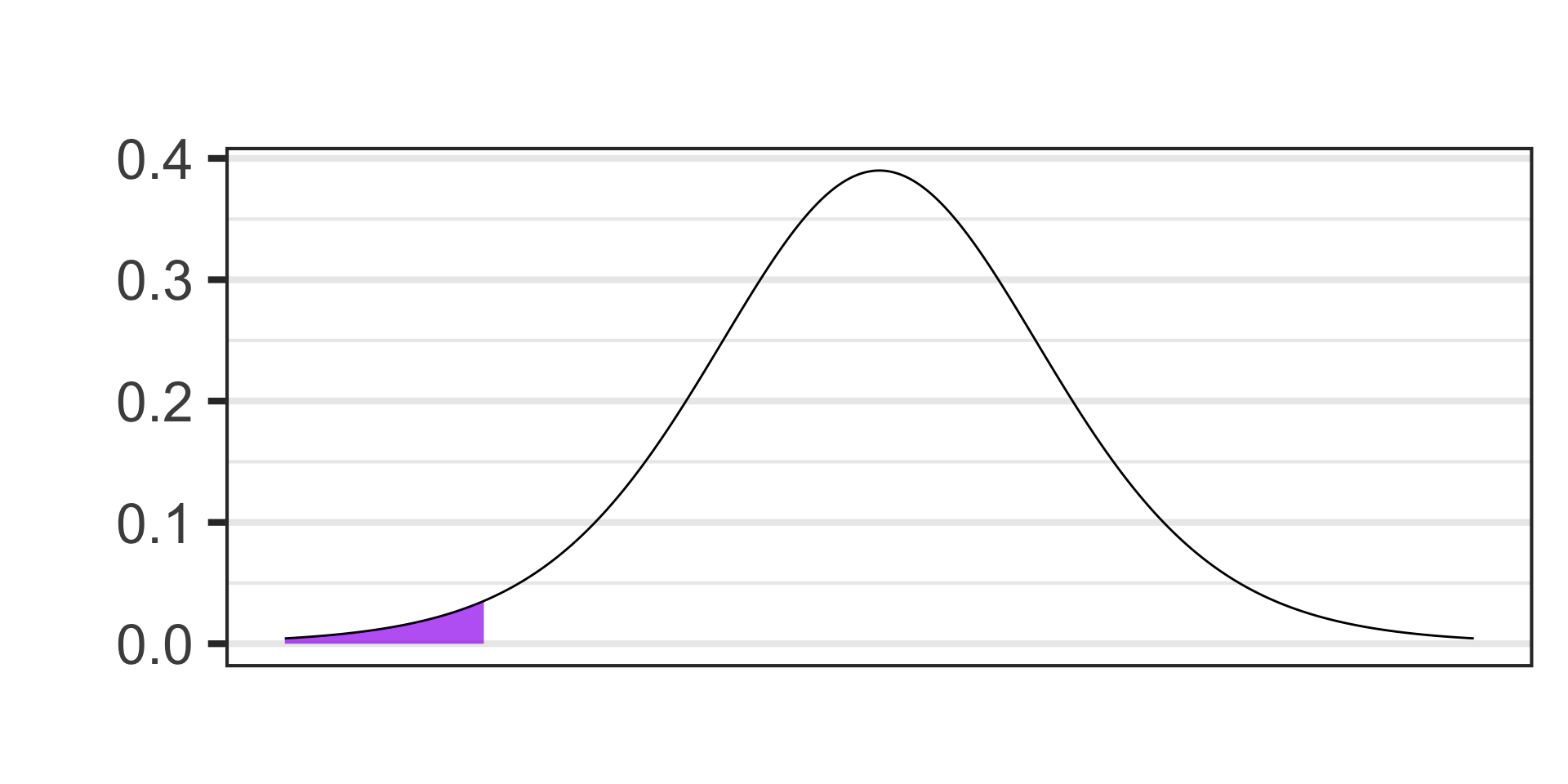
Completed Example 2: Blood Pressure Medication
Scenario: A pharmaceutical company claims that a new medication lowers systolic blood pressure to an average below 120 mmHg. A health clinic plans to test this claim by giving the medication to 12 patients and measuring their systolic blood pressure after one month. The average systolic blood pressure for the group was 118.7 mmHg with a standard deviation of 5.7 mmHg. Run the test for the clinic at the \(\alpha = 0.02\) level of significance.
- \(\begin{array}{lcl} H_0 & : & \mu = 120\\ H_a & : & \mu < 120\end{array}\)
- Samples satisfying \(H_a\) are
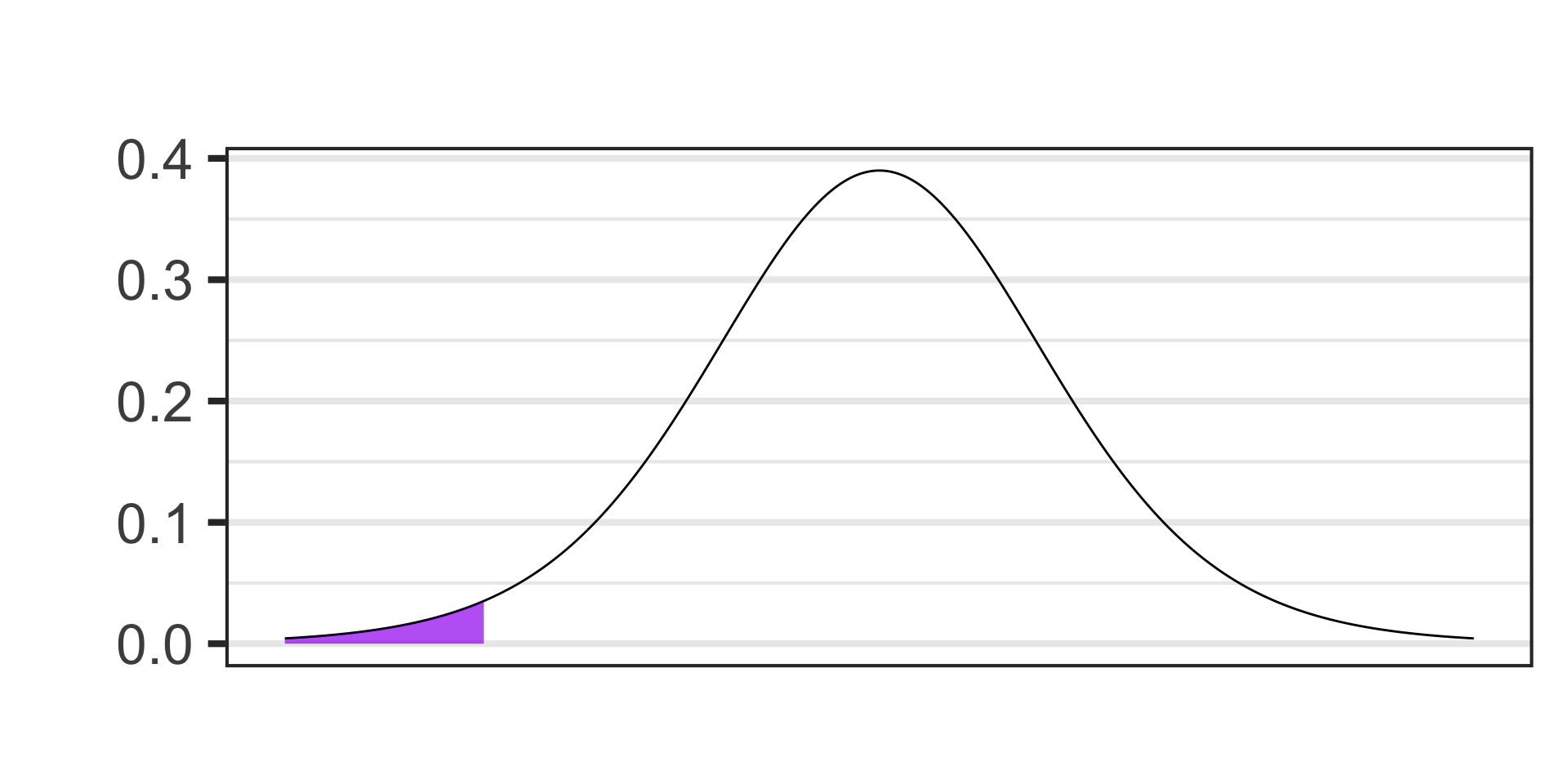
- \(\alpha = 0.02\)
- \(S_E = s/\sqrt{n},~~~\text{df} = n - 1\)
Completed Example 2: Blood Pressure Medication
Scenario: A pharmaceutical company claims that a new medication lowers systolic blood pressure to an average below 120 mmHg. A health clinic plans to test this claim by giving the medication to 12 patients and measuring their systolic blood pressure after one month. The average systolic blood pressure for the group was 118.7 mmHg with a standard deviation of 5.7 mmHg. Run the test for the clinic at the \(\alpha = 0.02\) level of significance.
- \(\begin{array}{lcl} H_0 & : & \mu = 120\\ H_a & : & \mu < 120\end{array}\)
- Samples satisfying \(H_a\) are
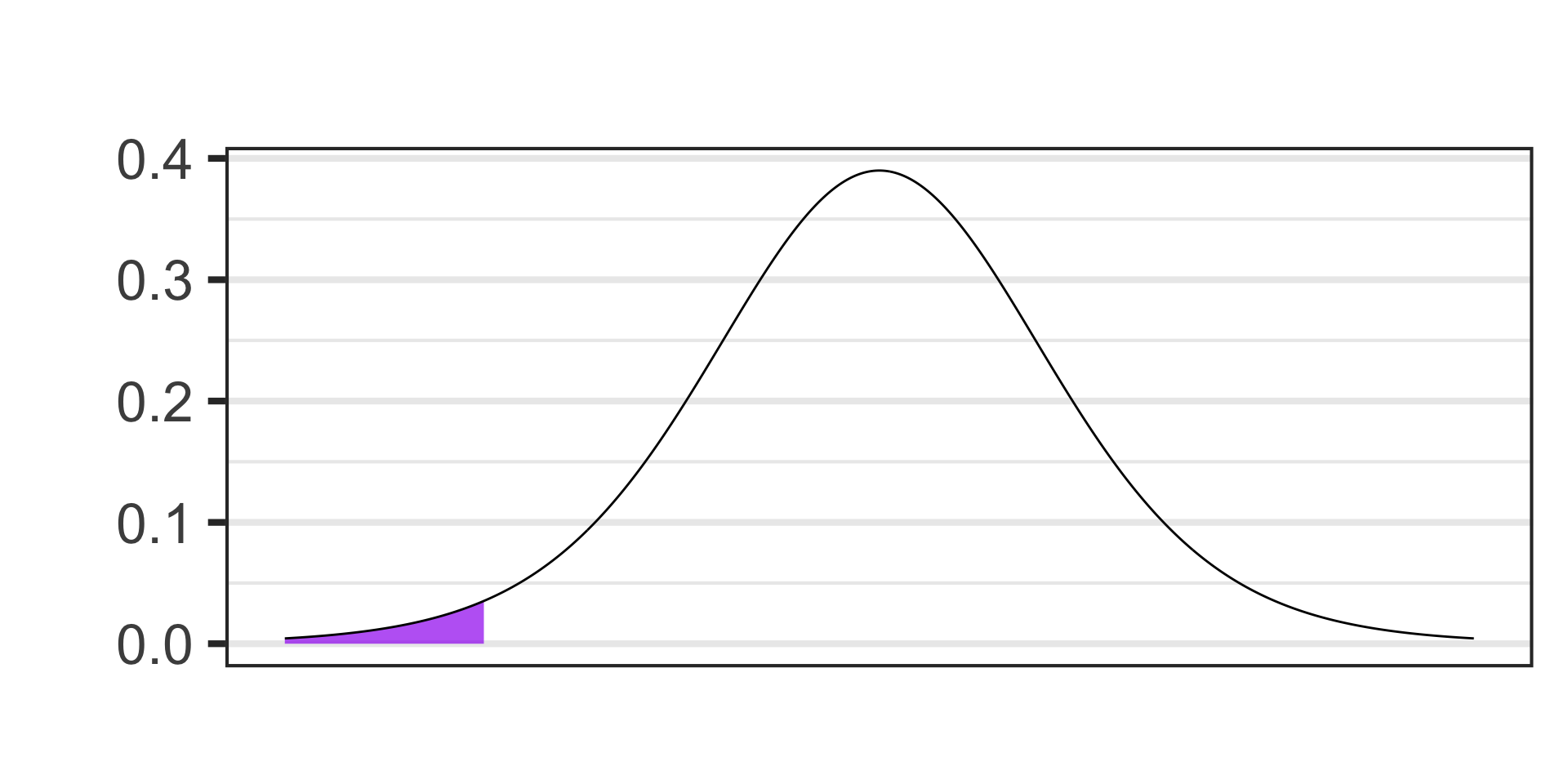
- \(\alpha = 0.02\)
- \(S_E = s/\sqrt{n} = \displaystyle{\frac{5.7}{\sqrt{12}}},~~~\text{df} = n - 1\)
Completed Example 2: Blood Pressure Medication
Scenario: A pharmaceutical company claims that a new medication lowers systolic blood pressure to an average below 120 mmHg. A health clinic plans to test this claim by giving the medication to 12 patients and measuring their systolic blood pressure after one month. The average systolic blood pressure for the group was 118.7 mmHg with a standard deviation of 5.7 mmHg. Run the test for the clinic at the \(\alpha = 0.02\) level of significance.
- \(\begin{array}{lcl} H_0 & : & \mu = 120\\ H_a & : & \mu < 120\end{array}\)
- Samples satisfying \(H_a\) are
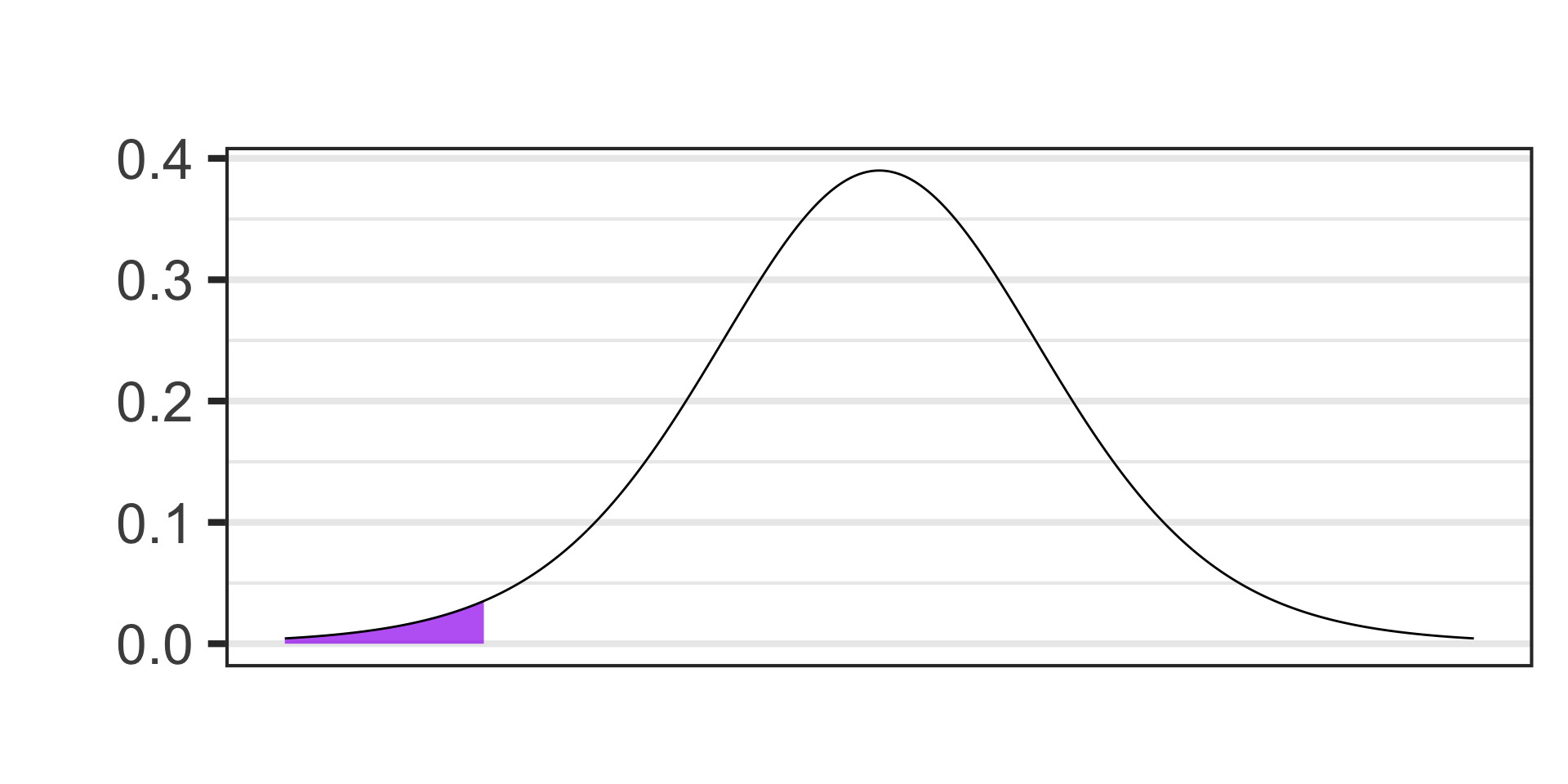
- \(\alpha = 0.02\)
- \(S_E = s/\sqrt{n} \approx 1.6454,~~~\text{df} = n - 1\)
- \(\displaystyle{t = \frac{\left(\text{point est.}\right) - \left(\text{null val.}\right)}{S_E}}\)
Completed Example 2: Blood Pressure Medication
Scenario: A pharmaceutical company claims that a new medication lowers systolic blood pressure to an average below 120 mmHg. A health clinic plans to test this claim by giving the medication to 12 patients and measuring their systolic blood pressure after one month. The average systolic blood pressure for the group was 118.7 mmHg with a standard deviation of 5.7 mmHg. Run the test for the clinic at the \(\alpha = 0.02\) level of significance.
- \(\begin{array}{lcl} H_0 & : & \mu = 120\\ H_a & : & \mu < 120\end{array}\)
- Samples satisfying \(H_a\) are
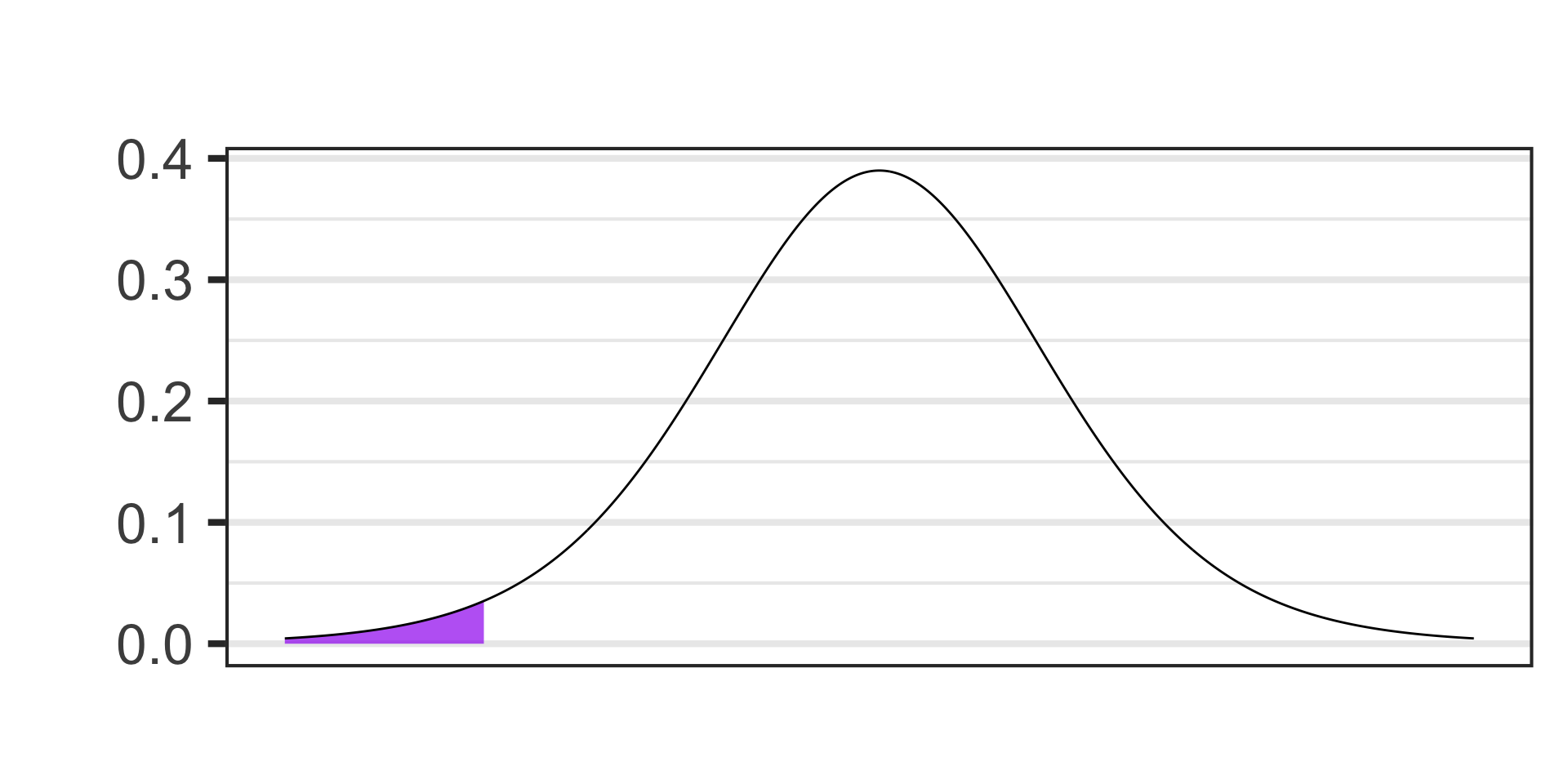
- \(\alpha = 0.02\)
- \(S_E = s/\sqrt{n} \approx 1.6454,~~~\text{df} = n - 1\)
- \(t = \frac{118.7 - 120}{1.6454}\)
Completed Example 2: Blood Pressure Medication
Scenario: A pharmaceutical company claims that a new medication lowers systolic blood pressure to an average below 120 mmHg. A health clinic plans to test this claim by giving the medication to 12 patients and measuring their systolic blood pressure after one month. The average systolic blood pressure for the group was 118.7 mmHg with a standard deviation of 5.7 mmHg. Run the test for the clinic at the \(\alpha = 0.02\) level of significance.
- \(\begin{array}{lcl} H_0 & : & \mu = 120\\ H_a & : & \mu < 120\end{array}\)
- Samples satisfying \(H_a\) are
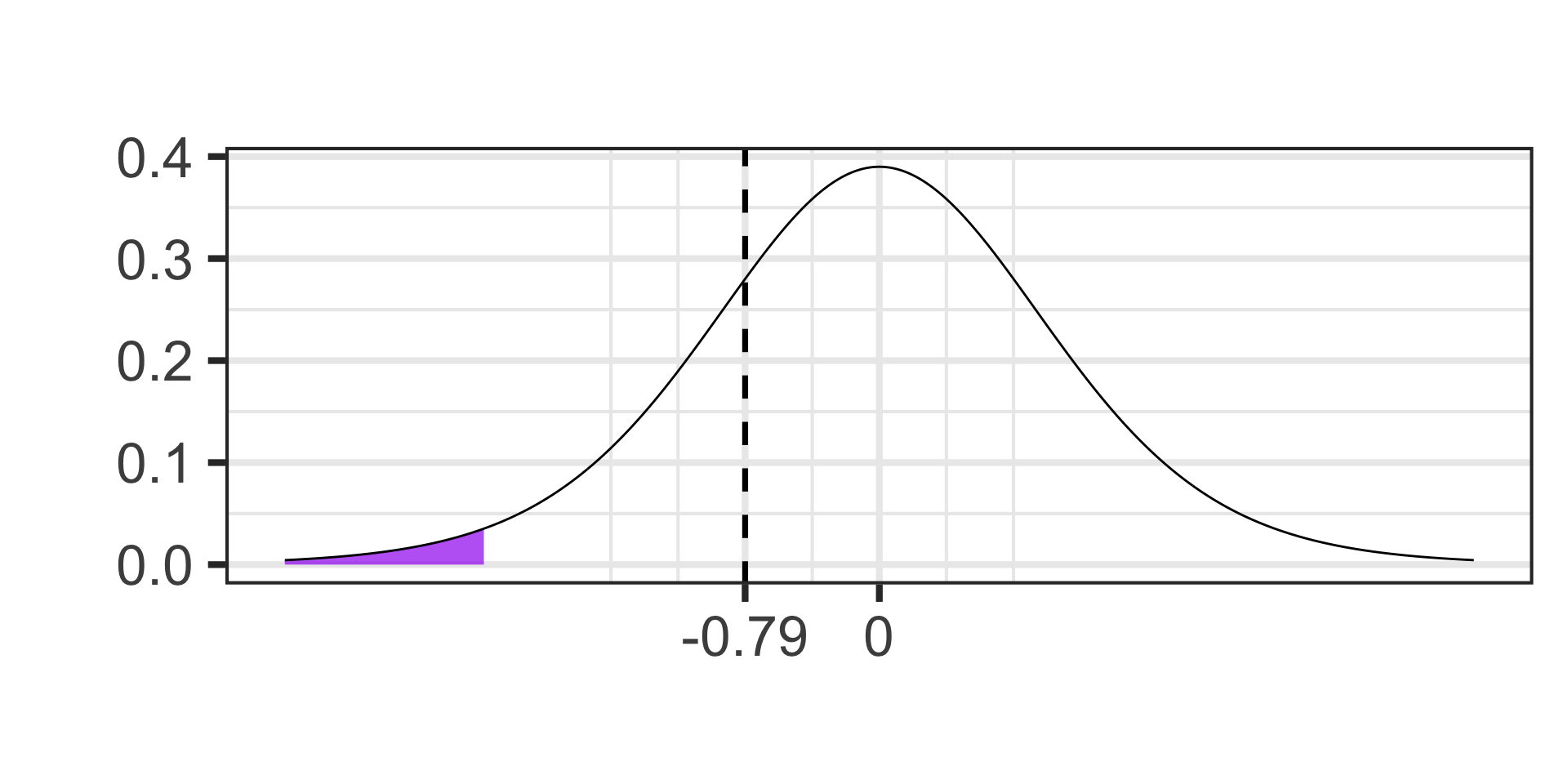
- \(\alpha = 0.02\)
- \(S_E = s/\sqrt{n} \approx 1.6454,~~~\text{df} = n - 1\)
- \(t = \frac{118.7 - 120}{1.6454} \approx -0.79\)
- \(p\)-value \(\approx\)…
Completed Example 2: Blood Pressure Medication
Scenario: A pharmaceutical company claims that a new medication lowers systolic blood pressure to an average below 120 mmHg. A health clinic plans to test this claim by giving the medication to 12 patients and measuring their systolic blood pressure after one month. The average systolic blood pressure for the group was 118.7 mmHg with a standard deviation of 5.7 mmHg. Run the test for the clinic at the \(\alpha = 0.02\) level of significance.
- \(\begin{array}{lcl} H_0 & : & \mu = 120\\ H_a & : & \mu < 120\end{array}\)
- Samples satisfying \(H_a\) are
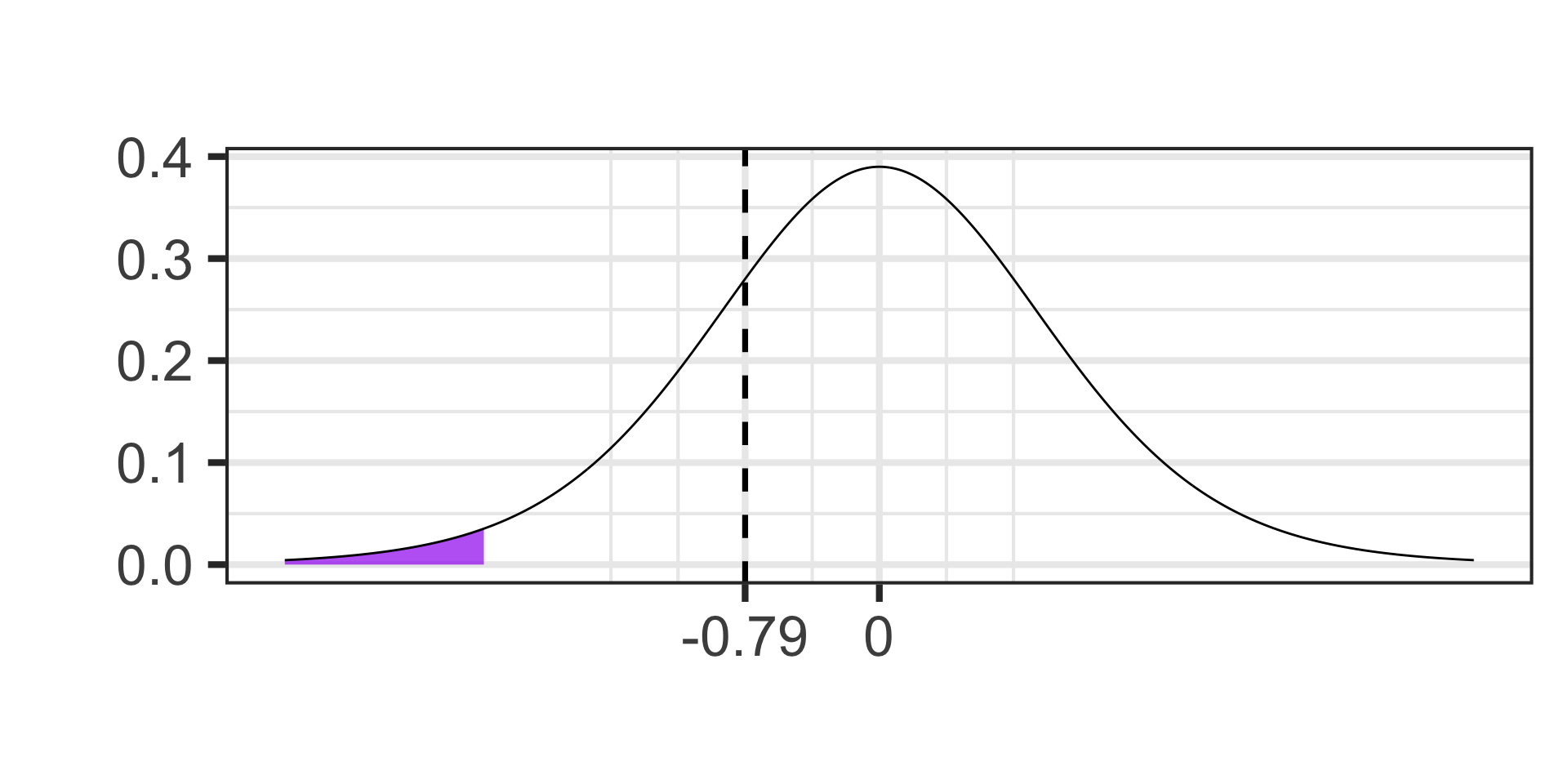
- \(\alpha = 0.02\)
- \(S_E = s/\sqrt{n} \approx 1.6454,~~~\text{df} = n - 1\)
- \(t = \frac{118.7 - 120}{1.6454} \approx -0.79\)
- \(p\)-value \(\approx\)
pt(-0.79, df = 11)\(\approx\) 0.223112
- \(p\)-value \(\geq \alpha\), fail to reject \(H_0\)
- The sample data is compatible with a reality in which the average systolic blood pressure is still 120 mmHg or higher.
A Short Discussion on Statistical Errors
Generally speaking, there are four possible outcomes to a hypothesis test.
| Null Hypothesis (\(H_0\)) is False | Null Hypothesis (\(H_0\)) is True |
|
|---|---|---|
| Reject \(H_0\) | ||
| Do Not Reject \(H_0\) |
A Short Discussion on Statistical Errors
Generally speaking, there are four possible outcomes to a hypothesis test.
| Null Hypothesis (\(H_0\)) is False | Null Hypothesis (\(H_0\)) is True |
|
|---|---|---|
| Reject \(H_0\) | \(\checkmark\) | |
| Do Not Reject \(H_0\) |
A Short Discussion on Statistical Errors
Generally speaking, there are four possible outcomes to a hypothesis test.
| Null Hypothesis (\(H_0\)) is False | Null Hypothesis (\(H_0\)) is True |
|
|---|---|---|
| Reject \(H_0\) | \(\checkmark\) | |
| Do Not Reject \(H_0\) | \(\checkmark\) |
A Short Discussion on Statistical Errors
Generally speaking, there are four possible outcomes to a hypothesis test.
| Null Hypothesis (\(H_0\)) is False | Null Hypothesis (\(H_0\)) is True |
|
|---|---|---|
| Reject \(H_0\) | \(\checkmark\) | Type I Error (False Positive) |
| Do Not Reject \(H_0\) | \(\checkmark\) |
A Short Discussion on Statistical Errors
Generally speaking, there are four possible outcomes to a hypothesis test.
| Null Hypothesis (\(H_0\)) is False | Null Hypothesis (\(H_0\)) is True |
|
|---|---|---|
| Reject \(H_0\) | \(\checkmark\) | Type I Error (False Positive) |
| Do Not Reject \(H_0\) | Type II Error (False Negative) |
\(\checkmark\) |
These erroneous outcomes are no fault of our own
They are the result of sampling error – the randomness associated with the observations that were included as part of our sample, by chance
- The probability of making a Type I Error is \(\alpha\), our level of significance
- The probability of making a Type II Error is often referred to as \(\beta\), and \(1 - \beta\) is called the power of the statistical test – statistical power is beyond the scope of our course, but it is related to the “effect size”, sample size, and the level of significance of the test being run.
Next Up…
Work through some additional practice problems from our long list.
If you want to check your answers, I do have a limited “answer key”, but use it sparingly.
Looking at the key will essentially tell you what type of statistical inference the scenario is requesting from you – that is, if you aren’t confident about determining whether a scenario requires a confidence interval, a hypothesis test, or something else…avoid looking at the answer key and come see me (or go to walk-in tutoring) for help.
You can find the answer key here