Chi-Squared Goodness of Fit and Independence
Inference on Categorical Variables with Multiple Levels
January 3, 2026
Reminder of Inference and Inferential Tools
We use statistical inference to make or test claims about population parameters which we cannot measure directly
- We make claims by constructing confidence intervals
- We test claims by conducting hypothesis tests
Confidence intervals provide a range of plausible values for a population parameter
- They are centered at the point estimate (sample statistic)
- They open up some “wiggle room” called a margin of error, which is influenced by the critical value and the standard error
\[\left(\begin{array}{c}\text{point}\\ \text{estimate}\end{array}\right) \pm \left(\begin{array}{c}\text{critical}\\ \text{value}\end{array}\right)\left(\begin{array}{c}\text{standard}\\ \text{error}\end{array}\right)\]
Reminder of Inference and Inferential Tools
We use statistical inference to make or test claims about population parameters which we cannot measure directly
- We make claims by constructing confidence intervals
- We test claims by conducting hypothesis tests
Confidence intervals provide a range of plausible values for a population parameter
- They are centered at the point estimate (sample statistic)
- They open up some “wiggle room” called a margin of error, which is influenced by the critical value and the standard error
\[\left(\begin{array}{c}\text{point}\\ \text{estimate}\end{array}\right) \pm \boxed{\left(\begin{array}{c}\text{critical}\\ \text{value}\end{array}\right)\left(\begin{array}{c}\text{standard}\\ \text{error}\end{array}\right)}\]
Reminder of Inference and Inferential Tools
We use statistical inference to make or test claims about population parameters which we cannot measure directly
- We make claims by constructing confidence intervals
- We test claims by conducting hypothesis tests
Confidence intervals provide a range of plausible values for a population parameter
- They are centered at the point estimate (sample statistic)
- They open up some “wiggle room” called a margin of error, which is influenced by the critical value and the standard error
\[\left(\begin{array}{c}\text{point}\\ \text{estimate}\end{array}\right) \pm \left(\begin{array}{c}\text{critical}\\ \text{value}\end{array}\right)\left(\begin{array}{c}\text{standard}\\ \text{error}\end{array}\right)\]
Inferential Tools (Continued)
Hypothesis tests provide a framework for testing claims about a population parameter
Assume the claim is false, in reality (null hypothesis)
Measure the probability of observing a sample at least as extreme as ours in that reality (this is called the \(p\)-value)
- If our observed data is “unlikely” (\(p\)-value is lower than the level of significance, \(\alpha\)), then what we’ve observed is incompatible with our assumed reality; we declare evidence that the null hypothesis is false and accept the alternative hypothesis instead
- If our observed data is not “unlikely” (\(p\)-value at least as large as the level of significance), then our observed data is compatible with our assumed reality – we don’t reject the null hypothesis
Where We Are; Where We’re Going…
| Inference On... | Covered |
|---|---|
| One Binary Categorical Variable | ✔ |
| Association Between Two Binary Categorical Variables | ✔ |
Where We Are; Where We’re Going…
| Inference On... | Covered |
|---|---|
| One Binary Categorical Variable | ✔ |
| Association Between Two Binary Categorical Variables | ✔ |
| One MultiClass Categorical Variable | Today |
| Associations Between Two MultiClass Categorical Variables | Today |
Where We Are; Where We’re Going…
| Inference On... | Covered |
|---|---|
| One Binary Categorical Variable | ✔ |
| Association Between Two Binary Categorical Variables | ✔ |
| One MultiClass Categorical Variable | Today |
| Associations Between Two MultiClass Categorical Variables | Today |
| One Numerical Variable | |
| Association Between a Numerical Variable and a Binary Categorical Variable | |
| Association Between a Numerical Variable and a MultiClass Categorical Variable | |
| Association Between a Numerical Variable and a Single Other Numerical Variable | |
| Association Between a Numerical Variable and Many Other Variables |
Where We Are; Where We’re Going…
| Inference On... | Covered |
|---|---|
| One Binary Categorical Variable | ✔ |
| Association Between Two Binary Categorical Variables | ✔ |
| One MultiClass Categorical Variable | Today |
| Associations Between Two MultiClass Categorical Variables | Today |
| One Numerical Variable | |
| Association Between a Numerical Variable and a Binary Categorical Variable | |
| Association Between a Numerical Variable and a MultiClass Categorical Variable | |
| Association Between a Numerical Variable and a Single Other Numerical Variable | |
| Association Between a Numerical Variable and Many Other Variables | |
| Association Between a Categorical Variable and Many Other Variables | ✘ |
Reminder: Inference on a Single Categorical Variable
We’ve been focused on binary (two-class) categorical variables
The single-variable questions we’ve asked are of the form:
Can we estimate the population proportion?
- For example, with 95% confidence, what is the proportion of likely voters in New Hampshire who are planning to vote in favor of Amendment 1?
Is the population proportion greater/less/different than some proposed value?
- For example, is the proportion of likely voters in New Hampshire who favor Amendment 1 at least 66.67%?
But what if we were interested in categorical variables that have more than just two levels?
Are ideological alignments of voting-aged citizens in the US uniformly distributed across the categories very liberal, liberal, moderate, conservative, and very conservative?
Reminder: Inference on Associations Between Two Categorical Variables
Our multivariable questions have been of the form:
Can we estimate the difference in population proportions between Group A and Group B?
- For example, Find a 90% confidence interval for the difference in the proportion of students who feel a sense of belonging at their university between first-year students and seniors.
Is the population proportion in Group A greater/less/different than the population proportion in Group B?
- For example, Is the proportion of students who feel a sense of belonging at their university greater for seniors than for first-year students?
What about associations between categorical variables where at least one has three or more levels?
Is there an association between and individual’s ideology and their perception of the state of their finances (better off, worse off, or about the same) relative to four years ago?
Highlights
Analysing the form of a test statistic
The need for a different test statistic
The need for a new probability distribution
Chi-Squared Tests for Goodness of Fit (inference on a single, multiclass categorical variable)
- A Completed Example
Chi-Squared Tests for Independence (inference on associations between two potentially multiclass categorical variables)
- A Probability Review
- A Completed Example
Additional Examples
A Closer Look at a Test Statistic
So far, I’ve told you that a test statistic takes the form:
\[\begin{array}{c}\text{test}\\ \text{statistic}\end{array} = \frac{\left(\begin{array}{c}\text{point}\\ \text{estimate}\end{array}\right) - \left(\begin{array}{c}\text{null}\\ \text{value}\end{array}\right)}{S_E}\]
- The point estimate comes from our sample data – it is our observed value
- The null value comes from our null hypothesis – it is our expected outcome
Another way to phrase the test statistic formula then is
\[\begin{array}{c}\text{test}\\ \text{statistic}\end{array} = \frac{\text{observed} - \text{expected}}{S_E}\]
For example, if our null hypothesis assumed that 50% of individuals have characteristic “A” and a sample of 200 people included 95 that did, then our observed proportion is 0.475 and our expected proportion was 0.50, so our sample was about 2.5 “percentage points” away from the expected sample.
A New Test Statistic
With binary categorical variables, measuring the proportion associated with just a single category was sufficient – if we know the proportion associated with one outcome, we also know the proportion associated with the other
For example, if we surveyed 100 voters in the US and asked them if they identify more closely with a liberal ideology or a conservative ideology and the results were
| Liberal | Conservative |
|---|---|
| 54 | ? |
Then you know what the full table looks like…
| Liberal | Conservative |
|---|---|
| 54 | 46 |
A New Test Statistic
With binary categorical variables, measuring the proportion associated with just a single category was sufficient – if we know the proportion associated with one outcome, we also know the proportion associated with the other
With multiclass categorical variables, this is not the case. Say we sampled 500 voters about their political ideology.
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| ? | ? | ? | ? | ? |
A New Test Statistic
With binary categorical variables, measuring the proportion associated with just a single category was sufficient – if we know the proportion associated with one outcome, we also know the proportion associated with the other
With multiclass categorical variables, this is not the case. Say we sampled 500 voters about their political ideology.
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 35 | ? | ? | ? | ? |
A New Test Statistic
With binary categorical variables, measuring the proportion associated with just a single category was sufficient – if we know the proportion associated with one outcome, we also know the proportion associated with the other
With multiclass categorical variables, this is not the case. Say we sampled 500 voters about their political ideology.
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 35 | 105 | ? | ? | ? |
A New Test Statistic
With binary categorical variables, measuring the proportion associated with just a single category was sufficient – if we know the proportion associated with one outcome, we also know the proportion associated with the other
With multiclass categorical variables, this is not the case. Say we sampled 500 voters about their political ideology.
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 35 | 105 | 175 | ? | ? |
A New Test Statistic
With binary categorical variables, measuring the proportion associated with just a single category was sufficient – if we know the proportion associated with one outcome, we also know the proportion associated with the other
With multiclass categorical variables, this is not the case. Say we sampled 500 voters about their political ideology.
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 35 | 105 | 175 | 140 | ? |
A New Test Statistic
With binary categorical variables, measuring the proportion associated with just a single category was sufficient – if we know the proportion associated with one outcome, we also know the proportion associated with the other
With multiclass categorical variables, this is not the case. Say we sampled 500 voters about their political ideology.
If political ideology was uniformly distributed, then we would expect:
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| ? | ? | ? | ? | ? |
A New Test Statistic
With binary categorical variables, measuring the proportion associated with just a single category was sufficient – if we know the proportion associated with one outcome, we also know the proportion associated with the other
With multiclass categorical variables, this is not the case. Say we sampled 500 voters about their political ideology.
If political ideology was uniformly distributed, then we would expect:
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 100 | 100 | 100 | 100 | 100 |
But what if we observed:
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 35 | 105 | 175 | 140 | 45 |
A New Test Statistic
Expected results from 500 surveyed individuals:
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 100 | 100 | 100 | 100 | 100 |
Observed results from 500 surveyed individuals:
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 35 | 105 | 175 | 140 | 45 |
Comparing a single observed value to a single expected value is no longer enough to describe our scenario
We could calculate the difference observed - expected for each group though
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 35 - 100 = -65 | 105 - 100 = 5 | 175 - 100 = 75 | 140 - 100 = 40 | 45 - 100 = -55 |
A New Test Statistic
Differences (observed - expected) in results from 500 surveyed individuals:
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| -65 | 5 | 75 | 40 | -55 |
We need some way to combine/summarize these deviations.
A New Test Statistic
Differences (observed - expected) in results from 500 surveyed individuals:
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| -65 | 5 | 75 | 40 | -55 |
We need some way to combine/summarize these deviations. If we just add these up, we’ll get 0 because the positive and negative differences will cancel one another out.
“Small” deviations are unsurprising, while “large” deviations should be more rare. To emphasize this, we’ll square the differences, penalizing larger deviations more heavily.
A “large” deviation is relative – a deviation of 50 is very large if the expected count was only 20 to begin with, but a deviation of 50 is quite small if the expected count was 1000. We’ll divide each squared deviation by the expected count to compensate for this.
Our resulting test statistic for this scenario takes the form
\[\sum_{i = 1}^{k}{\frac{\left(\text{observed} - \text{expected}\right)^2}{\text{expected}}}\]
where \(k\) is the number of categories/groups.
The Chi-Squared Distribution
This new test statistic doesn’t follow a normal distribution.
The Chi-Squared Distribution
This new test statistic doesn’t follow a normal distribution. It instead follows a Chi-Squared distribution.
Actually, the Chi-Squared distribution isn’t a single distribution – it is a family of distributions defined by a single parameter…degrees of freedom.
We’ll talk more about degrees of freedom when we get to the actual tests but, for now, here are a few Chi-Squared distributions.
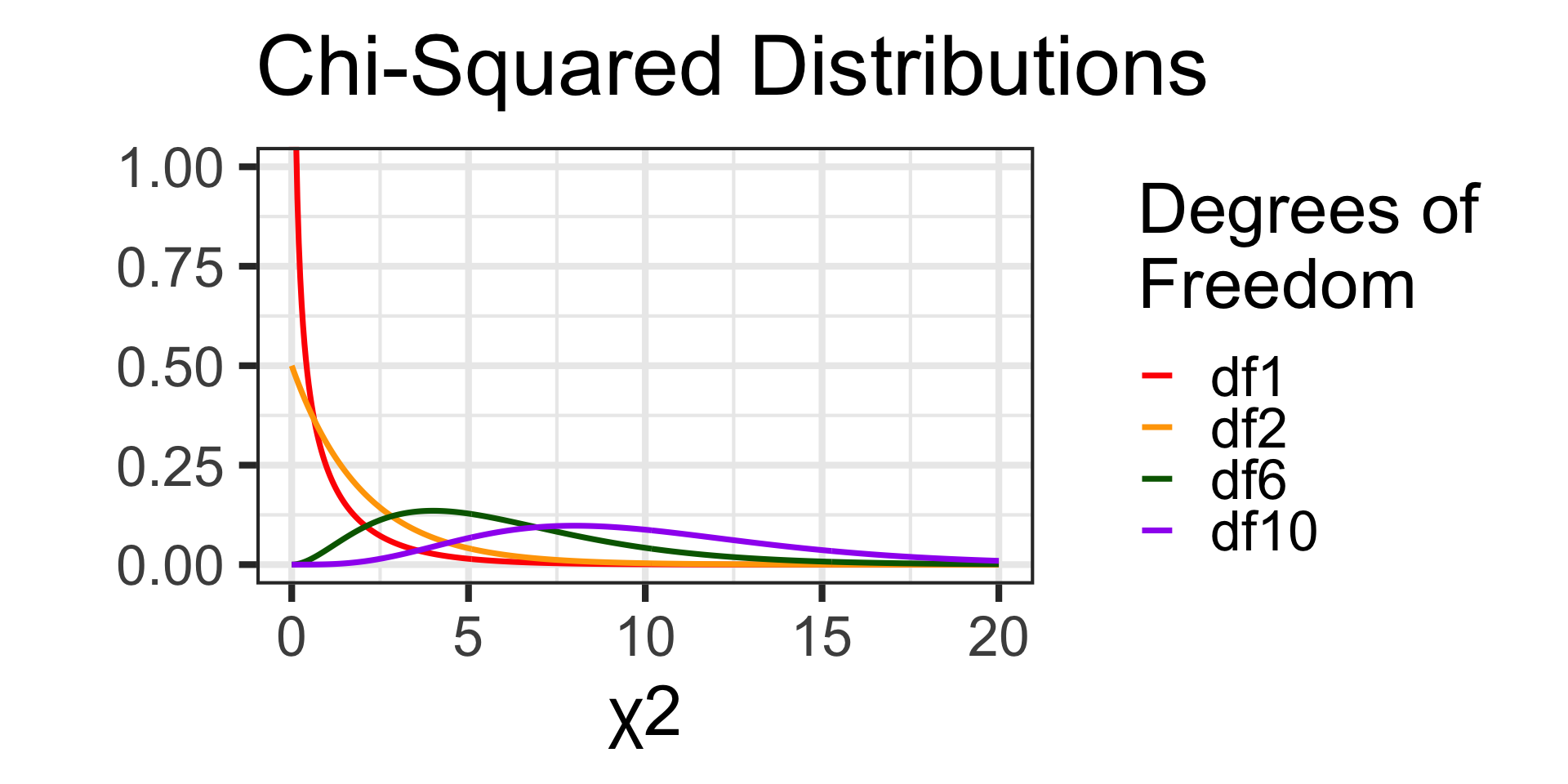
The Chi-Squared Distribution
This new test statistic doesn’t follow a normal distribution. It instead follows a Chi-Squared distribution.
Actually, the Chi-Squared distribution isn’t a single distribution – it is a family of distributions defined by a single parameter…degrees of freedom.
We’ll talk more about degrees of freedom when we get to the actual tests but, for now, here are a few Chi-Squared distributions.
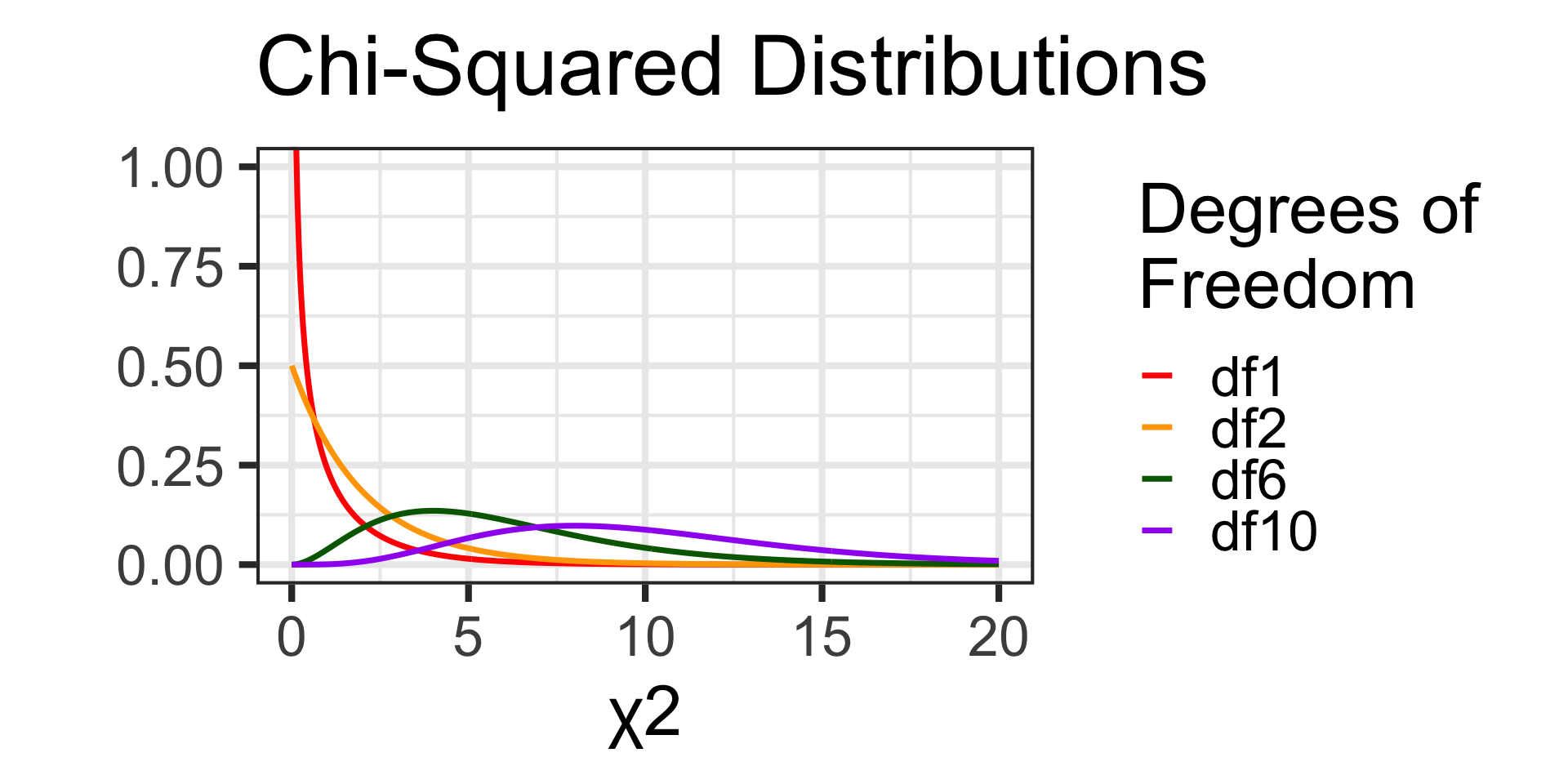
The Chi-Squared distributions are defined over non-negative numbers only, are right-skewed, and [for our course] we’ll only ever be interested in the area in the right tail.
The Chi-Squared Distribution
This new test statistic doesn’t follow a normal distribution. It instead follows a Chi-Squared distribution.
Actually, the Chi-Squared distribution isn’t a single distribution – it is a family of distributions defined by a single parameter…degrees of freedom.
We’ll talk more about degrees of freedom when we get to the actual tests but, for now, here are a few Chi-Squared distributions.
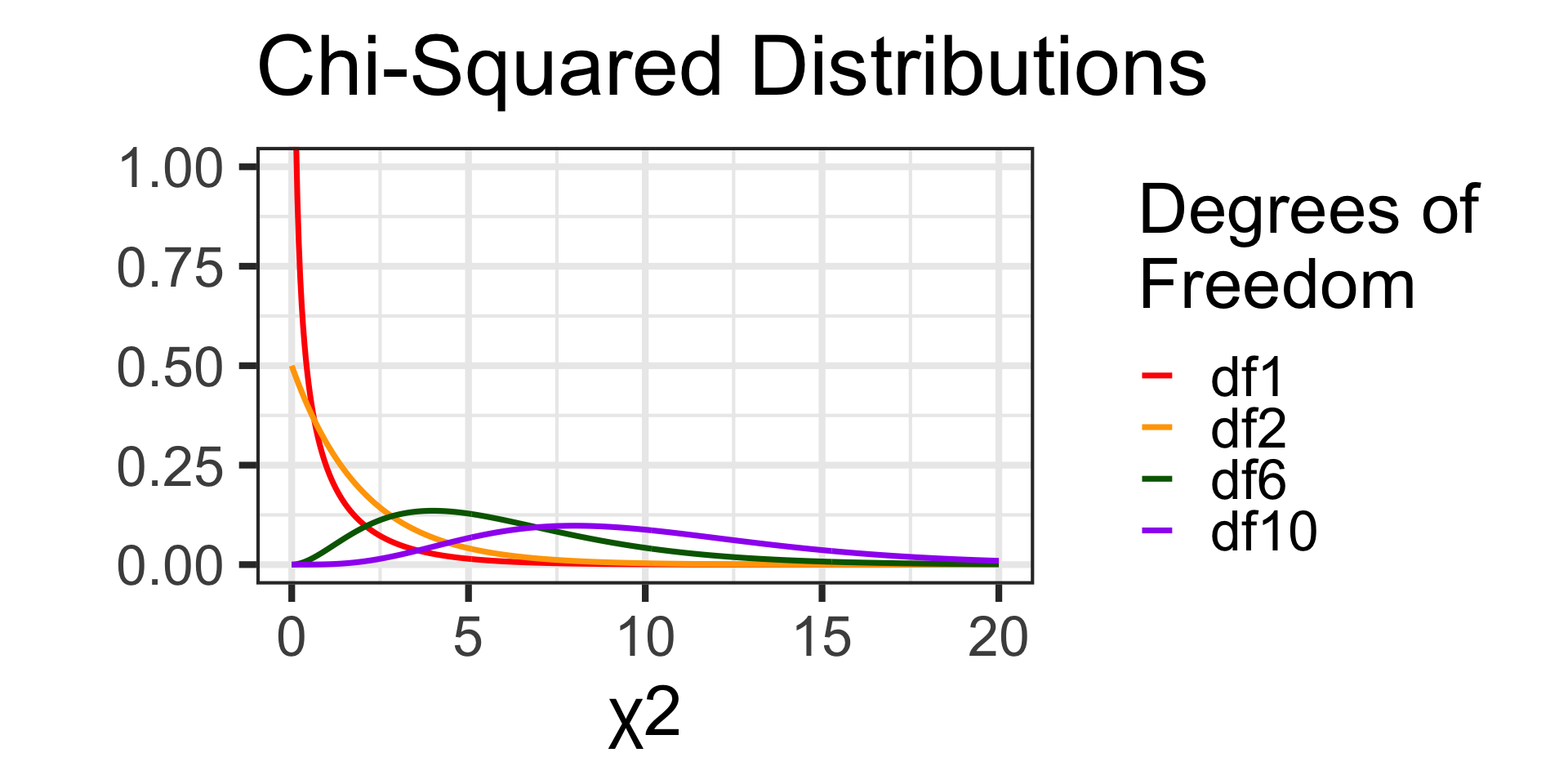
The Chi-Squared distributions are defined over non-negative numbers only, are right-skewed, and [for our course] we’ll only ever be interested in the area in the right tail.
1 - pchisq(q, df)
A Completed Example: Chi-Squared Test for Goodness of Fit
Scenario: We wonder if political ideologies (very liberal, liberal, moderate, conservative, or very conservative) are uniformly distributed. We collect data from a random sample of 500 individuals and observe the following results
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative |
|---|---|---|---|---|
| 35 | 105 | 175 | 140 | 45 |
Run a test at the \(\alpha = 0.05\) level of significance to determine whether the distribution of political ideologies is uniform.
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
A Completed Example: Chi-Squared Test for Goodness of Fit
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
Recall the table of differences from earlier
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative | |
|---|---|---|---|---|---|
| Observed | 35 | 105 | 175 | 140 | 45 |
| Expected | 100 | 100 | 100 | 100 | 100 |
| Difference | -65 | 5 | 75 | 40 | -55 |
\[\begin{array}{c}\text{test}\\ \text{statistic}\end{array} = \sum_{i = 1}^{5}{\frac{\left(\text{observed} - \text{expected}\right)^2}{\text{expected}}}\]
A Completed Example: Chi-Squared Test for Goodness of Fit
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
Recall the table of differences from earlier
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative | |
|---|---|---|---|---|---|
| Observed | 35 | 105 | 175 | 140 | 45 |
| Expected | 100 | 100 | 100 | 100 | 100 |
| Difference | -65 | 5 | 75 | 40 | -55 |
\[\begin{array}{c}\text{test}\\ \text{statistic}\end{array} = \frac{\left(-65\right)^2}{100} + \frac{5^2}{100} + \frac{75^2}{100} + \frac{40^2}{100} + \frac{\left(-55\right)^2}{100}\]
A Completed Example: Chi-Squared Test for Goodness of Fit
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
Recall the table of differences from earlier
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative | |
|---|---|---|---|---|---|
| Observed | 35 | 105 | 175 | 140 | 45 |
| Expected | 100 | 100 | 100 | 100 | 100 |
| Difference | -65 | 5 | 75 | 40 | -55 |
\[\begin{array}{c}\text{test}\\ \text{statistic}\end{array} = 145\]
A Completed Example: Chi-Squared Test for Goodness of Fit
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
Recall the table of differences from earlier
| Very Liberal | Liberal | Moderate | Conservative | Very Conservative | |
|---|---|---|---|---|---|
| Observed | 35 | 105 | 175 | 140 | 45 |
| Expected | 100 | 100 | 100 | 100 | 100 |
| Difference | -65 | 5 | 75 | 40 | -55 |
\[\begin{array}{c}\text{test}\\ \text{statistic}\end{array} = \frac{\left(-65\right)^2}{100} + \frac{5^2}{100} + \frac{75^2}{100} + \frac{40^2}{100} + \frac{\left(-55\right)^2}{100} = \boxed{~145~}\]
A Completed Example: Chi-Squared Test for Goodness of Fit
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
\[\chi^2~\text{test statistic} = 145\]
- Calculate the \(p\)-value using the Chi-Squared distribution
A Completed Example: Chi-Squared Test for Goodness of Fit
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
\[\chi^2~\text{test statistic} = 145\]
- Calculate the \(p\)-value using the Chi-Squared distribution with degrees of freedom equal to one less than the number of groups (\(k - 1\))
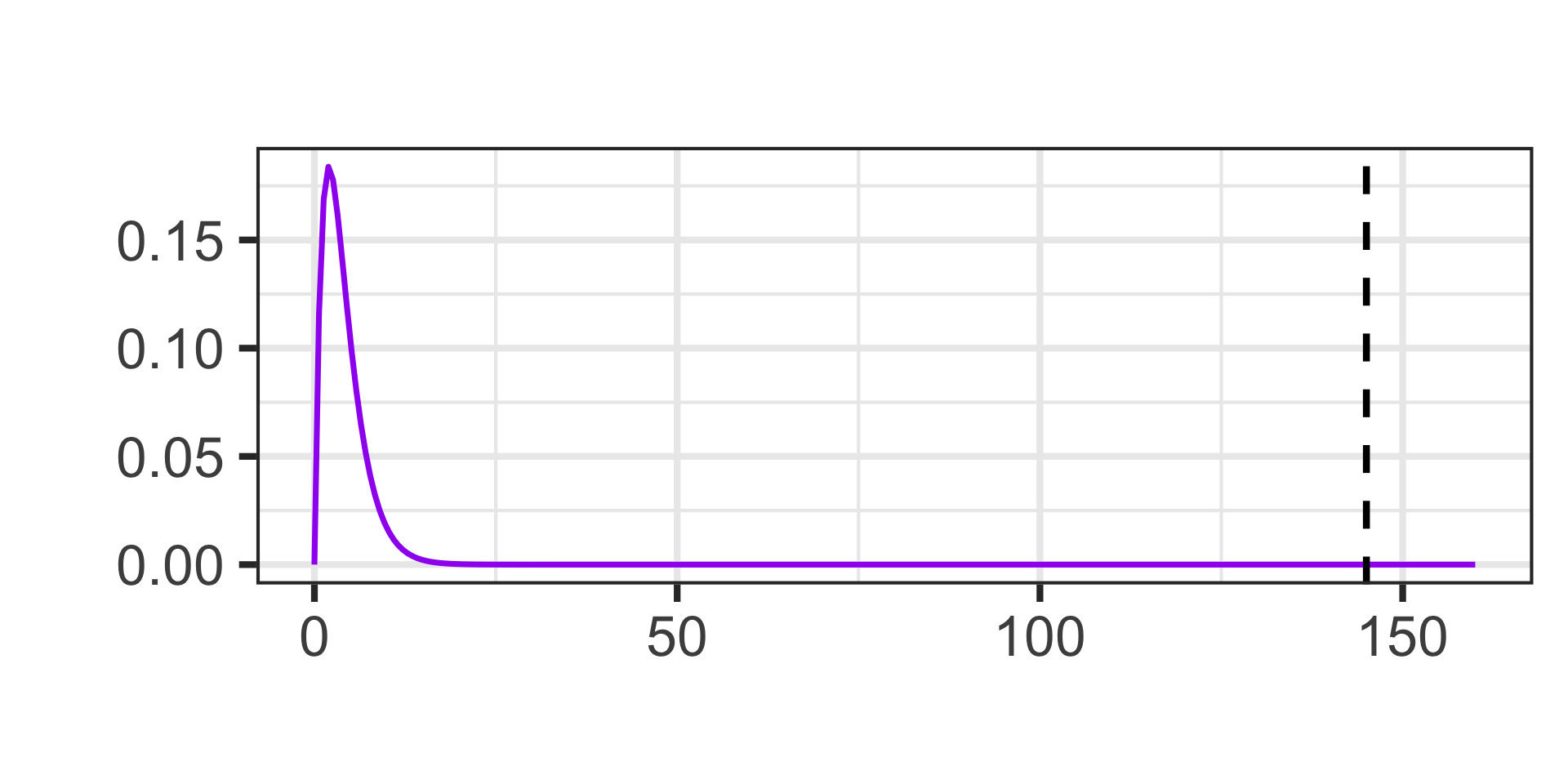
A Completed Example: Chi-Squared Test for Goodness of Fit
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
\[\chi^2~\text{test statistic} = 145\]
- Calculate the \(p\)-value using the Chi-Squared distribution with degrees of freedom equal to one less than the number of groups (\(k - 1\))
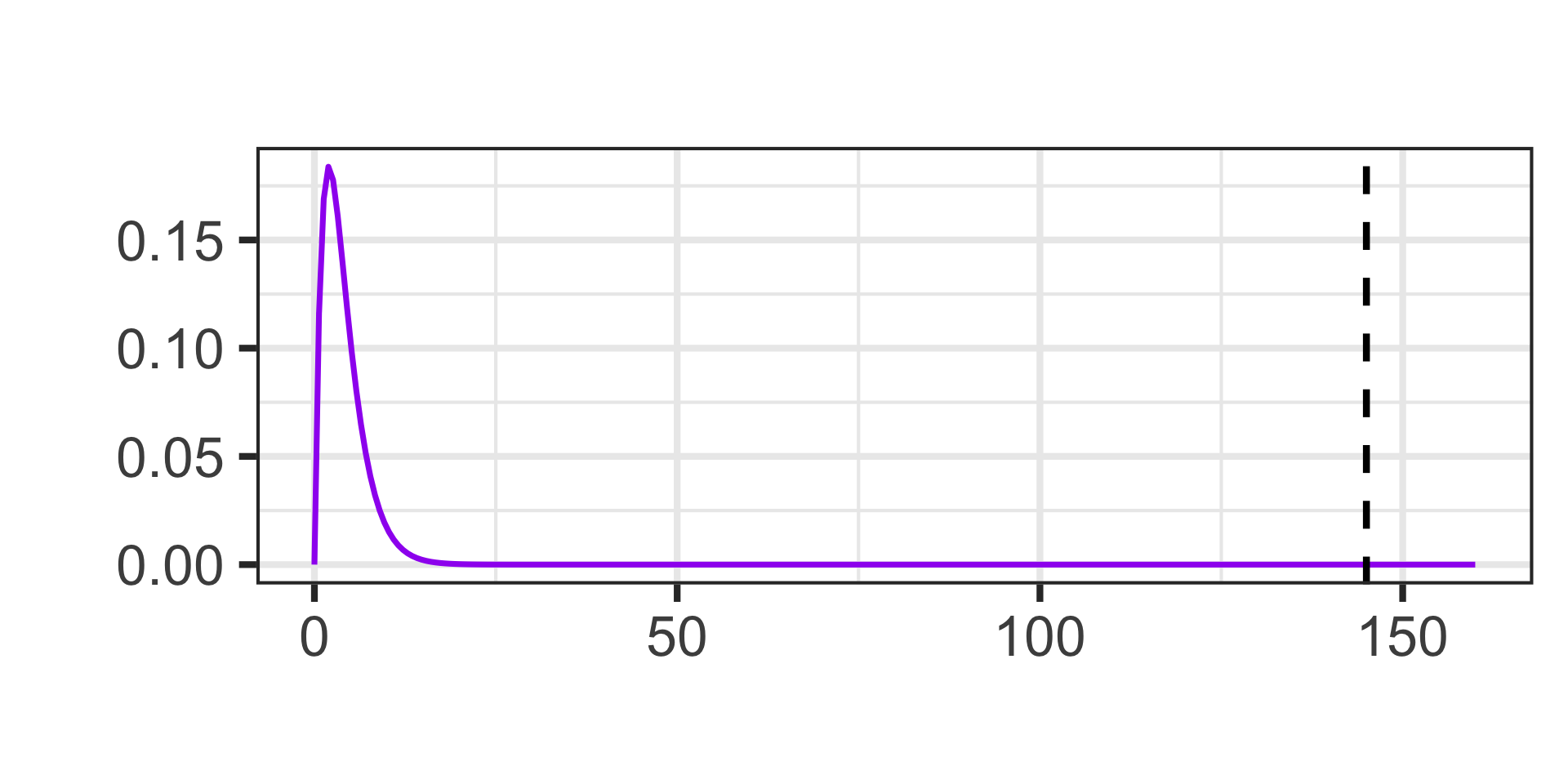
1 - pchisq(145, df = 5 - 1) \(\approx\) 0
A Completed Example: Chi-Squared Test for Goodness of Fit
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
\[\chi^2~\text{test statistic} = 145\]
Note: Remember that a reported \(p\)-value of “0” means that the \(p\)-value is extremely small and is being rounded to 0 – it is not possible to have a \(p\)-value which is 0 exactly.
- Calculate the \(p\)-value using the Chi-Squared distribution with degrees of freedom equal to one less than the number of groups (\(k - 1\))
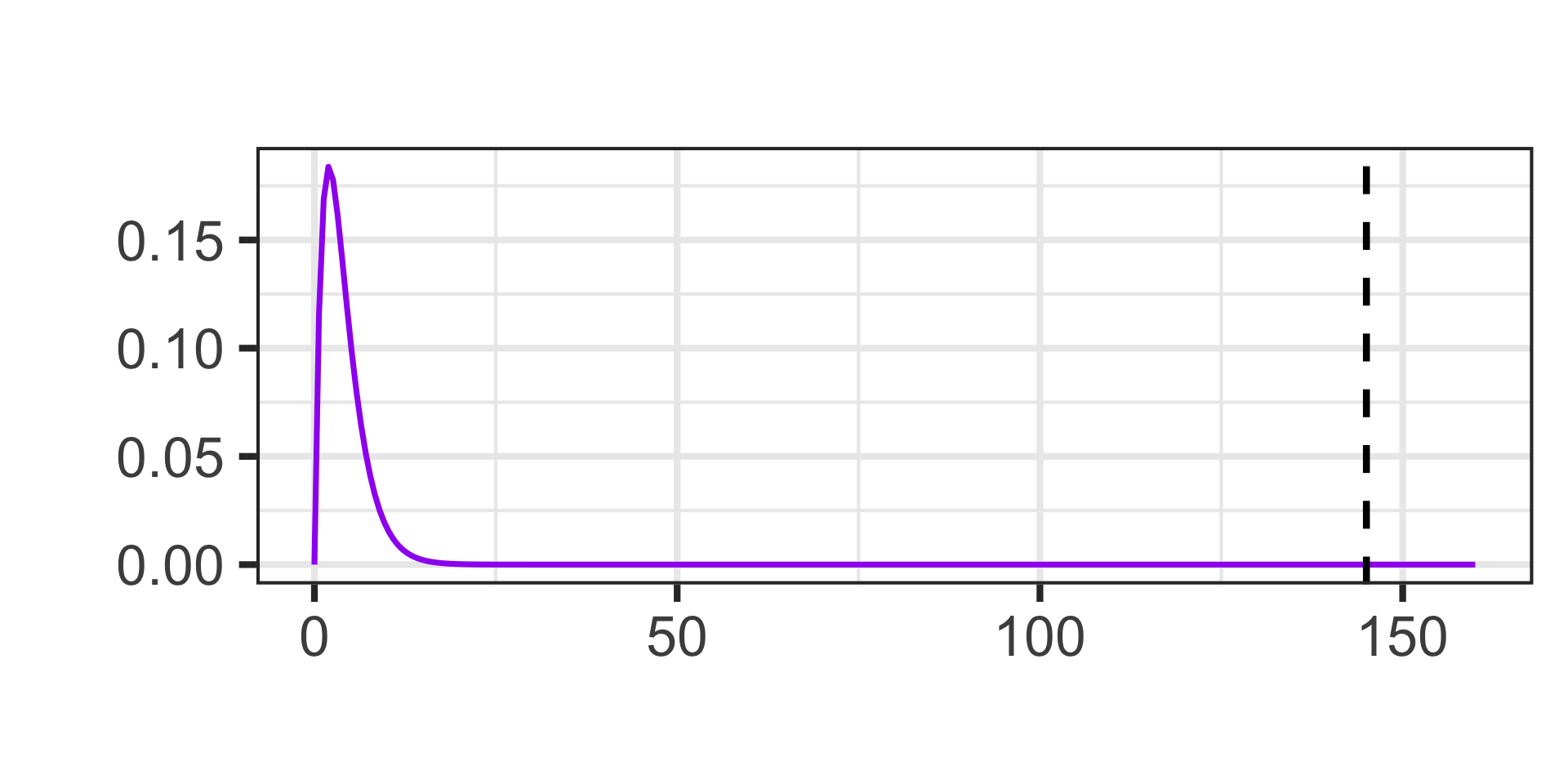
1 - pchisq(145, df = 5 - 1) \(\approx\) 0
A Completed Example: Chi-Squared Test for Goodness of Fit
- \(\begin{array}{lcl} H_0 & : & \text{The distribution is uniform}\\ H_a & : & \text{The distribution is not uniform}\end{array}\)
- Set the level of significance at \(\alpha = 0.05\)
- Calculate the test statistic
\[\chi^2~\text{test statistic} = 145\]
- The \(p\)-value is less than \(0.05\) (our desired level of significance), so we reject the null hypothesis and accept the alternative
- The observed data are not compatible with political ideologies being distributed uniformly. The distribution is different.
- Calculate the \(p\)-value using the Chi-Squared distribution with degrees of freedom equal to one less than the number of groups (\(k - 1\))
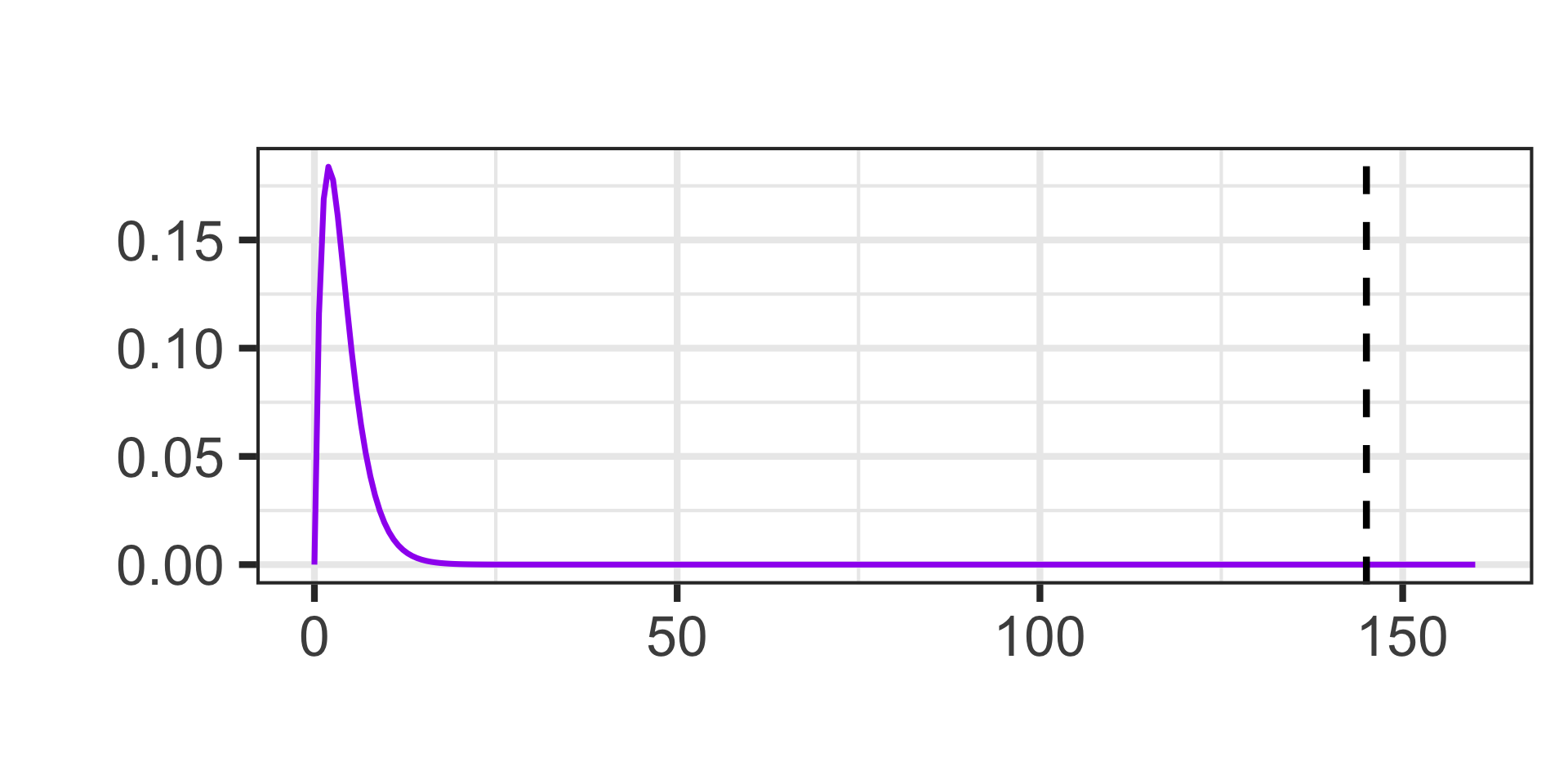
1 - pchisq(145, df = 5 - 1) \(\approx\) 0
Recap: Chi-Squared Goodness of Fit
We now have an ability to test whether the levels of a categorical variable over a population follow a particular distribution
Here, we tested for a uniform distribution, but we can test any generic distribution we like – the choice just influences how we calculate our expected counts
Recap: Chi-Squared Goodness of Fit
We now have an ability to test whether the levels of a categorical variable over a population follow a particular distribution
The strategy for testing Goodness of Fit follows the same general structure as the hypothesis tests we’ve seen previously: read the scenario, write the hypotheses, declare the level of significance (\(\alpha\)), calculate the test statistic, convert it to a \(p\)-value, compare the \(p\)-value to \(\alpha\), and interpret the result of the test in context
The main differences were:
The null hypothesis assumes the questioned distribution rather than assuming a claim is false.
The test statistic is a \(\chi^2\) test statistic, taking the form \(\displaystyle{\sum_{i = 1}^{k}{\frac{\left(\text{observed} - \text{expected}\right)^2}{\text{expected}}}}\)
The \(p\)-value is computed using the Chi-Squared distribution and we are always interested in the right tail; we use
1 - pchisq(test_statistic, df)- The degrees of freedom (
df) is one less than the number of levels/groups under the categorical variable whose distribution we are testing.
- The degrees of freedom (
Chi-Squared Tests for Independence
Now that we know how to perform statistical inference to test the distribution of a single categorical variable with multiple (more than two) classes, we can use a similar strategy to test for associations between two categorical variables where at least one has more than two classes.
The main differences are:
- The hypotheses will be \(\begin{array}{lcl} H_0 & : & \text{The two variables are independent}\\ H_a & : & \text{An association exists between the two variables}\end{array}\)
- The tables for our observed and expected counts will be organized in both rows and columns
- Assuming that the first categorical variable has \(k\) levels and the second categorical variable has \(\ell\) levels, the degrees of freedom for the Chi-Squared distribution in this scenario will be \(\left(k - 1\right)\cdot \left(\ell - 1\right)\).
We’ll quickly review how to work with a “two-way table”, calculating probabilities of independent events, and calculating expected value before heading into an example.
Probability Review
A two-way table is a way to summarize data observed with respect to two categorical variables – its rows correspond to the levels of one of the categorical variables and its columns correspond to levels of the other categorical variable.
Consider the two-way table below which shows species of bird and the type of feeder they were observed feeding from.
| Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total | |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
Probability Review
Consider the two-way table below which shows species of bird and the type of feeder they were observed feeding from.
| Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total | |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
The probability of a randomly selected bird being a Hummingbird is
The probability of a randomly selected bird being found at a nectar feeder is
\[\mathbb{P}\left[\text{Hummingbird}\right] = \frac{80}{305} \approx 0.2262\]
\[\mathbb{P}\left[\text{Nectar Feeder}\right] = \frac{90}{305} \approx 0.2951\]
Probability Review
Consider the two-way table below which shows species of bird and the type of feeder they were observed feeding from.
| Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total | |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
Assuming that species and feeder preference are independent, the probability of a randomly selected bird being a hummingbird and being found at a nectar feeder would be
\[\mathbb{P}\left[\text{Hummingbird and Nectar Feeder}\right] = \mathbb{P}\left[\text{Hummingbird}\right]\cdot\mathbb{P}\left[\text{Nectar Feeder}\right]\]
Probability Review
Consider the two-way table below which shows species of bird and the type of feeder they were observed feeding from.
| Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total | |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
Assuming that species and feeder preference are independent, the probability of a randomly selected bird being a hummingbird and being found at a nectar feeder would be
\[\mathbb{P}\left[\text{Hummingbird and Nectar Feeder}\right] = \left(\frac{80}{305}\right)\cdot\left(\frac{90}{305}\right)\]
Probability Review
Consider the two-way table below which shows species of bird and the type of feeder they were observed feeding from.
| Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total | |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
Assuming that species and feeder preference are independent, the probability of a randomly selected bird being a hummingbird and being found at a nectar feeder would be
\[\mathbb{P}\left[\text{Hummingbird and Nectar Feeder}\right] \approx 0.0774\]
Probability Review
Consider the two-way table below which shows species of bird and the type of feeder they were observed feeding from.
| Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total | |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
Assuming that species and feeder preference are independent, the expected number of hummingbirds observed at the nectar feeder would be:
\[n\cdot\mathbb{P}\left[\text{Hummingbird and Nectar Feeder}\right] \approx 305\cdot 0.0774\]
Probability Review
Consider the two-way table below which shows species of bird and the type of feeder they were observed feeding from.
| Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total | |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
Assuming that species and feeder preference are independent, the expected number of hummingbirds observed at the nectar feeder would be:
\[n\cdot\mathbb{P}\left[\text{Hummingbird and Nectar Feeder}\right] \approx 23.607\]
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
| Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total | |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- We’ll calculate the test statistic, but we’ll need the observed and expected counts for each cell in the table first…
A Completed Example: Chi-Squared Test for Independence
| Observed Counts | Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
| Expected Counts | Seed Feeder |
Nectar Feeder |
Fruit Feeder |
|---|---|---|---|
| Finches | \(305\cdot\left(\frac{85}{305}\right)\cdot\left(\frac{115}{305}\right)\) | \(305\cdot\left(\frac{85}{305}\right)\cdot\left(\frac{90}{305}\right)\) | \(305\cdot\left(\frac{85}{305}\right)\cdot\left(\frac{100}{305}\right)\) |
| Hummingbirds | \(305\cdot\left(\frac{80}{305}\right)\cdot\left(\frac{115}{305}\right)\) | \(305\cdot\left(\frac{80}{305}\right)\cdot\left(\frac{90}{305}\right)\) | \(305\cdot\left(\frac{80}{305}\right)\cdot\left(\frac{100}{305}\right)\) |
| Orioles | \(305\cdot\left(\frac{85}{305}\right)\cdot\left(\frac{115}{305}\right)\) | \(305\cdot\left(\frac{85}{305}\right)\cdot\left(\frac{90}{305}\right)\) | \(305\cdot\left(\frac{85}{305}\right)\cdot\left(\frac{100}{305}\right)\) |
| Woodpeckers | \(305\cdot\left(\frac{55}{305}\right)\cdot\left(\frac{115}{305}\right)\) | \(305\cdot\left(\frac{55}{305}\right)\cdot\left(\frac{90}{305}\right)\) | \(305\cdot\left(\frac{55}{305}\right)\cdot\left(\frac{100}{305}\right)\) |
A Completed Example: Chi-Squared Test for Independence
| Observed Counts | Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
| Expected Counts | Seed Feeder |
Nectar Feeder |
Fruit Feeder |
|---|---|---|---|
| Finches | 32.05 | 25.08 | 27.87 |
| Hummingbirds | 30.16 | 23.61 | 26.23 |
| Orioles | 32.05 | 25.08 | 27.87 |
| Woodpeckers | 20.74 | 16.23 | 18.03 |
A Completed Example: Chi-Squared Test for Independence
| Observed Counts | Seed Feeder |
Nectar Feeder |
Fruit Feeder |
Total |
|---|---|---|---|---|
| Finches | 60 | 15 | 10 | 85 |
| Hummingbirds | 5 | 70 | 5 | 80 |
| Orioles | 20 | 5 | 60 | 85 |
| Woodpeckers | 30 | 0 | 25 | 55 |
| Total | 115 | 90 | 100 | 305 |
Note: Be sure to exclude the total entries when you store the observed values
A Completed Example: Chi-Squared Test for Independence
| Expected Counts | Seed Feeder |
Nectar Feeder |
Fruit Feeder |
|---|---|---|---|
| Finches | 32.05 | 25.08 | 27.87 |
| Hummingbirds | 30.16 | 23.61 | 26.23 |
| Orioles | 32.05 | 25.08 | 27.87 |
| Woodpeckers | 20.74 | 16.23 | 18.03 |
Note: Be sure to input the expected counts in the same order that you used for the observed counts – otherwise you won’t be comparing the right cells to one another.
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- We’ll calculate the test statistic, but we’ll need the observed and expected counts for each cell in the table first…
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- We’ll calculate the test statistic, since we have our
observedandexpectedcounts
Remember that the Chi-Squared test statistic is \(\displaystyle{\sum{\frac{\left(\text{observed} - \text{expected}\right)^2}{\text{expected}}}}\)
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- The Chi-Squared test statistic is about 249.91
- The degrees of freedom for the test is \(\left(k - 1\right)\cdot\left(\ell - 1\right)\)
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- The Chi-Squared test statistic is about 249.91
- The degrees of freedom for the test is \(\left(4 - 1\right)\cdot\left(3 - 1\right) = 6\)
- Now we’ll calculate the \(p\)-value
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- The Chi-Squared test statistic is about 249.91
- The degrees of freedom for the test is \(\left(4 - 1\right)\cdot\left(3 - 1\right) = 6\)
- Now we’ll calculate the \(p\)-value
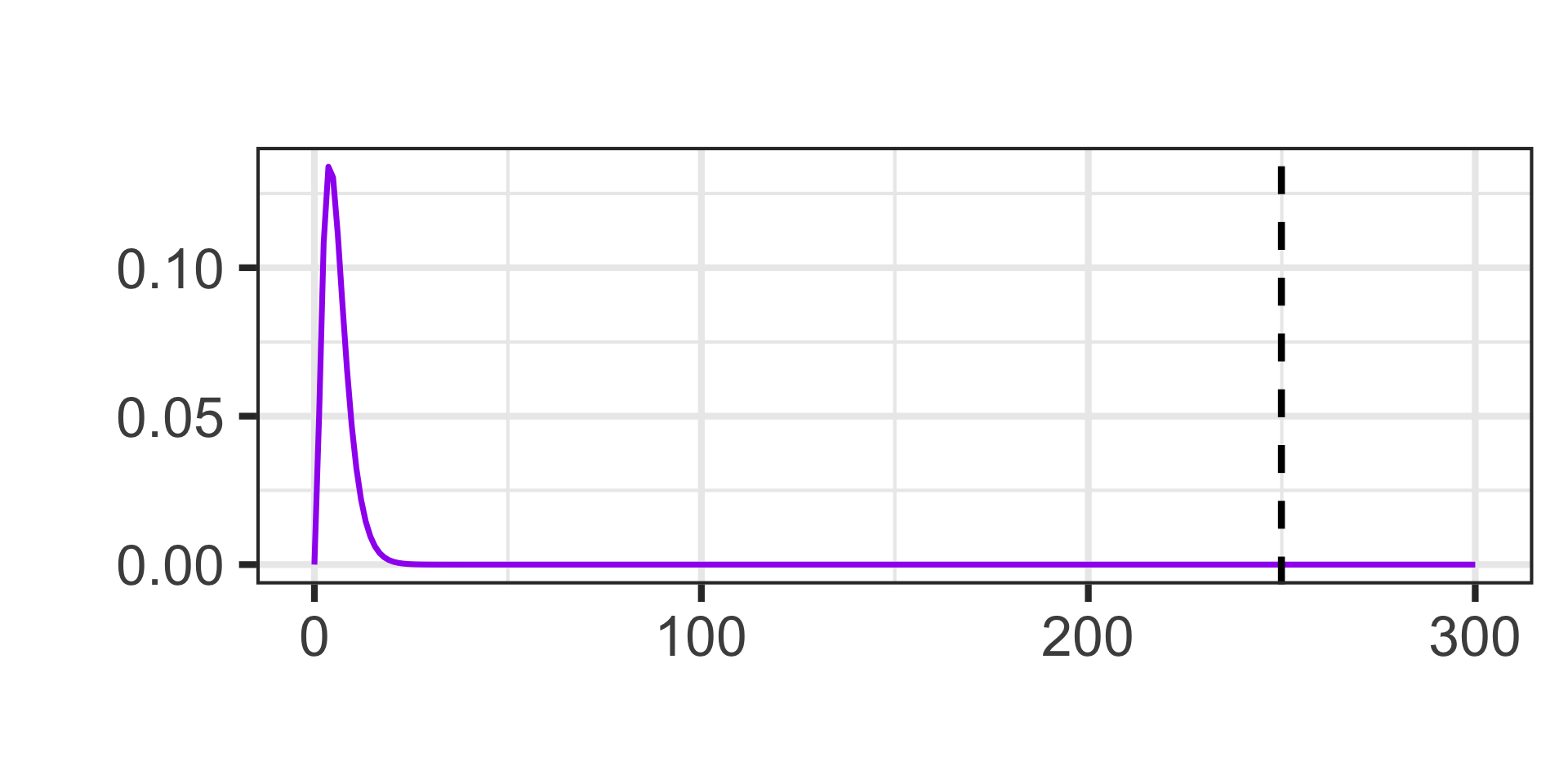
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- The Chi-Squared test statistic is about 249.91
- The degrees of freedom for the test is \(\left(4 - 1\right)\cdot\left(3 - 1\right) = 6\)
- Now we’ll calculate the \(p\)-value
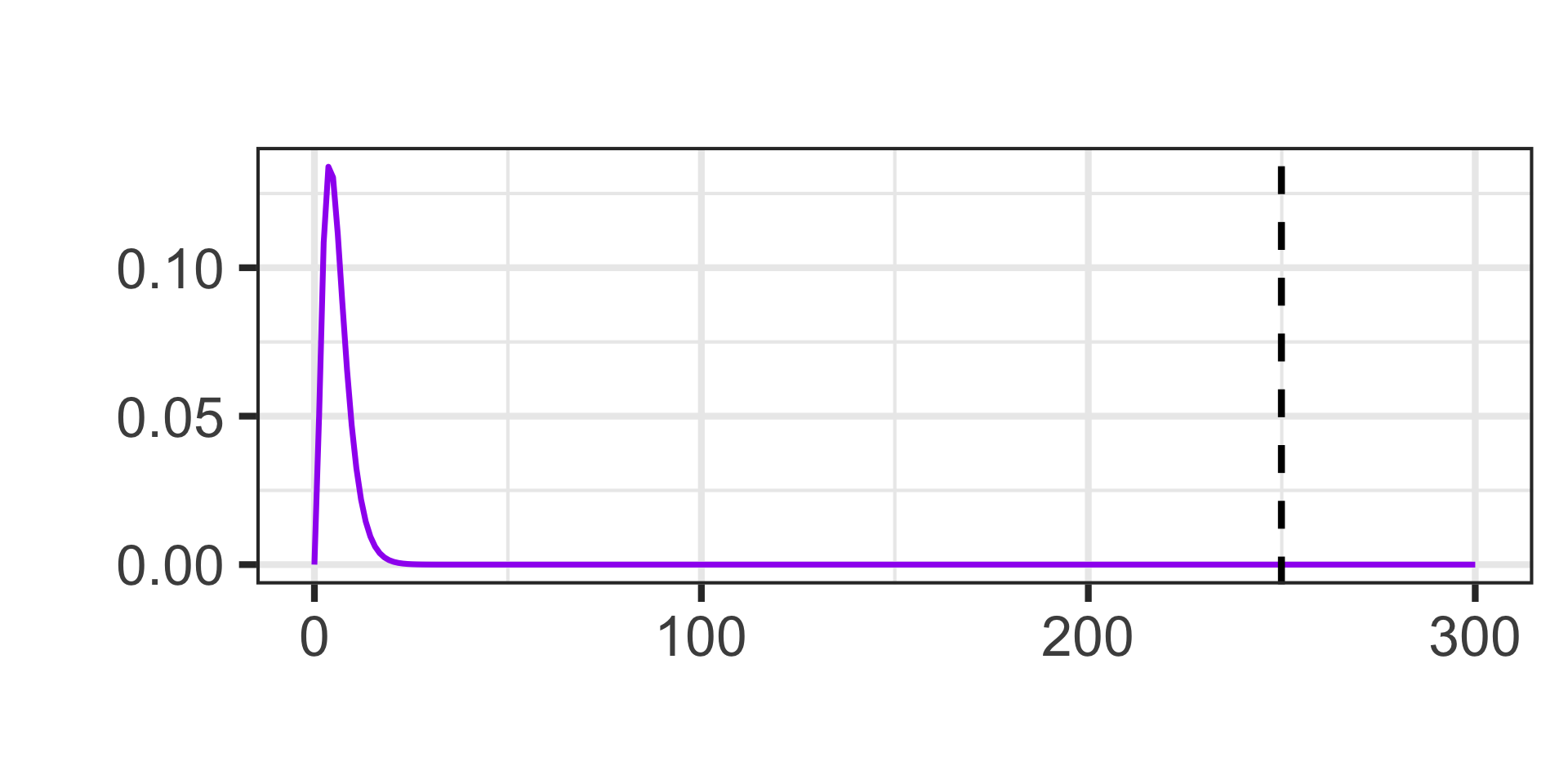
1 - pchisq(249.91, df = 6) \(\approx\) 0
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- The Chi-Squared test statistic is about 249.91
- The degrees of freedom for the test is \(\left(4 - 1\right)\cdot\left(3 - 1\right) = 6\)
- Again, the \(p\)-value is so small that it rounds to 0
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- The Chi-Squared test statistic is about 249.91
- The degrees of freedom for the test is \(\left(4 - 1\right)\cdot\left(3 - 1\right) = 6\)
- Again, the \(p\)-value is so small that it rounds to 0
- The \(p\)-value is less than the level of significance, so we reject \(H_0\) and accept \(H_a\)
A Completed Example: Chi-Squared Test for Independence
Scenario: A wildlife researcher is studying whether different bird species have distinct feeding preferences among three types of feeders: Seed Feeder, Nectar Feeder, and Fruit Feeder. The researcher observes four bird species in a particular park: Finches, Hummingbirds, Orioles, and Woodpeckers. Over several days, the researcher records the feeder each bird species prefers in the table below. Test whether species and feeding preference are independent at the 10% level of significance.
- The hypotheses are \(\begin{array}{lcl} H_0 & : & \text{Species and feeder preference are independent}\\ H_a & : & \text{Species and feeder preference are associated}\end{array}\)
- The level of significance is \(\alpha = 0.10\)
- The Chi-Squared test statistic is about 249.91
- The degrees of freedom for the test is \(\left(4 - 1\right)\cdot\left(3 - 1\right) = 6\)
- Again, the \(p\)-value is so small that it rounds to 0
- The \(p\)-value is less than the level of significance, so we reject \(H_0\) and accept \(H_a\)
- This sample provides evidence to suggest that bird species and feeding preference are associated
Examples to Try: Streaming Service Popularity
Scenario: A media company expects certain subscription preferences among viewers for various streaming services: Netflix, Hulu, Amazon Prime, and Disney+, with expected preferences of 40%, 25%, 20%, and 15%, respectively. A sample of 500 viewers reveals the following counts:
| Streaming Service | Observed Count |
|---|---|
| Netflix | 210 |
| Hulu | 130 |
| Amazon Prime | 100 |
| Disney+ | 60 |
Conduct a test at the 5% level of significance to determine whether the sample provides evidence against this expected distribution.
Examples to Try: Department and Work Arrangement
Scenario: A company wants to investigate if employees’ work arrangement preferences (In-office, Hybrid, or Remote) vary by department (IT, Marketing, HR). A survey of 300 employees yields the following results:
| In-office | Hybrid | Remote | Total | |
|---|---|---|---|---|
| IT | 30 | 60 | 40 | 130 |
| Marketing | 25 | 35 | 30 | 90 |
| HR | 20 | 25 | 35 | 80 |
| Total | 75 | 120 | 105 | 300 |
Conduct a test at the 1% level of significance to determine whether this data provides evidence to suggest that work arrangements are different across departments.
Examples to Try: Student Major versus Preferred Social Media Platform
Scenario: A university wants to see if there’s a link between students’ major category (STEM, Arts, Business, Humanities) and their preferred social media platform (Instagram, TikTok, Twitter, LinkedIn). They survey 200 students and gather the following results back:
| TikTok | Total | ||||
|---|---|---|---|---|---|
| STEM | 20 | 15 | 30 | 35 | 100 |
| Arts | 15 | 25 | 20 | 5 | 65 |
| Business | 10 | 5 | 15 | 25 | 55 |
| Humanities | 5 | 5 | 10 | 5 | 25 |
| Total | 50 | 50 | 75 | 70 | 200 |
Examples to Try: Voting Method Preferences
Scenario: An electoral commission wants to verify if voter preferences for different voting methods in a city (In-person, Mail-in, Drop-off, Online) match their pre-election forecast based on trends in similar areas. They projected that 50% would prefer in-person voting, 20% mail-in, 15% drop-off, and 15% online. A random sample of 1000 likely voters revealed the following preferences.
| Voting Method | Observed Count | Expected Percentage |
|---|---|---|
| In-person | 520 | 50% |
| Mail-in | 200 | 20% |
| Drop-off | 150 | 15% |
| Online | 130 | 15% |
| Total | 1,000 |
Does the sample provide evidence against their projections?
Exit Ticket Task
Navigate to our MAT241 Exit Ticket Form, answer the questions, and complete the task below.
Note. Today’s discussion is listed as 13. Chi-Square Goodness of Fit and Independence

Task: A public health researcher wants to check whether the distribution of blood types among patients at a community clinic matches the known distribution of the general population (45% O, 40% A, 10% B, 5% AB). In a random sample of 200 clinic patients there were 78 type O, 92 type A, 22 type B, and 8 type AB.
- What are the hypotheses to test the researcher’s question of interest?
- Carry out the test and determine the conclusion.
Next Time…
Inference on Numerical Variables