Practicing Inference with Categorical Data
One- and Two-Proportion Inference
October 24, 2024
Reminder: Framework for Constructing Confidence Intervals
General Strategy: Each time we seek to Construct a confidence interval, we will…
- Read the scenario very carefully
- Determine what it is we are trying to estimate – a mean? a proportion? a difference in means or proportions?
- Recall the general “formula” for the confidence interval
\[\scriptsize{\left(\begin{array}{c}\texttt{point}\\ \texttt{estimate}\end{array}\right) \pm \left(\begin{array}{c}\texttt{critical}\\ \texttt{value}\end{array}\right)\cdot S_E}\]
- Re-read the scenario to identify the point estimate, which comes from the sample data
- Use the Standard Error Decision Tree to find how to compute the standard error (\(S_E\))
- Identify or compute the appropriate critical value
- Find the lower- and upper-bounds for the confidence interval by evaluating the “formula”
- Interpret the confidence interval in the appropriate context
Reminder: Hypothesis Testing Framework
General Strategy: Each time we conduct a hypothesis test, we will…
Read the scenario carefully and determine whether you are testing a claim about a mean, a proportion, comparison of means, or comparison of proportions.
Identify the claim being tested and state the null hypothesis (\(H_0\)) and alternative hypothesis (\(H_a\)). The null hypothesis represents the “status quo” or “no difference” and always involves an equal sign, while the alternative hypothesis is the claim to be tested and involves one of: \(<,~>,~\neq\)
Draw a picture of your alternative hypothesis, shading in the tails corresponding to samples that would satisfy the alternative hypothesis.
Set the level of significance (\(\alpha\)) for the test. The level of significance is the “cut-off” for a sample being unusual/unlikely/unexpected. The standard cutoff is \(\alpha = 0.05\), unless we are told otherwise.
Compute the test statistic, where \(\displaystyle{\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}}\)
- The point estimate comes from the sample data
- The null value comes from the null hypothesis
- The standard error (\(S_E\)) formula is found on the Standard Error Decision Tree
The test statistic is just a boundary value, use it along with your picture from step 3 to calculate a \(p\)-value (the probability of observing data at least as extreme as ours if the null hypothesis were true).
Compare your \(p\)-value to the level of significance (\(\alpha\)) demanded by your test and make a decision about whether or not to reject the null hypothesis.
Interpret the result of your hypothesis test in the context appropriate for your scenario.
Inference on a Single Proportion versus Comparisons of Proportions
At our last class meeting, we saw one example of the construction of a confidence interval and another example conducting a hypothesis test
In both of those scenarios, the population parameter of interest was a single population proportion
We’ll see scenarios like this again today, but we’ll also consider scenarios in which we’d like to compare two population proportions.
The general procedures for constructing confidence intervals or conducting hypothesis tests are the same in both scenarios, except that in the comparison scenarios…
- the population parameter of interest is the difference in proportions between the two sub-populations
- the formula for computing the standard error (\(S_E\)) is different
Navigating the Standard Error Tree
One of the main purposes of the Standard Error Decision Tree document is to help you identify the appropriate standard error (\(S_E\)) to use in your calculation of a confidence interval or test statistic
To navigate the tree, begin from the box at the top, which asks whether we are working with means (\(\mu\)) or proportions (\(p\))
Follow your answer down the tree and continue answering the questions until you land inside a box with a standard error formula (\(S_E = \cdots\))
The side of the tree for working with proportions is less complicated than the side for means – we’ll stick to proportions for now
At this point, we’ll either calculate \(\displaystyle{S_E = \sqrt{\frac{p\left(1 - p\right)}{n}}}\) for a single proportion or \(\displaystyle{S_E = \sqrt{\frac{p_1\left(1 - p_1\right)}{n_1} + \frac{p_2\left(1 - p_2\right)}{n_2}}}\) for a comparison between two population proportions
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
- We’re testing a claim comparing two population
proportions - The hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\)
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
- We’re testing a claim comparing two population
proportions - The hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)
- See the picture of the alternative hypothesis below:
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
We’re testing a claim comparing two population
proportionsThe hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)See the picture of the alternative hypothesis below:
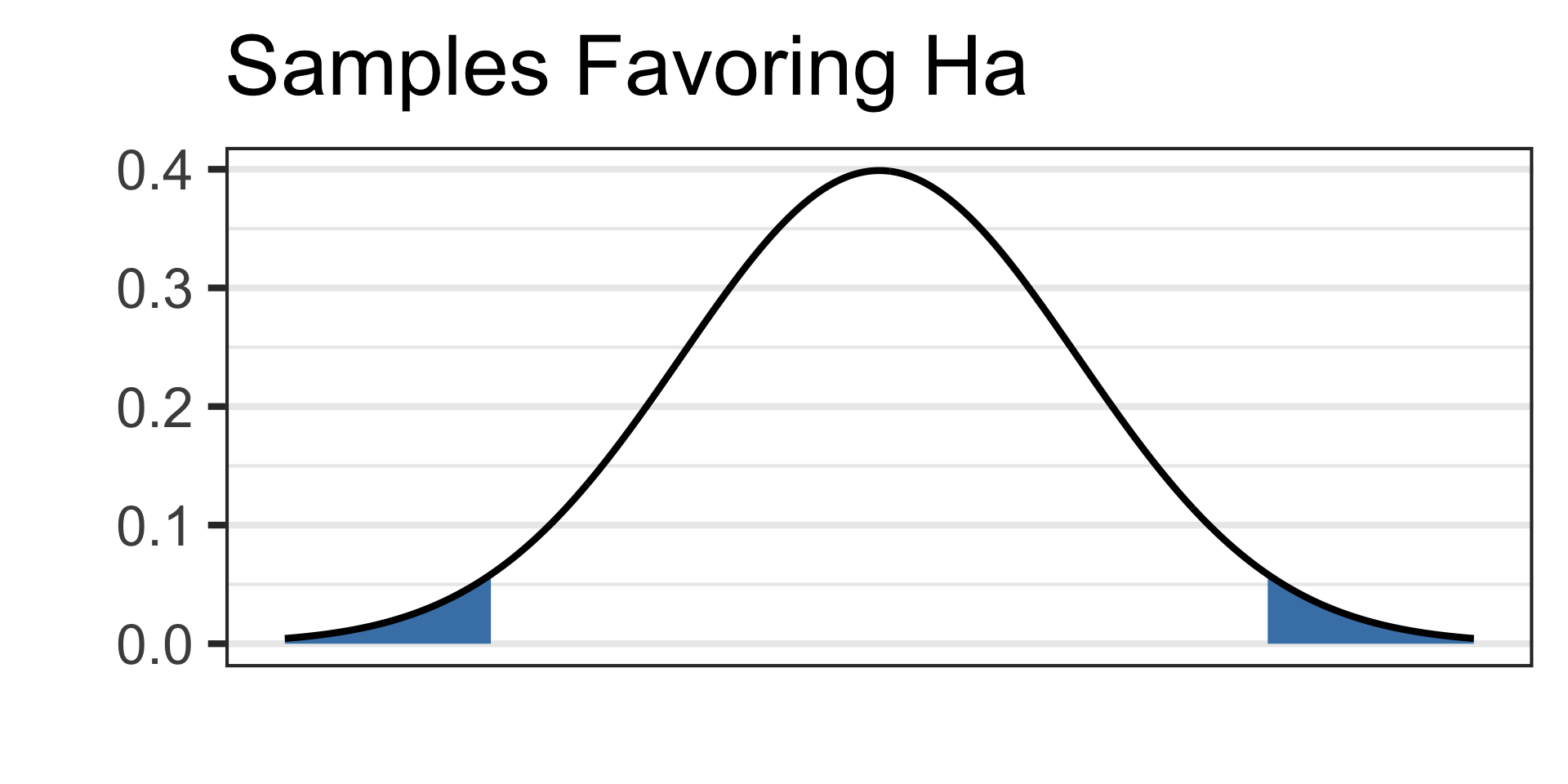
- Set \(\alpha = 0.10\)
- We’ll calculate the test statistic, where \(\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}\)
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
We’re testing a claim comparing two population
proportionsThe hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)See the picture of the alternative hypothesis below:
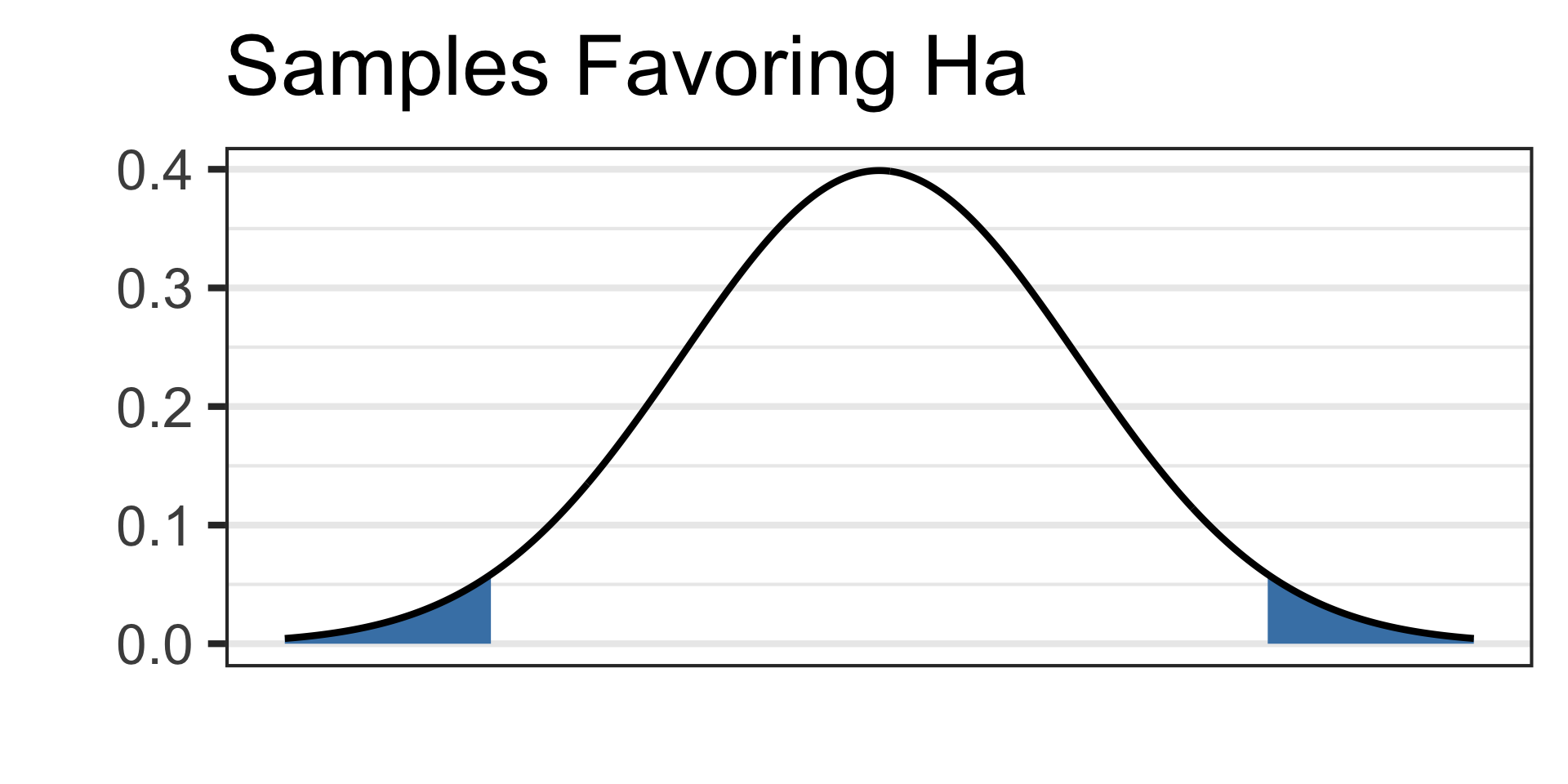
- Set \(\alpha = 0.10\)
- We’ll calculate the test statistic, where \(\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}\)
Notice that \(\displaystyle{p_{\text{swipe}} = \frac{46}{200}}\), so \(p_{\text{swipe}} = 0.23\) and
\(\displaystyle{p_{\text{personality}} = \frac{65}{180}}\), so \(p_{\text{personality}} \approx 0.3611\)
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
We’re testing a claim comparing two population
proportionsThe hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)See the picture of the alternative hypothesis below:
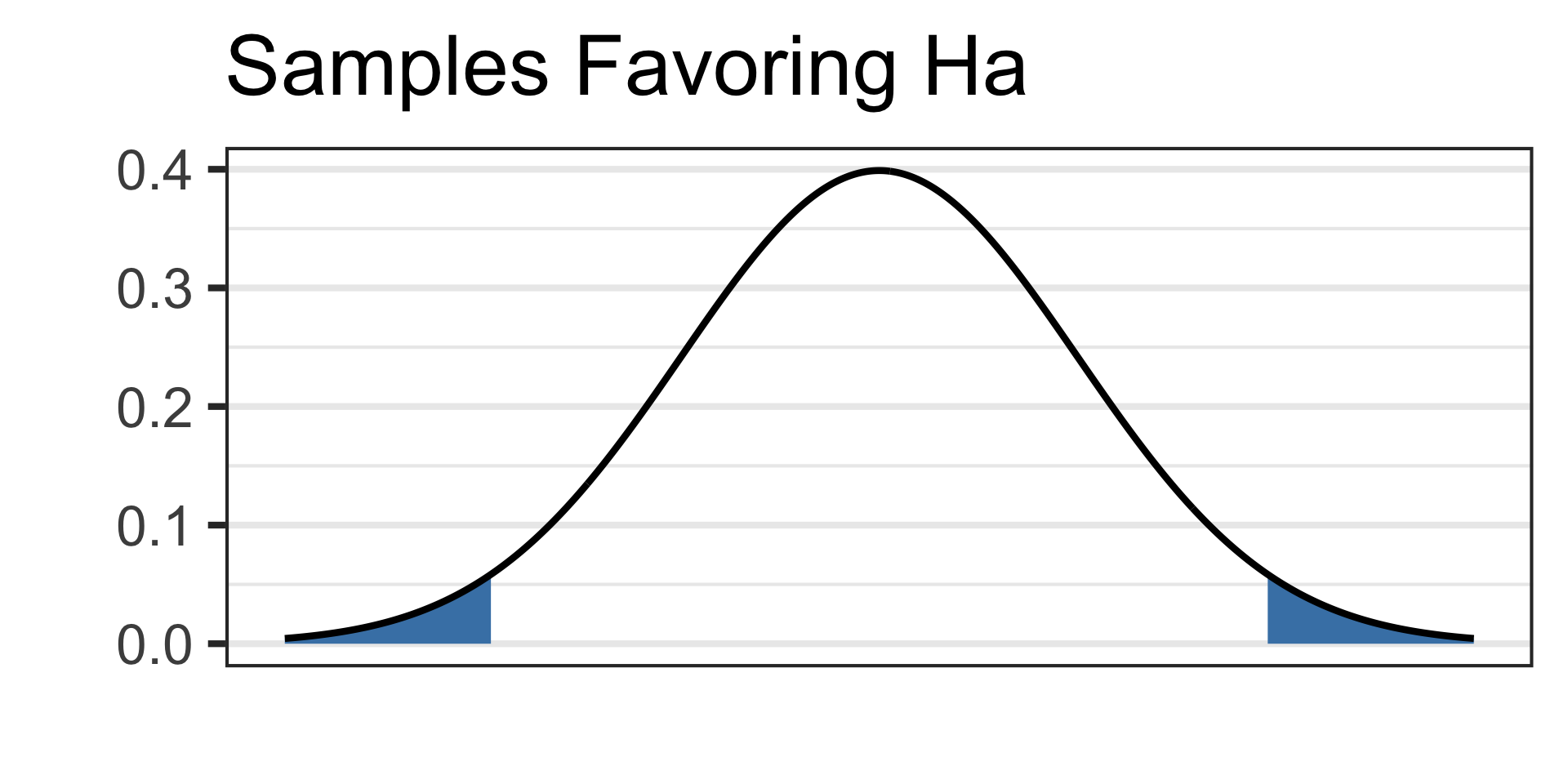
- Set \(\alpha = 0.10\)
- We’ll calculate the test statistic, where \(\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}\)
Notice that \(\displaystyle{p_{\text{swipe}} = \frac{46}{200}}\), so \(p_{\text{swipe}} = 0.23\) and
\(\displaystyle{p_{\text{personality}} = \frac{65}{180}}\), so \(p_{\text{personality}} \approx 0.3611\)
Notice also that our standard error is calculated as
\[S_E = \sqrt{\frac{p_{\text{swipe}}\left(1 - p_{\text{swipe}}\right)}{n_{\text{swipe}}} + \frac{p_{\text{personality}}\left(1 - p_{\text{personality}}\right)}{n_{\text{personality}}}}\]
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
We’re testing a claim comparing two population
proportionsThe hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)See the picture of the alternative hypothesis below:
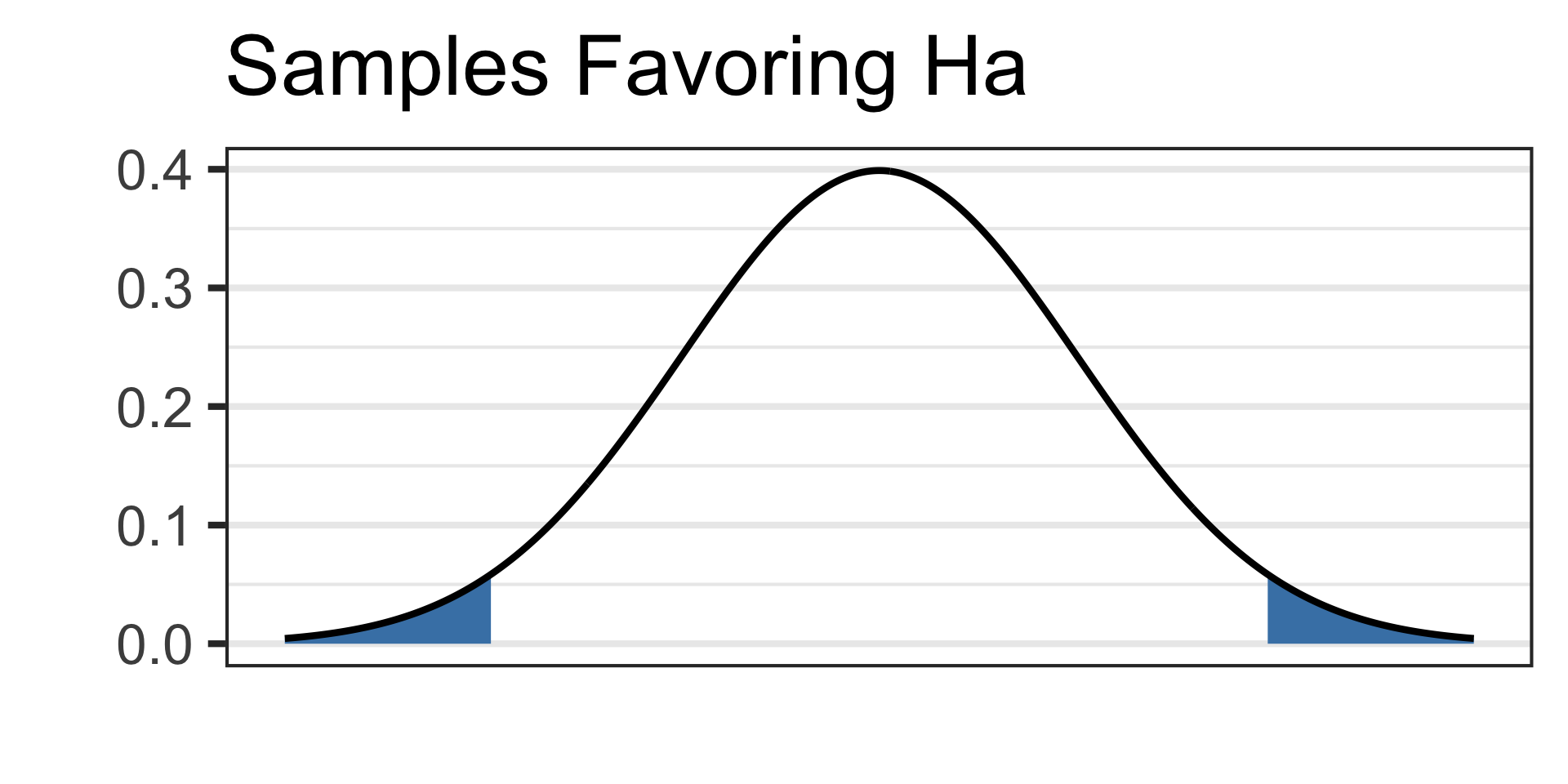
- Set \(\alpha = 0.10\)
- We’ll calculate the test statistic, where \(\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}\)
Notice that \(\displaystyle{p_{\text{swipe}} = \frac{46}{200}}\), so \(p_{\text{swipe}} = 0.23\) and
\(\displaystyle{p_{\text{personality}} = \frac{65}{180}}\), so \(p_{\text{personality}} \approx 0.3611\)
Notice also that our standard error is calculated as
\[S_E = \sqrt{\frac{p_{\text{swipe}}\left(1 - p_{\text{swipe}}\right)}{n_{\text{swipe}}} + \frac{p_{\text{personality}}\left(1 - p_{\text{personality}}\right)}{n_{\text{personality}}}}\]
So,
\[\texttt{test statistic} = \frac{\left(0.23 - 0.3611\right) - 0}{\sqrt{\frac{0.23\left(1 - 0.23\right)}{200} + \frac{0.3611\left(1 - 0.3611\right)}{180}}} \approx -2.82\]
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
We’re testing a claim comparing two population
proportionsThe hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)See the picture of the alternative hypothesis below:
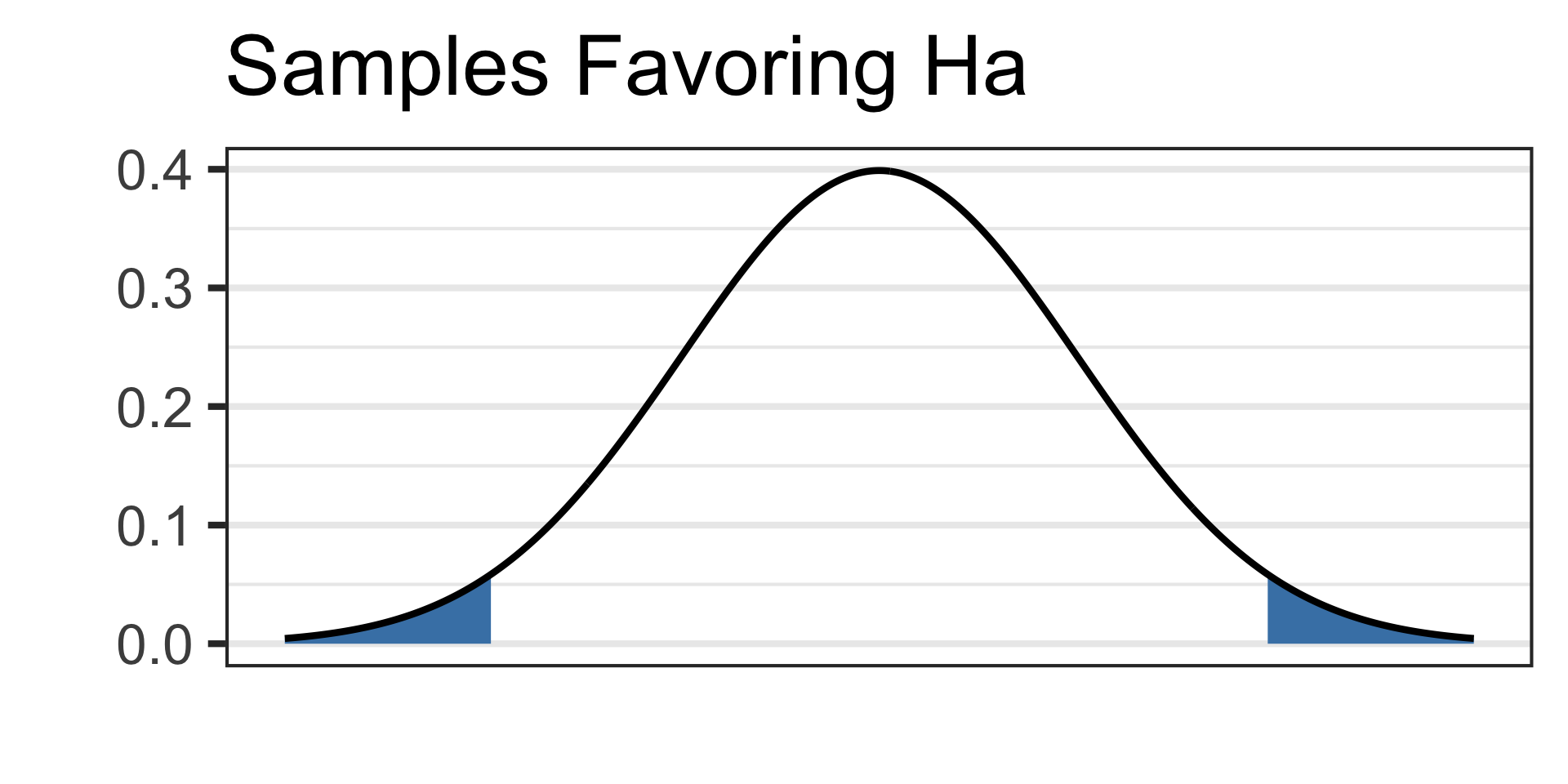
- Set \(\alpha = 0.10\)
- We’ll calculate the test statistic, where \(\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}\)
\[\texttt{test statistic} \approx -2.82\]
- Now we’ll draw our test statistic on our standard normal distribution and calculate the \(p\)-value
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
We’re testing a claim comparing two population
proportionsThe hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)See the picture of the alternative hypothesis below:
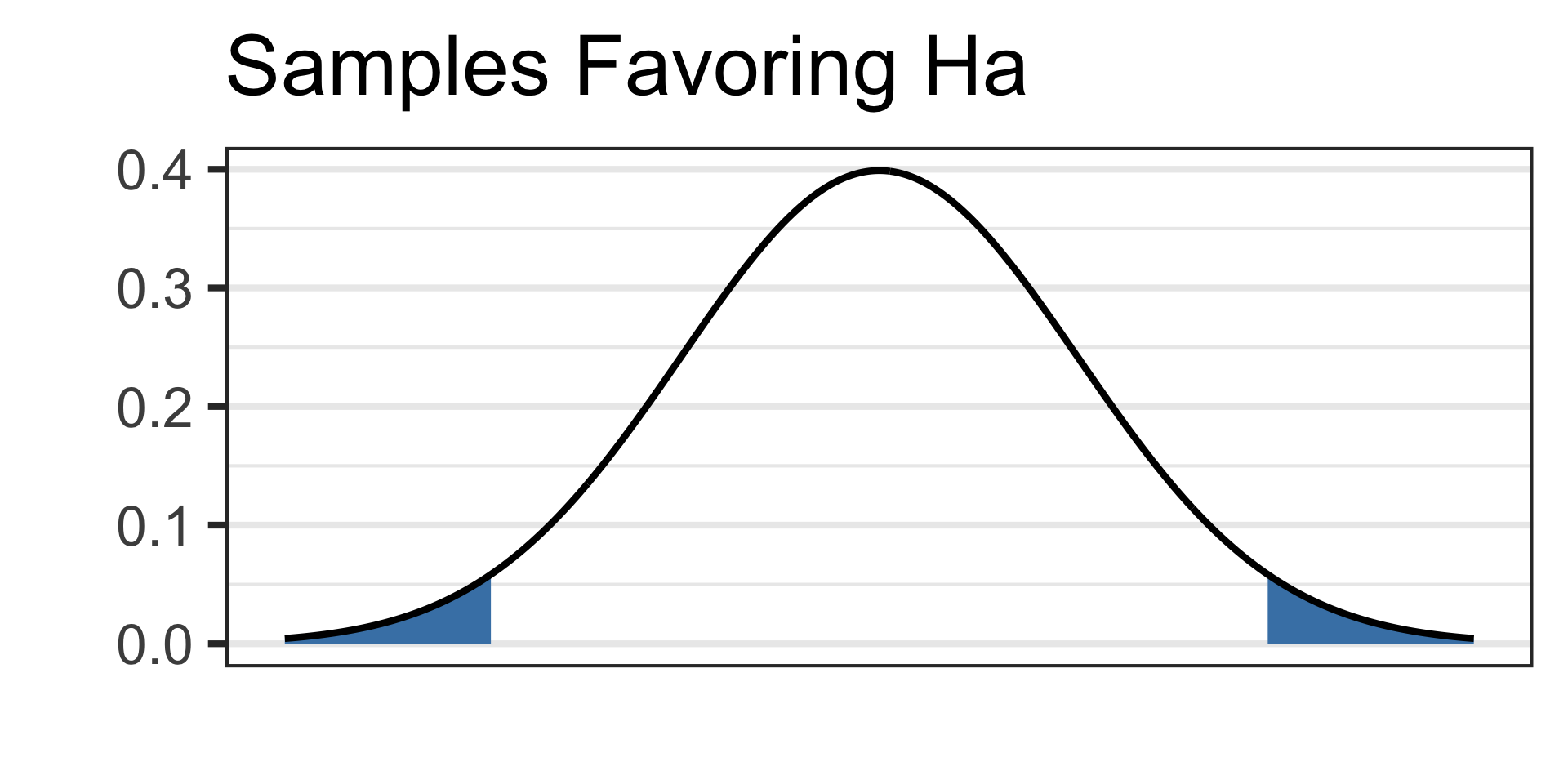
- Set \(\alpha = 0.10\)
- We’ll calculate the test statistic, where \(\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}\)
\[\texttt{test statistic} \approx -2.82\]
- Now we’ll draw our test statistic on our standard normal distribution and calculate the \(p\)-value
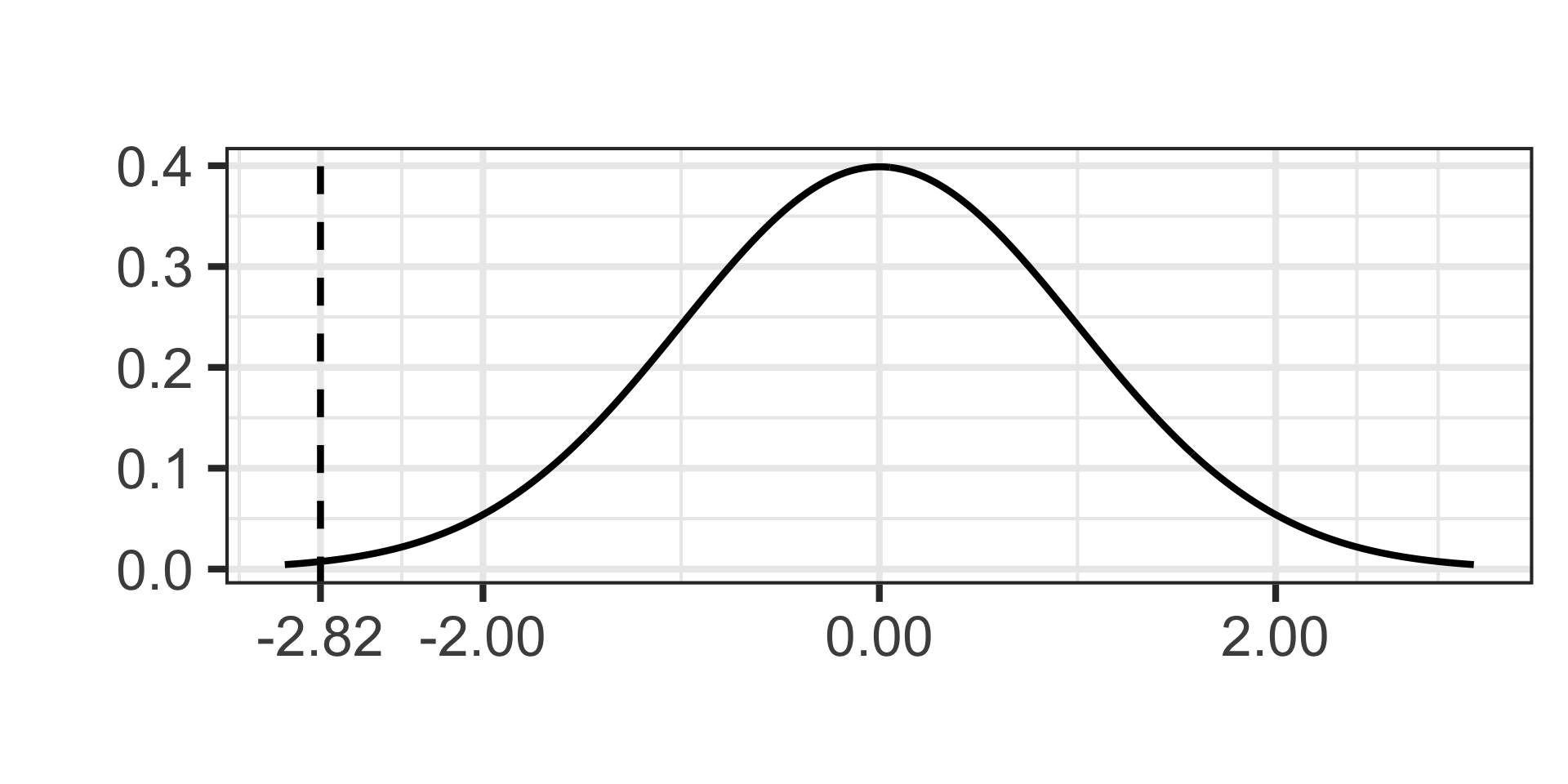
- \(p\)-value = …
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
We’re testing a claim comparing two population
proportionsThe hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)See the picture of the alternative hypothesis below:
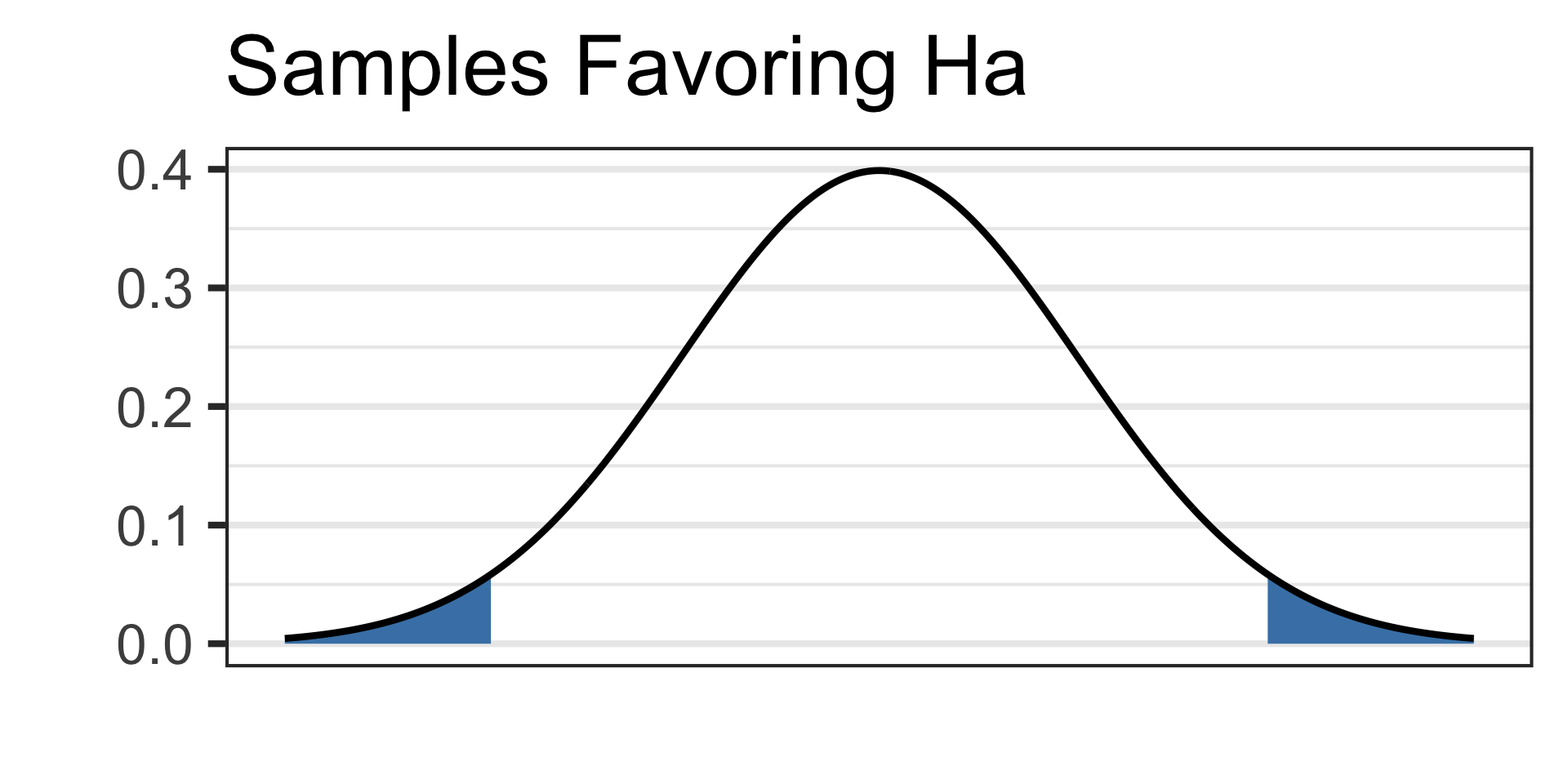
- Set \(\alpha = 0.10\)
- We’ll calculate the test statistic, where \(\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}\)
\[\texttt{test statistic} \approx -2.82\]
- Now we’ll draw our test statistic on our standard normal distribution and calculate the \(p\)-value
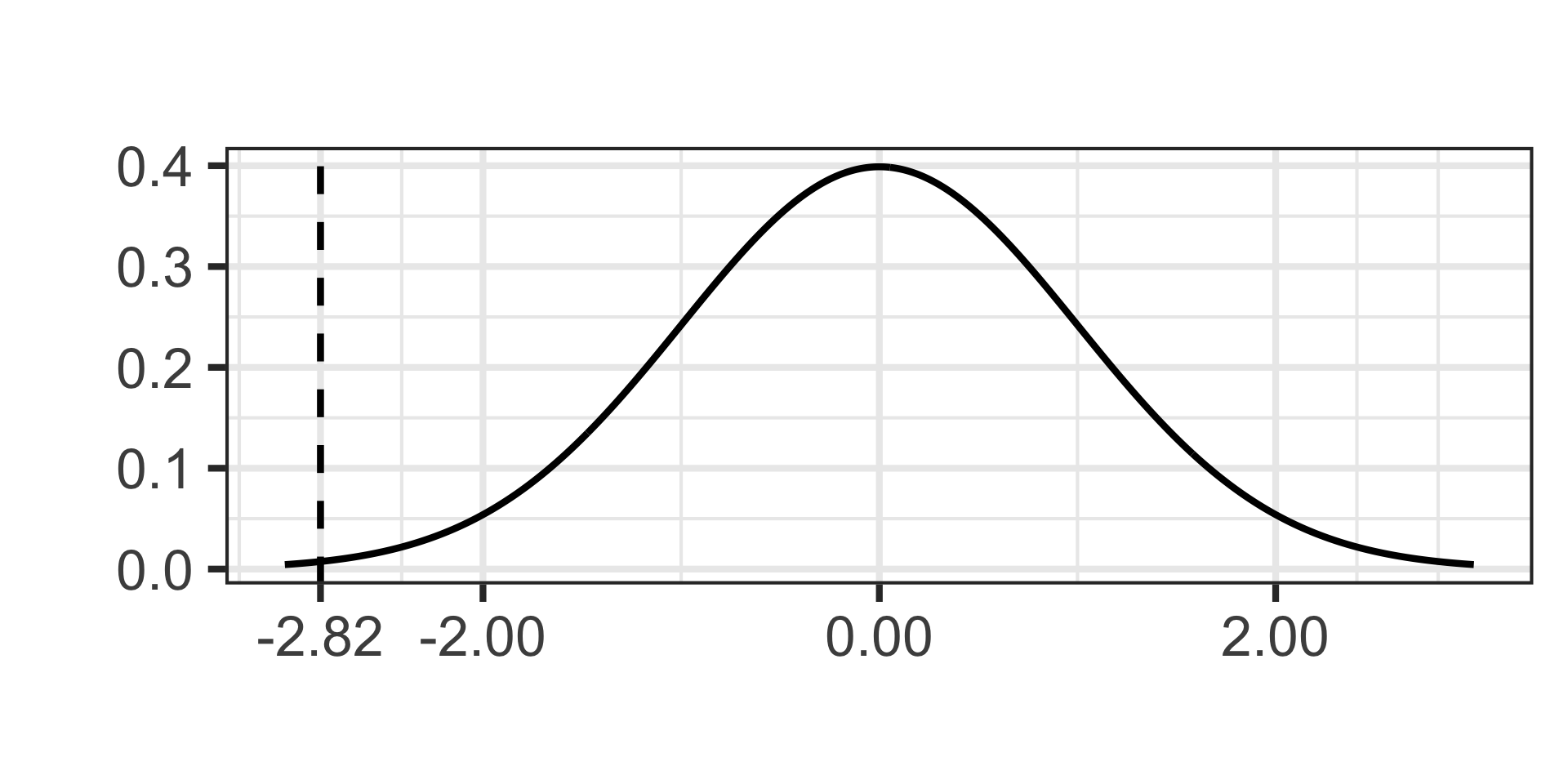
- \(p\)-value =
2*pnorm(-2.82, 0, 1)\(\approx\) 0.0048
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
We’re testing a claim comparing two population
proportionsThe hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)See the picture of the alternative hypothesis below:
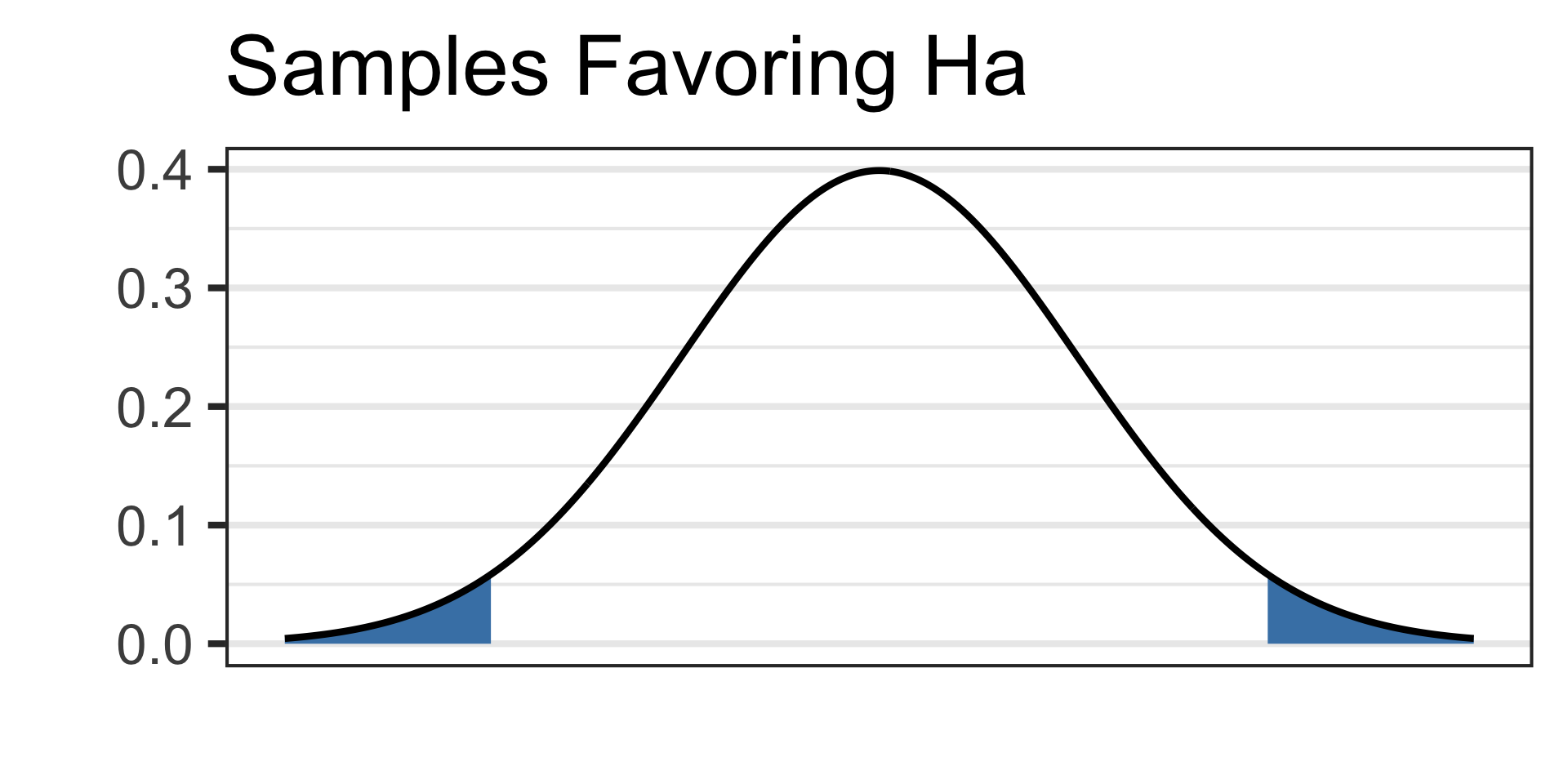
- Set \(\alpha = 0.10\)
- We’ll calculate the test statistic, where \(\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}\)
\[\texttt{test statistic} \approx -2.82\]
- Now we’ll draw our test statistic on our standard normal distribution and calculate the \(p\)-value
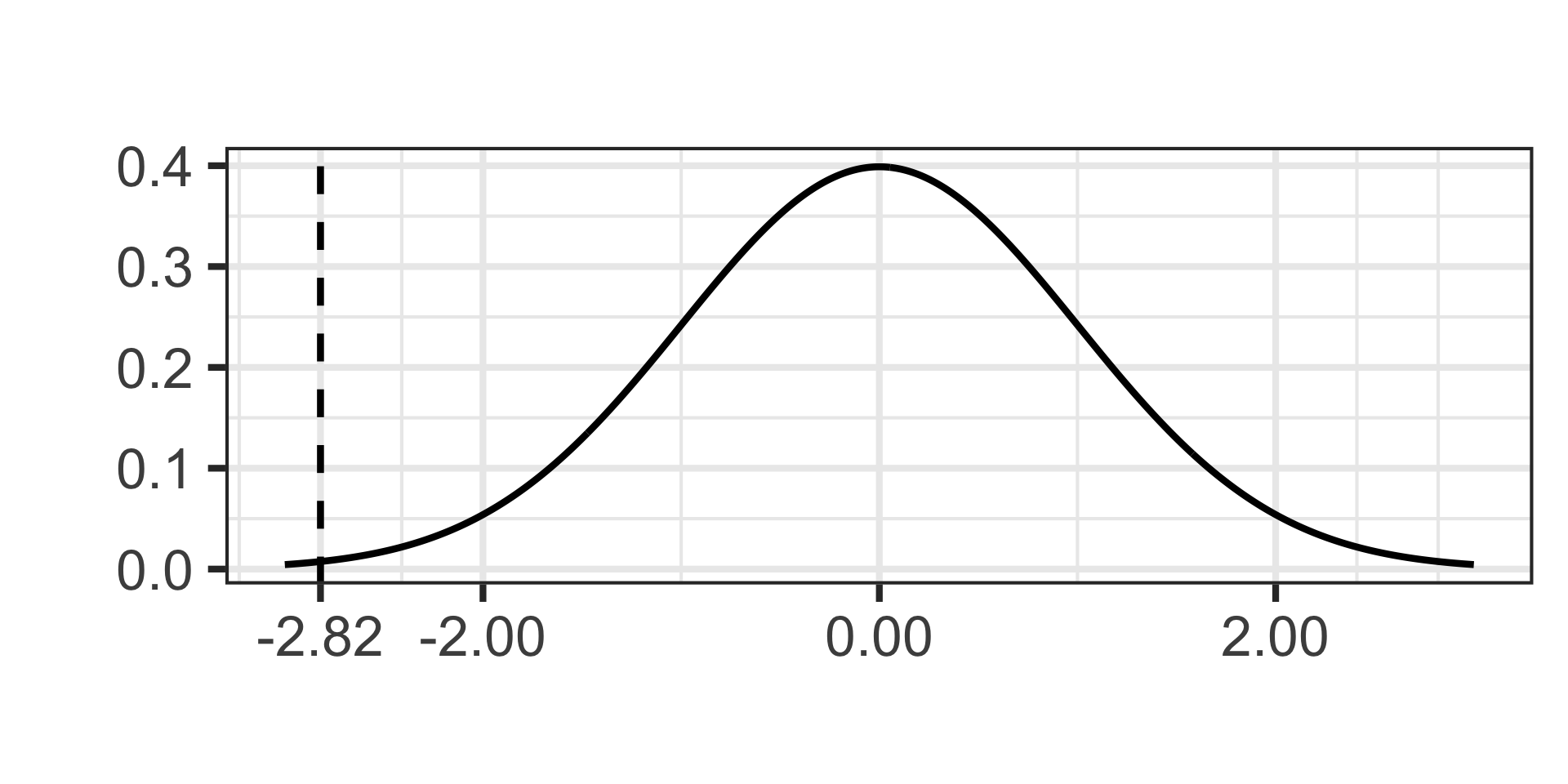
\(p\)-value =
2*pnorm(-2.82, 0, 1)\(\approx\) 0.0048\(p\)-value \(< \alpha\), we reject \(H_0\) and accept \(H_a\)
A Completed Hypothesis Test
Scenario: A group of students is curious about whether the success rates (finding a long-term relationship) differ between people using a swipe-based dating app versus a personality-based matchmaking app. They conduct a survey of users from both types of apps and compare the proportion of users who report being in a long-term relationship. On the swipe-based app, 46 out of 200 users surveyed reported being in a long-term relationship. On the personality-based site, 65 out of 180 users surveyed said the same. Is there significant evidence to suggest (at the 10% level of significance) that proportion of successful relationships are not the same for swipe-based apps and personality-based apps?
We’re testing a claim comparing two population
proportionsThe hypotheses are: \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} = p_{\text{personality}}\\ H_a & : & p_{\text{swipe}} \neq p_{\text{personality}}\end{array}\), but a
better way to write them is \(\begin{array}{lcl} H_0 & : & p_{\text{swipe}} - p_{\text{personality}} = 0\\ H_a & : & p_{\text{swipe}} - p_{\text{personality}} \neq 0\end{array}\)See the picture of the alternative hypothesis below:
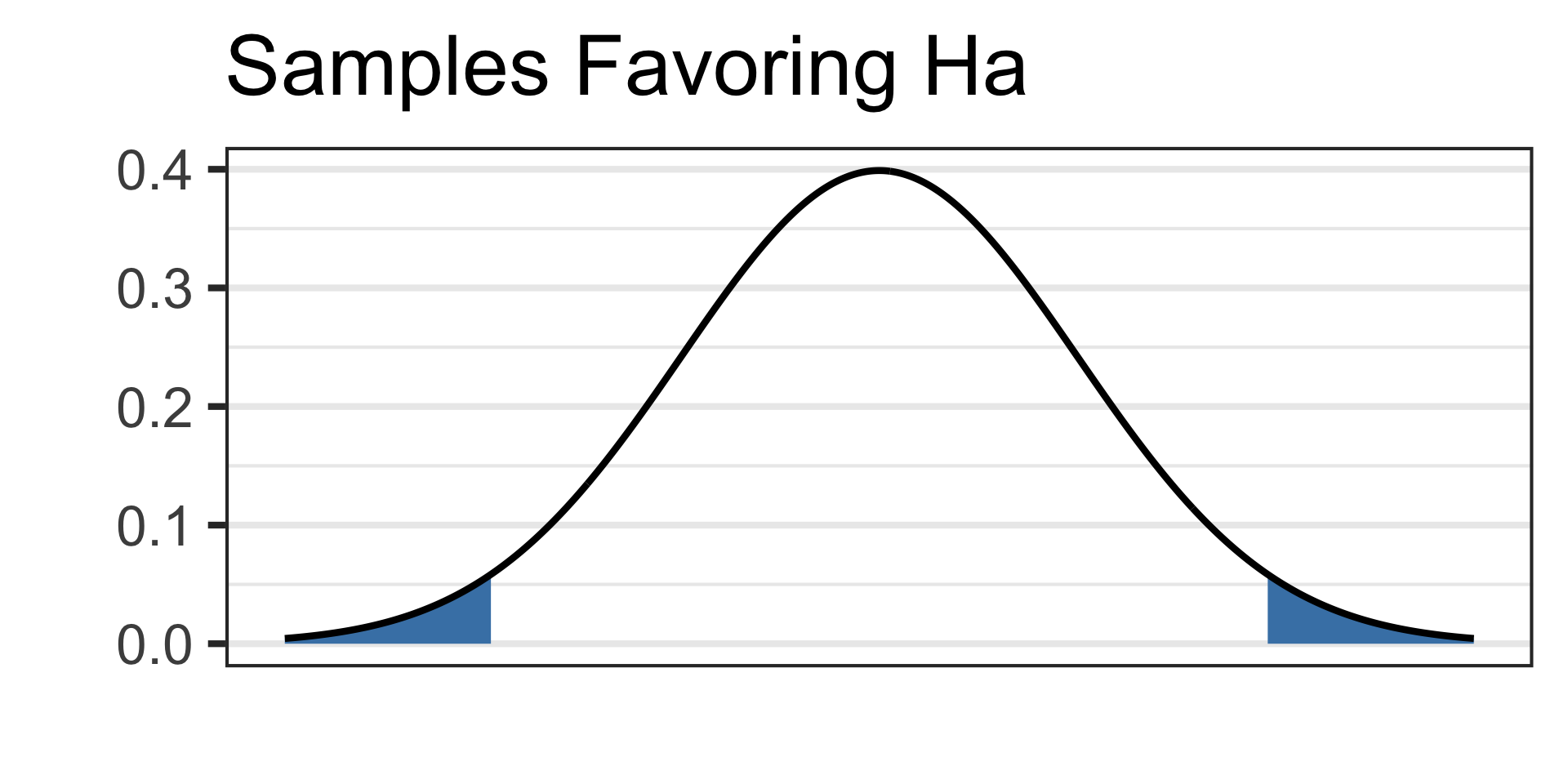
- Set \(\alpha = 0.10\)
- We’ll calculate the test statistic, where \(\texttt{test statistic} = \frac{\left(\texttt{point estimate}\right) - \left(\texttt{null value}\right)}{S_E}\)
\[\texttt{test statistic} \approx -2.82\]
- Now we’ll draw our test statistic on our standard normal distribution and calculate the \(p\)-value
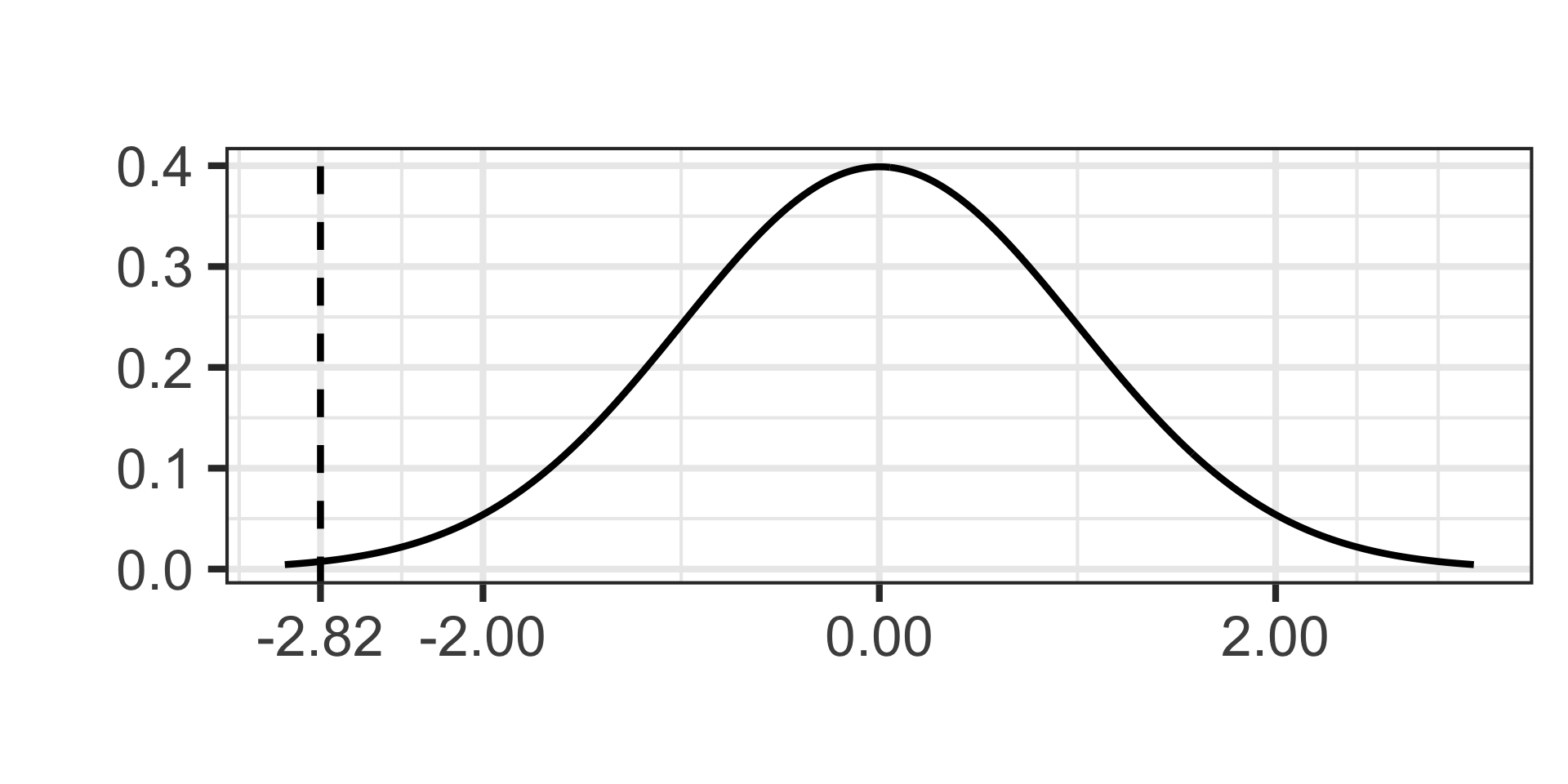
\(p\)-value =
2*pnorm(-2.82, 0, 1)\(\approx\) 0.0048Our observed data is incompatible with the proportion of successful relationships being equal. The relationship success rates differ across the two apps.
A Completed Confidence Interval
Scenario: A college wants to understand if there is a difference in the proportion of students who attend office hours in-person versus virtually. Faculty members noticed varying attendance patterns and want to explore whether virtual office hours increase engagement. Out of 120 students surveyed, 38 said that they attend in-person office hours regularly. A separate random sample of 140 students revealed that 62 attended virtual office hours regularly. Construct a 90% confidence interval for the difference in proportions of students attending virtual and face-to-face office hours regularly.
- Read the problem carefully \(\checkmark\)
- Estimate the difference between the proportions of students regularly attending virtual office hours versus in-person office hours
- The “formula” for the confidence
interval is
A Completed Confidence Interval
Scenario: A college wants to understand if there is a difference in the proportion of students who attend office hours in-person versus virtually. Faculty members noticed varying attendance patterns and want to explore whether virtual office hours increase engagement. Out of 120 students surveyed, 38 said that they attend in-person office hours regularly. A separate random sample of 140 students revealed that 62 attended virtual office hours regularly. Construct a 90% confidence interval for the difference in proportions of students attending virtual and face-to-face office hours regularly.
- Read the problem carefully \(\checkmark\)
- Estimate the difference between the proportions of students regularly attending virtual office hours versus in-person office hours
- The “formula” for the confidence
interval is
\[\scriptsize{\left(\begin{array}{c}\texttt{point}\\ \texttt{estimate}\end{array}\right) \pm \left(\begin{array}{c}\texttt{critical}\\ \texttt{value}\end{array}\right)\cdot \left(\begin{array}{c}\texttt{standard}\\ \texttt{error}\end{array}\right)}\]
- The point estimate is the difference in proportions…
A Completed Confidence Interval
Scenario: A college wants to understand if there is a difference in the proportion of students who attend office hours in-person versus virtually. Faculty members noticed varying attendance patterns and want to explore whether virtual office hours increase engagement. Out of 120 students surveyed, 38 said that they attend in-person office hours regularly. A separate random sample of 140 students revealed that 62 attended virtual office hours regularly. Construct a 90% confidence interval for the difference in proportions of students attending virtual and face-to-face office hours regularly.
- Read the problem carefully \(\checkmark\)
- Estimate the difference between the proportions of students regularly attending virtual office hours versus in-person office hours
- The “formula” for the confidence
interval is
\[\scriptsize{\left(\begin{array}{c}\texttt{point}\\ \texttt{estimate}\end{array}\right) \pm \left(\begin{array}{c}\texttt{critical}\\ \texttt{value}\end{array}\right)\cdot \left(\begin{array}{c}\texttt{standard}\\ \texttt{error}\end{array}\right)}\]
- The point estimate is the difference in proportions…
Notice that \(\displaystyle{p_{\text{virtual}} = \frac{62}{140}}\) and \(\displaystyle{p_{\text{in-person}} = \frac{38}{120}}\), so \(p_{\text{virtual}} \approx 0.4429\) and \(p_{\text{in-person}} \approx 0.3167\)
A Completed Confidence Interval
Scenario: A college wants to understand if there is a difference in the proportion of students who attend office hours in-person versus virtually. Faculty members noticed varying attendance patterns and want to explore whether virtual office hours increase engagement. Out of 120 students surveyed, 38 said that they attend in-person office hours regularly. A separate random sample of 140 students revealed that 62 attended virtual office hours regularly. Construct a 90% confidence interval for the difference in proportions of students attending virtual and face-to-face office hours regularly.
- Read the problem carefully \(\checkmark\)
- Estimate the difference between the proportions of students regularly attending virtual office hours versus in-person office hours
- The “formula” for the confidence
interval is
\[\scriptsize{\left(\begin{array}{c}\texttt{point}\\ \texttt{estimate}\end{array}\right) \pm \left(\begin{array}{c}\texttt{critical}\\ \texttt{value}\end{array}\right)\cdot \left(\begin{array}{c}\texttt{standard}\\ \texttt{error}\end{array}\right)}\]
- The point estimate is the difference in proportions…
Notice that \(\displaystyle{p_{\text{virtual}} = \frac{62}{140}}\) and \(\displaystyle{p_{\text{in-person}} = \frac{38}{120}}\), so \(p_{\text{virtual}} \approx 0.4429\) and \(p_{\text{in-person}} \approx 0.3167\)
The point estimate is
\[p_{\text{virtual}} - p_{\text{in-person}} \approx 0.1262\]
- The standard error is…
A Completed Confidence Interval
Scenario: A college wants to understand if there is a difference in the proportion of students who attend office hours in-person versus virtually. Faculty members noticed varying attendance patterns and want to explore whether virtual office hours increase engagement. Out of 120 students surveyed, 38 said that they attend in-person office hours regularly. A separate random sample of 140 students revealed that 62 attended virtual office hours regularly. Construct a 90% confidence interval for the difference in proportions of students attending virtual and face-to-face office hours regularly.
- Read the problem carefully \(\checkmark\)
- Estimate the difference between the proportions of students regularly attending virtual office hours versus in-person office hours
- The “formula” for the confidence
interval is
\[\scriptsize{\left(\begin{array}{c}\texttt{point}\\ \texttt{estimate}\end{array}\right) \pm \left(\begin{array}{c}\texttt{critical}\\ \texttt{value}\end{array}\right)\cdot \left(\begin{array}{c}\texttt{standard}\\ \texttt{error}\end{array}\right)}\]
- The point estimate is the difference in proportions…
Notice that \(\displaystyle{p_{\text{virtual}} = \frac{62}{140}}\) and \(\displaystyle{p_{\text{in-person}} = \frac{38}{120}}\), so \(p_{\text{virtual}} \approx 0.4429\) and \(p_{\text{in-person}} \approx 0.3167\)
The point estimate is
\[p_{\text{virtual}} - p_{\text{in-person}} \approx 0.1262\]
- The standard error is…
\[\begin{align*}S_E &= \sqrt{\frac{p_{\text{virtual}}\left(1 - p_{\text{virtual}}\right)}{n_{\text{virtual}}} + \frac{p_{\text{in-person}}\left(1 - p_{\text{in-person}}\right)}{n_{\text{in-person}}}}\end{align*}\]
A Completed Confidence Interval
Scenario: A college wants to understand if there is a difference in the proportion of students who attend office hours in-person versus virtually. Faculty members noticed varying attendance patterns and want to explore whether virtual office hours increase engagement. Out of 120 students surveyed, 38 said that they attend in-person office hours regularly. A separate random sample of 140 students revealed that 62 attended virtual office hours regularly. Construct a 90% confidence interval for the difference in proportions of students attending virtual and face-to-face office hours regularly.
- Read the problem carefully \(\checkmark\)
- Estimate the difference between the proportions of students regularly attending virtual office hours versus in-person office hours
- The “formula” for the confidence
interval is
\[\scriptsize{\left(\begin{array}{c}\texttt{point}\\ \texttt{estimate}\end{array}\right) \pm \left(\begin{array}{c}\texttt{critical}\\ \texttt{value}\end{array}\right)\cdot \left(\begin{array}{c}\texttt{standard}\\ \texttt{error}\end{array}\right)}\]
- The point estimate is the difference in proportions…
Notice that \(\displaystyle{p_{\text{virtual}} = \frac{62}{140}}\) and \(\displaystyle{p_{\text{in-person}} = \frac{38}{120}}\), so \(p_{\text{virtual}} \approx 0.4429\) and \(p_{\text{in-person}} \approx 0.3167\)
The point estimate is
\[p_{\text{virtual}} - p_{\text{in-person}} \approx 0.1262\]
- The standard error is…
\[\begin{align*} S_E &= \sqrt{\frac{p_{\text{virtual}}\left(1 - p_{\text{virtual}}\right)}{n_{\text{virtual}}} + \frac{p_{\text{in-person}}\left(1 - p_{\text{in-person}}\right)}{n_{\text{in-person}}}}\\ &\approx \sqrt{\frac{0.4429\left(1 - 0.4429\right)}{140} + \frac{0.3167\left(1 - 0.3167\right)}{120}}\end{align*}\]
A Completed Confidence Interval
Scenario: A college wants to understand if there is a difference in the proportion of students who attend office hours in-person versus virtually. Faculty members noticed varying attendance patterns and want to explore whether virtual office hours increase engagement. Out of 120 students surveyed, 38 said that they attend in-person office hours regularly. A separate random sample of 140 students revealed that 62 attended virtual office hours regularly. Construct a 90% confidence interval for the difference in proportions of students attending virtual and face-to-face office hours regularly.
- Read the problem carefully \(\checkmark\)
- Estimate the difference between the proportions of students regularly attending virtual office hours versus in-person office hours
- The “formula” for the confidence
interval is
\[\scriptsize{\left(\begin{array}{c}\texttt{point}\\ \texttt{estimate}\end{array}\right) \pm \left(\begin{array}{c}\texttt{critical}\\ \texttt{value}\end{array}\right)\cdot \left(\begin{array}{c}\texttt{standard}\\ \texttt{error}\end{array}\right)}\]
- The point estimate is the difference in proportions…
Notice that \(\displaystyle{p_{\text{virtual}} = \frac{62}{140}}\) and \(\displaystyle{p_{\text{in-person}} = \frac{38}{120}}\), so \(p_{\text{virtual}} \approx 0.4429\) and \(p_{\text{in-person}} \approx 0.3167\)
The point estimate is
\[p_{\text{virtual}} - p_{\text{in-person}} \approx 0.1262\]
- The standard error is…
\[\begin{align*} S_E &= \sqrt{\frac{p_{\text{virtual}}\left(1 - p_{\text{virtual}}\right)}{n_{\text{virtual}}} + \frac{p_{\text{in-person}}\left(1 - p_{\text{in-person}}\right)}{n_{\text{in-person}}}}\\ &\approx \sqrt{\frac{0.4429\left(1 - 0.4429\right)}{140} + \frac{0.3167\left(1 - 0.3167\right)}{120}}\\ &\approx \sqrt{0.00176 + 0.0018}\end{align*}\]
A Completed Confidence Interval
Scenario: A college wants to understand if there is a difference in the proportion of students who attend office hours in-person versus virtually. Faculty members noticed varying attendance patterns and want to explore whether virtual office hours increase engagement. Out of 120 students surveyed, 38 said that they attend in-person office hours regularly. A separate random sample of 140 students revealed that 62 attended virtual office hours regularly. Construct a 90% confidence interval for the difference in proportions of students attending virtual and face-to-face office hours regularly.
- Read the problem carefully \(\checkmark\)
- Estimate the difference between the proportions of students regularly attending virtual office hours versus in-person office hours
- The “formula” for the confidence
interval is
\[\scriptsize{\left(\begin{array}{c}\texttt{point}\\ \texttt{estimate}\end{array}\right) \pm \left(\begin{array}{c}\texttt{critical}\\ \texttt{value}\end{array}\right)\cdot \left(\begin{array}{c}\texttt{standard}\\ \texttt{error}\end{array}\right)}\]
- The point estimate is the difference in proportions…
Notice that \(\displaystyle{p_{\text{virtual}} = \frac{62}{140}}\) and \(\displaystyle{p_{\text{in-person}} = \frac{38}{120}}\), so \(p_{\text{virtual}} \approx 0.4429\) and \(p_{\text{in-person}} \approx 0.3167\)
The point estimate is
\[p_{\text{virtual}} - p_{\text{in-person}} \approx 0.1262\]
- The standard error is…
\[\begin{align*} S_E &= \sqrt{\frac{p_{\text{virtual}}\left(1 - p_{\text{virtual}}\right)}{n_{\text{virtual}}} + \frac{p_{\text{in-person}}\left(1 - p_{\text{in-person}}\right)}{n_{\text{in-person}}}}\\ &\approx \sqrt{\frac{0.4429\left(1 - 0.4429\right)}{140} + \frac{0.3167\left(1 - 0.3167\right)}{120}}\\ &\approx \sqrt{0.00176 + 0.0018}\\ &\approx 0.0597\end{align*}\]
The critical value is \(\displaystyle{z_{\alpha/2} = 1.65}\)
The confidence bounds are \(\displaystyle{0.1262 \pm 1.65\left(0.0597\right) \to \left\{\begin{array}{lcl} 0.1262 + 0.0985 & = & 0.2247\\ 0.1262 - 0.0985 & = & 0.0277\end{array}\right.}\)
We are 90% confident that the true difference in proportions of students regularly attending virtual office hours versus in person office hours is somewhere between 2.77% and 22.47%, with virtual office hour attendance being more prevalent.
Examples to Try
The following slides contain several examples to try
There are more than we’ll be able to complete during this class meeting
The examples include a mixture of scenarios involving single population proportion or comparison between two population proportions
The examples also include a mixture of questions which are best answered with confidence intervals or best answered with hypothesis tests
Examples to Try: Streaming Subscription Rates
Scenario: A streaming service wants to estimate the proportion of its users who would be interested in subscribing to a premium plan without ads. Out of a random sample of 450 users surveyed, 135 reported being interested in such a subscription. Construct a 95% confidence interval for the population proportion of users who would be interested in this subscription.
Examples to Try: Satisfactory Work-Life Balance
Scenario: A company is interested in comparing the proportion of employees who report satisfaction with their work-life balance between remote workers and those who work in the office. Out of 200 remote workers, 160 are satisfied, while out of 220 in-office workers, 154 are satisfied. Does this data provide evidence to suggest that remote workers are more satisfied with their work-life balance than their in-office counterparts on average?
Examples to Try: Autonomous Drone Deliveries
Scenario: A city planning board is considering proposals to reduce roadway impedances due to temporarily parked delivery vehicles. They received a proposal on piloting an autonomous drone package delivery system from the company making the vast majority of deliveries within their city. The board is trying to gauge public acceptance of autonomous delivery drones. They ask you to determine whether a majority of residents support such an initiative. The board has already surveyed 1000 random residents and 597 were supportive of the delivery drone proposal.
Examples to Try: College Athletes and Vegan Diets
Scenario: A university athletic department is curious whether the proportion of athletes who follow a vegan diet is different between male and female athletes. Out of 176 randomly sampled male athletes, 12 followed a vegan diet while out of 153 female athletes, 28 follow a vegan diet. Do these samples provide evidence to suggest that the proportion of male and female athletes choosing a vegan diet differ?
Examples to Try: Working in Your Field
Scenario: A college career services department wants to compare the proportion of new graduates working in their field of study between those who completed internships and those who did not. Out of 150 randomly selected students who completed internships, 110 are working in their field. Similarly, out of 130 students without internships, 82 are working in their field. Construct a 90% confidence interval for the difference in proportions of recent graduates working in their field for those who completed an internship versus those who did not.
Examples to Try: Getting News from Social Media
Scenario: Researchers want to estimate the proportion of college students who use social media as their primary source of political news to see if it exceeds 70%. Out of 320 randomly selected students, 246 said they use social media as their primary source for political news. Does this sample suggest that the proportion of college students using social media as their primary news source exceeds 70% at the \(\alpha = 0.10\) level of significance?
Examples to Try: Mobile Voting Apps
Scenario: A local government is considering adopting a mobile app for voting and wants to estimate the proportion of residents in favor of the initiative. Out of 500 residents surveyed, 127 expressed support for a mobile voting app. Construct a 99% confidence interval for the proportion of residents in favor of a mobile voting app.
Examples to Try: Support for a New Environmental Policy
Scenario: A politician claims that a minority of the public supports a new environmental policy. A random sample of 900 people finds that 54% of them support the policy. At the 5% significance level, can you reject the politician’s claim?
Next Time…
Categorical Inference Lab