Analysis of Variance (ANOVA) and Linear Regression

Dr. Gilbert

December 9, 2024

The Highlights

What’s left in our inference journey?
A reminder of the Ames home sales data
ANOVA – testing for a difference in means across multiple (more than two) groups
- Some intuition for ANOVA
- The mechanics of ANOVA
- A completed example using home sales in Ames, IA
- Limits to ANOVA Results, and Post-Hoc (Follow-Up) Tests
What’s still left in our inference journey?
A reminder on linear functions: $y = mx + b$ and $\mathbb{E}\left[y\right] = \beta_0 + \beta_1\cdot x$
Linear Regression
- Simple Linear Regression
- Multiple Linear Regression
Summary and Closing

What’s Left for Inference?

Inference On...	"Test" Name
One Binary Categorical Variable	One Sample z
Association Between Two Binary Categorical Variables	Two Sample z
One MultiClass Categorical Variable	Chi-Squared GOF
Associations Between Two MultiClass Categorical Variables	Chi-Squared Independence
One Numerical Variable	One Sample t
Association Between a Numerical Variable and a Binary Categorical Variable	Two Sample t
Association Between a Numerical Variable and a MultiClass Categorical Variable	?
Association Between a Numerical Variable and a Single Other Numerical Variable	?
Association Between a Numerical Variable and Many Other Variables	?
Association Between a Categorical Variable and Many Other Variables	✘ (MAT434)

The `ames` Home Sales Data

The ames data set includes data on houses sold in Ames, IA between 2006 and 2010

The dataset includes 82 features of 2,930 sold homes – that is, the dataset includes 82 variables and 2,930 observations

Order	PID	area	price	MS.SubClass	MS.Zoning	Lot.Frontage	Lot.Area	Street	Alley	Lot.Shape	Land.Contour	Utilities	Lot.Config	Land.Slope	Neighborhood	Condition.1	Condition.2	Bldg.Type	House.Style	Overall.Qual	Overall.Cond	Year.Built	Year.Remod.Add	Roof.Style	Roof.Matl	Exterior.1st	Exterior.2nd	Mas.Vnr.Type	Mas.Vnr.Area	Exter.Qual	Exter.Cond	Foundation	Bsmt.Qual	Bsmt.Cond	Bsmt.Exposure	BsmtFin.Type.1	BsmtFin.SF.1	BsmtFin.Type.2	BsmtFin.SF.2	Bsmt.Unf.SF	Total.Bsmt.SF	Heating	Heating.QC	Central.Air	Electrical	X1st.Flr.SF	X2nd.Flr.SF	Bsmt.Full.Bath	Full.Bath	Half.Bath	Bedroom.AbvGr	Kitchen.AbvGr	Kitchen.Qual	TotRms.AbvGrd	Functional	Fireplaces	Fireplace.Qu	Garage.Type	Garage.Yr.Blt	Garage.Finish	Garage.Cars	Garage.Area	Garage.Qual	Garage.Cond	Paved.Drive	Wood.Deck.SF	Open.Porch.SF	Screen.Porch	Pool.QC	Fence	Misc.Feature	Misc.Val	Mo.Sold	Yr.Sold	Sale.Type	Sale.Condition
1	526301100	1656	215000	20	RL	141	31770	Pave	NA	IR1	Lvl	AllPub	Corner	Gtl	NAmes	Norm	Norm	1Fam	1Story	6	5	1960	1960	Hip	CompShg	BrkFace	Plywood	Stone	112	TA	TA	CBlock	TA	Gd	Gd	BLQ	639	Unf	0	441	1080	GasA	Fa	Y	SBrkr	1656	0	1	1	0	3	1	TA	7	Typ	2	Gd	Attchd	1960	Fin	2	528	TA	TA	P	210	62	0	NA	NA	NA	0	5	2010	WD	Normal
2	526350040	896	105000	20	RH	80	11622	Pave	NA	Reg	Lvl	AllPub	Inside	Gtl	NAmes	Feedr	Norm	1Fam	1Story	5	6	1961	1961	Gable	CompShg	VinylSd	VinylSd	None	0	TA	TA	CBlock	TA	TA	No	Rec	468	LwQ	144	270	882	GasA	TA	Y	SBrkr	896	0	0	1	0	2	1	TA	5	Typ	0	NA	Attchd	1961	Unf	1	730	TA	TA	Y	140	0	120	NA	MnPrv	NA	0	6	2010	WD	Normal
3	526351010	1329	172000	20	RL	81	14267	Pave	NA	IR1	Lvl	AllPub	Corner	Gtl	NAmes	Norm	Norm	1Fam	1Story	6	6	1958	1958	Hip	CompShg	Wd Sdng	Wd Sdng	BrkFace	108	TA	TA	CBlock	TA	TA	No	ALQ	923	Unf	0	406	1329	GasA	TA	Y	SBrkr	1329	0	0	1	1	3	1	Gd	6	Typ	0	NA	Attchd	1958	Unf	1	312	TA	TA	Y	393	36	0	NA	NA	Gar2	12500	6	2010	WD	Normal
4	526353030	2110	244000	20	RL	93	11160	Pave	NA	Reg	Lvl	AllPub	Corner	Gtl	NAmes	Norm	Norm	1Fam	1Story	7	5	1968	1968	Hip	CompShg	BrkFace	BrkFace	None	0	Gd	TA	CBlock	TA	TA	No	ALQ	1065	Unf	0	1045	2110	GasA	Ex	Y	SBrkr	2110	0	1	2	1	3	1	Ex	8	Typ	2	TA	Attchd	1968	Fin	2	522	TA	TA	Y	0	0	0	NA	NA	NA	0	4	2010	WD	Normal
5	527105010	1629	189900	60	RL	74	13830	Pave	NA	IR1	Lvl	AllPub	Inside	Gtl	Gilbert	Norm	Norm	1Fam	2Story	5	5	1997	1998	Gable	CompShg	VinylSd	VinylSd	None	0	TA	TA	PConc	Gd	TA	No	GLQ	791	Unf	0	137	928	GasA	Gd	Y	SBrkr	928	701	0	2	1	3	1	TA	6	Typ	1	TA	Attchd	1997	Fin	2	482	TA	TA	Y	212	34	0	NA	MnPrv	NA	0	3	2010	WD	Normal
6	527105030	1604	195500	60	RL	78	9978	Pave	NA	IR1	Lvl	AllPub	Inside	Gtl	Gilbert	Norm	Norm	1Fam	2Story	6	6	1998	1998	Gable	CompShg	VinylSd	VinylSd	BrkFace	20	TA	TA	PConc	TA	TA	No	GLQ	602	Unf	0	324	926	GasA	Ex	Y	SBrkr	926	678	0	2	1	3	1	Gd	7	Typ	1	Gd	Attchd	1998	Fin	2	470	TA	TA	Y	360	36	0	NA	NA	NA	0	6	2010	WD	Normal

I’ve reduced the data set to only include the four neighborhoods where the most properties were sold

The reduced data is stored in ames_small, which still has 82 features but only 1,143 records

Analysis of Variance (ANOVA)

Inferential Question: Does the average selling price of a home vary by neighborhood in Ames, IA?

Let’s start by identifying how many distinct neighborhoods are in ames_small

Neighborhood	n
NAmes	443
CollgCr	267
OldTown	239
Edwards	194

Analysis of Variance (ANOVA)

Inferential Question: Does the average selling price of a home vary by neighborhood in Ames, IA?

Let’s start by identifying how many distinct neighborhoods are in ames_small

Neighborhood	n
NAmes	443
CollgCr	267
OldTown	239
Edwards	194

There are four neighborhoods here! Our previous tests could only handle comparisons across two groups.

Analysis of Variance (ANOVA)

Inferential Question: Does the average selling price of a home vary by neighborhood in Ames, IA?

Let’s start by identifying how many distinct neighborhoods are in ames_small

Neighborhood	n
NAmes	443
CollgCr	267
OldTown	239
Edwards	194

There are four neighborhoods here! Our previous tests could only handle comparisons across two groups.

Analysis of Variance (ANOVA) provides a method for comparing group means across three or more groups

Analysis of Variance (ANOVA)

Inferential Question: Does the average selling price of a home vary by neighborhood in Ames, IA?

Let’s start by identifying how many distinct neighborhoods are in ames_small

Neighborhood	n
NAmes	443
CollgCr	267
OldTown	239
Edwards	194

There are four neighborhoods here! Our previous tests could only handle comparisons across two groups.

Analysis of Variance (ANOVA) provides a method for comparing group means across three or more groups

The hypotheses for an ANOVA test are:

\[\begin{array}{lcl} H_0 & : & \mu_1 = \mu_2 = \cdots = \mu_k~~\text{(All group means are equal)}\\ H_a & : & \text{At least one of the group means is different}\end{array}\]

Intuition for ANOVA

The main ideas behind ANOVA are somewhat simple…

Ignore the groups and calculate the variability from the overall mean
Calculate the variability from the group means
Calculate how much of the total variability is explained by differences between the group means ($\text{SS}_{\text{Total}} = \text{SS}_{\text{Between}} + \text{SS}_{\text{Within}}$)
Standardize the variability measures by turning them into averages
Compare the average between group variability to the average within group variability
- If the between and within group variability are similar, then there is no evidence that group means differ
- If the between and within group variability differ, then that is evidence that the group means differ from one another

Mechanics of ANOVA

Here are the main steps in an ANOVA test

Calculate the overall mean ($\bar{x}$) of all the observed data, ignoring the groups.
Compute the total sum of squares ($\text{SS}_{\text{Total}}$) to measure the overall variability in the data: $\text{SS}_\text{Total} = \sum (x - \bar{x})^2$
For each group, calculate the mean ($\bar{x}_i$) and the within-group sum of squares $\left(\text{SS}_{\text{Within}}\right)$, which measures the variability within each group: $\displaystyle{\text{SS}_\text{Within} = \sum_{\left(\text{groups, } i\right)} \sum_{\left(\text{observations, } x\right)} (x - \bar{x}_i)^2}$
Subtract the within-group variability from the total variability to get the between-group sum of squares ($\text{SS}_{\text{Between}}$), which measures how much the group means differ: $\text{SS}_\text{Between} = \text{SS}_\text{Total} - \text{SS}_\text{Within}$
Compute the mean squares:
- Mean Square Between ($\text{MS}_{\text{Between}} = \text{SS}_{\text{Between}} / \left(\text{num_groups} - 1\right)$)
- Mean Square Within ($\text{MS}_{\text{Within}} = \text{SS}_{\text{Within}} / \left(\text{num_observations} - \text{num_groups}\right)$)
The F-statistic is the ratio of these mean squares: $\displaystyle{F = \frac{\text{MS}_\text{Between}}{\text{MS}_\text{Within}}}$

Mechanics of ANOVA

Here are the main steps in an ANOVA test

Subtract the within-group variability from the total variability to get the between-group sum of squares ($\text{SS}_{\text{Between}}$), which measures how much the group means differ: $\text{SS}_\text{Between} = \text{SS}_\text{Total} - \text{SS}_\text{Within}$
Compute the mean squares:
- Mean Square Between ($\text{MS}_{\text{Between}} = \text{SS}_{\text{Between}} / \left(\text{num_groups} - 1\right)$)
- Mean Square Within ($\text{MS}_{\text{Within}} = \text{SS}_{\text{Within}} / \left(\text{num_observations} - \text{num_groups}\right)$)
The F-statistic is the ratio of these mean squares: $\displaystyle{F = \frac{\text{MS}_\text{Between}}{\text{MS}_\text{Within}}}$

Calculate the $p$-value using the $F$ distribution with df1 as “one less than the number of groups” ($k - 1$) and df2 as “the number of observations minus the number of groups” ($n - k$)
Interpret the results of the test as usual (and in context)

In Practice: The full ANOVA test will be run using software and we’ll just need to interpret the results

Completed Example: Home Sales by Neighborhood

Inferential Question: Do selling prices of homes vary by neighborhood in Ames?

\[\begin{array}{lcl} H_0 & : & \text{Average selling prices are the same across neighborhoods}\\ H_a & : & \text{At least one neighborhood has a difference average selling price}\end{array}\]

Let’s run the test:

ANOVA_results <- aov(price ~ Neighborhood, data = ames_small)
ANOVA_results %>%
  tidy()

term	df	sumsq	meansq	statistic	p.value
Neighborhood	3	9.574158e+11	319138602754	169.6027	6.888139e-91
Residuals	1139	2.143238e+12	1881683695	NA	NA

Result: The $p$-value is very small (it’s being rounded to 0 here). Since the $p$-value is less than $\alpha$ (0.05), we reject the null hypothesis and accept the alternative to it.

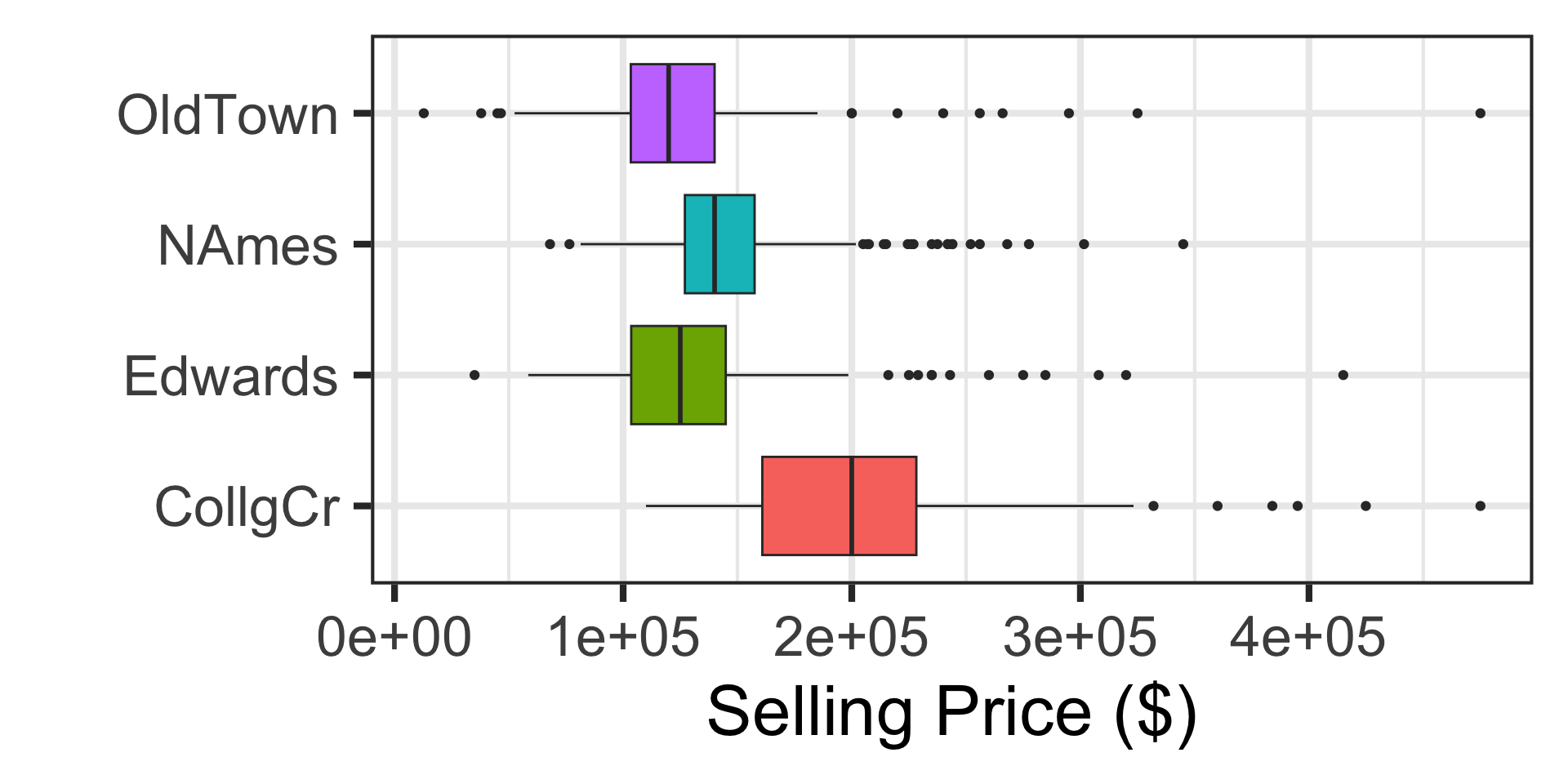
Result in Context: The average selling price of a home in Ames, IA does vary by neighborhood. At least one of the neighborhoods has a different average selling price than the others.

A Note on ANOVA Results

Notice that the result of the ANOVA test is simply that at least one neighborhood has a different average selling price

We don’t know which one, however

We can identify which neighborhood(s) differ from one another by either (i) using Tukey’s Honestly Significantly Different test, TukeyHSD() or (ii) using inference() to run the ANOVA test instead of aov()

A Note on ANOVA Results

To Use TukeyHSD(): Run the ANOVA test as we did previously and then

TukeyHSD(ANOVA_results)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = price ~ Neighborhood, data = ames_small)

$Neighborhood
                     diff        lwr        upr     p adj
Edwards-CollgCr -70960.05 -81488.832 -60431.274 0.0000000
NAmes-CollgCr   -56706.08 -65352.891 -48059.278 0.0000000
OldTown-CollgCr -77811.54 -87749.674 -67873.412 0.0000000
NAmes-Edwards    14253.97   4645.569  23862.368 0.0008200
OldTown-Edwards  -6851.49 -17636.690   3933.709 0.3596082
OldTown-NAmes   -21105.46 -30062.724 -12148.194 0.0000000

It looks like the data provides evidence suggesting that all pairs of neighborhoods have average selling prices that differ, except for the Old Town and Edwards neighborhoods which may have the same average selling price

A Note on ANOVA Results

To Use inference(): You won’t use aov() at all; instead…

inference(y = price, x = Neighborhood, data = ames_small,
          statistic = "mean", type = "ht", method = "theoretical",
          show_eda_plot = FALSE, show_inf_plot = FALSE)

Response variable: numerical
Explanatory variable: categorical (4 levels) 
n_CollgCr = 267, y_bar_CollgCr = 201803.4345, s_CollgCr = 54187.8437
n_Edwards = 194, y_bar_Edwards = 130843.3814, s_Edwards = 48030.405
n_NAmes = 443, y_bar_NAmes = 145097.3499, s_NAmes = 31882.7072
n_OldTown = 239, y_bar_OldTown = 123991.8912, s_OldTown = 44327.1045

ANOVA:
               df           Sum_Sq          Mean_Sq        F  p_value
Neighborhood    3 957415808260.877 319138602753.626 169.6027 < 0.0001
Residuals    1139 2143237728179.31  1881683694.6263                  
Total        1142 3100653536440.19                                   

Pairwise tests - t tests with pooled SD:
# A tibble: 6 × 3
  group1  group2   p.value
  <chr>   <chr>      <dbl>
1 Edwards CollgCr 5.91e-60
2 NAmes   CollgCr 3.48e-57
3 NAmes   Edwards 1.42e- 4
4 OldTown CollgCr 1.96e-77
5 OldTown Edwards 1.02e- 1
6 OldTown NAmes   1.82e- 9

Visual Confirmation

While a graphic alone cannot be used to conduct statistical inference, it can be used to confirm what we see numerically in a statistical test.

What Still Remains of Inference?

Inference On...	"Test" Name
One Binary Categorical Variable	One Sample z
Association Between Two Binary Categorical Variables	Two Sample z
One MultiClass Categorical Variable	Chi-Squared GOF
Associations Between Two MultiClass Categorical Variables	Chi-Squared Independence
One Numerical Variable	One Sample t
Association Between a Numerical Variable and a Binary Categorical Variable	Two Sample t
Association Between a Numerical Variable and a MultiClass Categorical Variable	ANOVA
Association Between a Numerical Variable and a Single Other Numerical Variable	?
Association Between a Numerical Variable and Many Other Variables	?
Association Between a Categorical Variable and Many Other Variables	✘ (MAT434)

The only remaining inference tasks for us to explore are those involving associations between two numerical variables (simple linear regression) and involving associations between a numerical variable and multiple other variables (multiple linear regression)

Aside: Linear Functions

Perhaps you remember the equation of a straight line from algebra: $y = mx + b$

$y$ and $x$ are numeric variables, where $x$ is often called the independent variable and $y$ is called the dependent variable
$m$ is the slope of the line – that is, the change in $y$ corresponding to a one-unit increase in $x$
$b$ is the intercept of the line – that is, the value of $y$ when $x = 0$

We can extend the notion of a linear function to include more than just one independent variable $x$

If $x_1,~x_2,~\cdots,~x_k$ are all independent variables, then the equation $y = b + m_1 x_1 + m_2 x_2 + \cdots + m_k x_k$ is an extension of a linear function to multiple dimensions

$m_i$ is the slope with respect to $x_i$ – that is, the change in $y$ corresponding to a one-unit increase in $x_i$ (holding all other $x_j$ constant)
$b$ is the intercept – that is, the value of $y$ if $x_i = 0$ for all $i$

Linear Regression

In simple linear regression, we have a numeric outcome variable of interest ($y$) and a numeric predictor variable $x$

Due to the random fluctuations in observed values of $y$ and $x$, a straight line will not pass through all of the observed $x,~y$-pairs but a straight line may capture the general trend between observed values of $x$ and corresponding observed values of $y$

Simple Linear Regression: We can describe the relationship above by the equation $\mathbb{E}\left[y\right] = \beta_0 + \beta_1\cdot x$

$\beta_0$ is the intercept – the expected value of $y$ when $x = 0$
$\beta_1$ is the slope – the expected change in $y$ corresponding to a unit increase in $x$

Multiple Linear Regression: We can extend the relationship above, accommodating multiple independent and numeric predictor variables$^{**}$, by the equation $\mathbb{E}\left[y\right] = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k$

$\beta_0$ is the intercept – the expected value of $y$ when $x_i = 0$ for all $i$
$\beta_1$ is the slope – the expected change in $y$ corresponding to a unit increase in $x_i$, holding all other $x_j$ constant

Completed Example: Simple Linear Regression

Disclaimer: There is much to learn about linear regression and we’ll just scratch the surface here. The MAT300 (Regression Analysis) course spends over half a semester on linear regression models so check it out if you are interested!

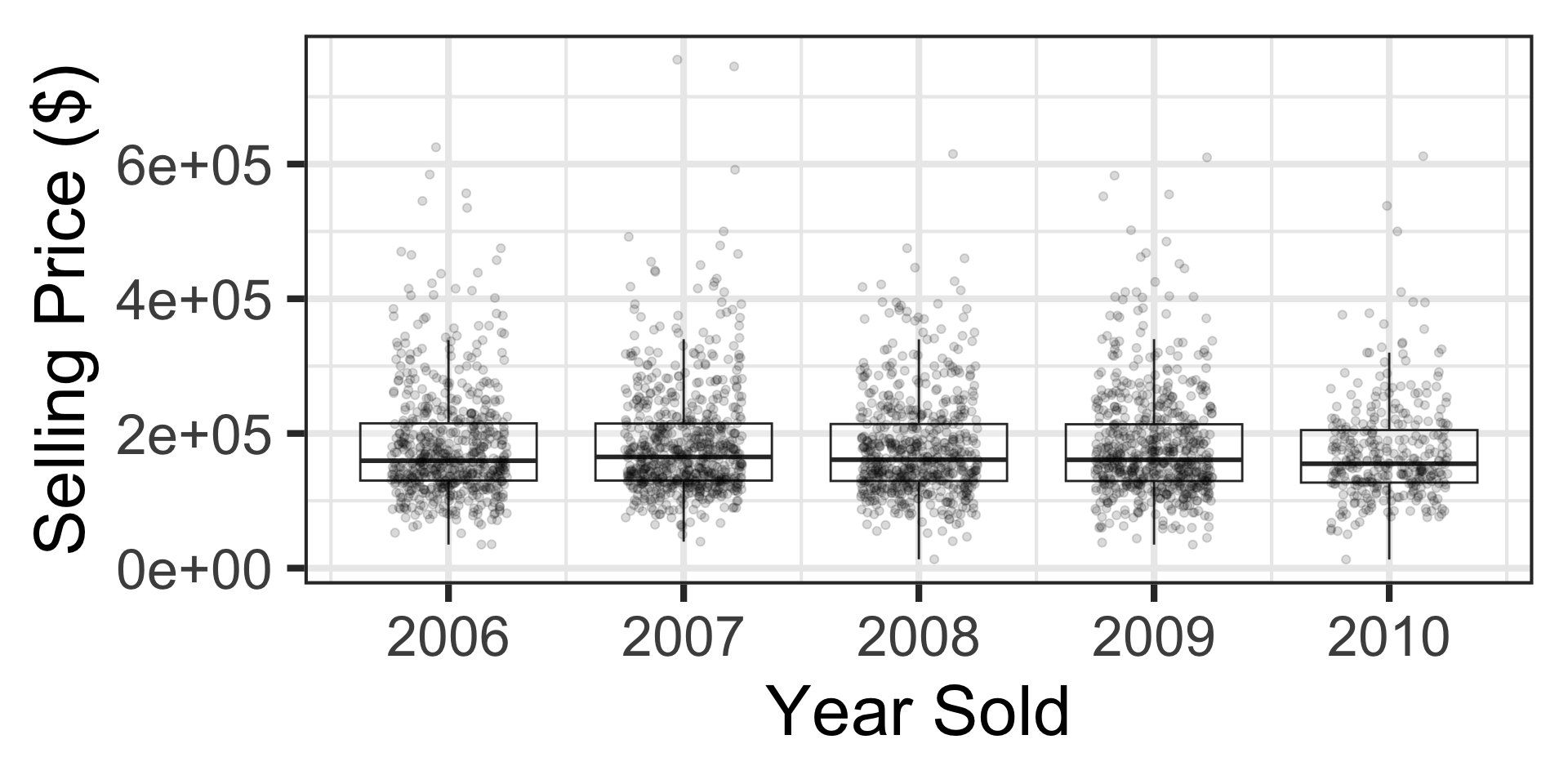
Inferential Question: Is there evidence to suggest that the average selling price for a home in Ames, IA changed from one year to the next during the 2006 - 2010 time period?

Note that selling price (price) and year sold (Yr.Sold) are both numeric variables, so linear regression is the tool we’ll need.

lr_mod <- lm(price ~ Yr.Sold, 
             data = ames)
lr_mod %>%
  tidy()

term	estimate	std.error	statistic	p.value
(Intercept)	3904860.382	2250330.229	1.735239	0.08280373
Yr.Sold	-1854.807	1120.799	-1.654897	0.09805253

Completed Example: Simple Linear Regression

Inferential Question: Is there evidence to suggest that the average selling price for a home in Ames, IA changed from one year to the next during the 2006 - 2010 time period?

term	estimate	std.error	statistic	p.value
(Intercept)	3904860.382	2250330.229	1.735239	0.08280373
Yr.Sold	-1854.807	1120.799	-1.654897	0.09805253

The Yr.Sold variable is statistically significant at the $\alpha = 0.10$ level of significance but not at the $\alpha = 0.05$ level of significance.

The fitted regression model suggests that: $\mathbb{E}\left[\text{price}\right] = 3904860 - 1854.81\cdot\text{Year}$

Notice that this model is suggesting that selling prices of homes in Ames, IA got cheaper over the 2006 to 2010 time period – likely a result of the subprime mortgage crisis.

Completed Example: Multiple Linear Regression

Inferential Question: Is there evidence to suggest that selling prices of homes in Ames, IA are associated with the living area (area), lot area (Lot.Area), lot frontage (Lot.Frontage), overall condition (Overall.Cond), year built (Year.Built), finished basement size (BsmtFin.SF.1), total rooms above ground (TotRms.AbvGrd), Fireplaces, Garage.Area, and the year sold (Yr.Sold)?

In this scenario, we are making use of lots of predictors but linear regression is still the tool for us to use!

Completed Example: Multiple Linear Regression

mlr_mod <- lm(price ~ area + Lot.Area + Lot.Frontage + Overall.Cond + Year.Built + BsmtFin.SF.1 + TotRms.AbvGrd + Yr.Sold + Fireplaces + Garage.Area, 
              data = ames)
mlr_mod %>%
  tidy() %>%
  gt()

term	estimate	std.error	statistic	p.value
(Intercept)	-2.943430e+05	1.282270e+06	-0.2295484	8.184620e-01
area	7.732128e+01	3.310836e+00	23.3540089	5.515168e-109
Lot.Area	5.481738e-01	1.551690e-01	3.5327530	4.189325e-04
Lot.Frontage	2.095404e+01	4.418357e+01	0.4742496	6.353646e-01
Overall.Cond	8.835328e+03	8.400642e+02	10.5174437	2.494798e-25
Year.Built	9.082560e+02	3.379981e+01	26.8716332	1.836704e-139
BsmtFin.SF.1	2.610161e+01	2.036448e+00	12.8172200	1.940931e-36
TotRms.AbvGrd	-1.550211e+03	9.457441e+02	-1.6391437	1.013129e-01
Yr.Sold	-7.619441e+02	6.376780e+02	-1.1948728	2.322535e-01
Fireplaces	1.367370e+04	1.547053e+03	8.8385471	1.822937e-18
Garage.Area	7.366734e+01	5.031763e+00	14.6404609	1.414082e-46

Notice that the $p$-values on several variables are higher than the $\alpha = 0.05$ level of significance

Completed Example: Multiple Linear Regression

term	estimate	std.error	statistic	p.value
(Intercept)	-2.943430e+05	1.282270e+06	-0.2295484	8.184620e-01
area	7.732128e+01	3.310836e+00	23.3540089	5.515168e-109
Lot.Area	5.481738e-01	1.551690e-01	3.5327530	4.189325e-04
Lot.Frontage	2.095404e+01	4.418357e+01	0.4742496	6.353646e-01
Overall.Cond	8.835328e+03	8.400642e+02	10.5174437	2.494798e-25
Year.Built	9.082560e+02	3.379981e+01	26.8716332	1.836704e-139
BsmtFin.SF.1	2.610161e+01	2.036448e+00	12.8172200	1.940931e-36
TotRms.AbvGrd	-1.550211e+03	9.457441e+02	-1.6391437	1.013129e-01
Yr.Sold	-7.619441e+02	6.376780e+02	-1.1948728	2.322535e-01
Fireplaces	1.367370e+04	1.547053e+03	8.8385471	1.822937e-18
Garage.Area	7.366734e+01	5.031763e+00	14.6404609	1.414082e-46

The $p$-values on Lot.Frontage, TotRms.AbvGrd, and Yr.Sold indicate that these predictors are not statistically significant – they are candidates for removal from the model

We’ll remove one predictor at a time, starting with Lot.Frontage since it has the largest $p$-value

Completed Example: Multiple Linear Regression

mlr_mod <- lm(price ~ area + Lot.Area + Overall.Cond + Year.Built + BsmtFin.SF.1 + TotRms.AbvGrd + Yr.Sold + Fireplaces + Garage.Area, 
              data = ames)
mlr_mod %>%
  tidy() %>%
  gt()

term	estimate	std.error	statistic	p.value
(Intercept)	3.109442e+05	1.138331e+06	0.273158	7.847511e-01
area	7.659370e+01	2.912533e+00	26.297966	5.716916e-137
Lot.Area	3.664148e-01	1.012082e-01	3.620407	2.991427e-04
Overall.Cond	8.465028e+03	7.241791e+02	11.689137	6.990825e-31
Year.Built	8.924039e+02	3.060811e+01	29.155801	3.130510e-164
BsmtFin.SF.1	2.627140e+01	1.821213e+00	14.425222	1.283976e-45
TotRms.AbvGrd	-1.560141e+03	8.291916e+02	-1.881521	6.000057e-02
Yr.Sold	-1.044427e+03	5.659507e+02	-1.845438	6.507512e-02
Fireplaces	1.238890e+04	1.341245e+03	9.236871	4.747040e-20
Garage.Area	6.964701e+01	4.463353e+00	15.604190	8.738445e-53

TotRms.AbvGrd and Yr.Sold are still not statistically significant, we’ll remove Yr.Sold this time since it has the highest $p$-value

Completed Example: Multiple Linear Regression

mlr_mod <- lm(price ~ area + Lot.Area + Overall.Cond + Year.Built + BsmtFin.SF.1 + TotRms.AbvGrd + Fireplaces + Garage.Area, 
              data = ames)
mlr_mod %>%
  tidy() %>%
  gt()

term	estimate	std.error	statistic	p.value
(Intercept)	-1.786725e+06	6.133779e+04	-29.129265	5.617300e-164
area	7.660925e+01	2.913721e+00	26.292583	6.343693e-137
Lot.Area	3.702735e-01	1.012283e-01	3.657806	2.588789e-04
Overall.Cond	8.432137e+03	7.242580e+02	11.642449	1.180154e-30
Year.Built	8.927757e+02	3.062005e+01	29.156568	3.030702e-164
BsmtFin.SF.1	2.617136e+01	1.821156e+00	14.370739	2.677055e-45
TotRms.AbvGrd	-1.543855e+03	8.294862e+02	-1.861219	6.281373e-02
Fireplaces	1.239109e+04	1.341797e+03	9.234697	4.840625e-20
Garage.Area	6.965581e+01	4.465189e+00	15.599743	9.304027e-53

Now we’ll remove TotRms.AbvGrd since it is still not statistically significant

Completed Example: Multiple Linear Regression

mlr_mod <- lm(price ~ area + Lot.Area + Overall.Cond + Year.Built + BsmtFin.SF.1 + Fireplaces + Garage.Area, 
              data = ames)
mlr_mod %>%
  tidy() %>%
  gt()

term	estimate	std.error	statistic	p.value
(Intercept)	-1.800359e+06	6.092452e+04	-29.550639	3.903929e-168
area	7.240431e+01	1.840782e+00	39.333445	6.574109e-272
Lot.Area	3.687902e-01	1.012678e-01	3.641731	2.755167e-04
Overall.Cond	8.477005e+03	7.241620e+02	11.705950	5.779576e-31
Year.Built	8.974738e+02	3.052870e+01	29.397705	1.264713e-166
BsmtFin.SF.1	2.669187e+01	1.800314e+00	14.826235	5.287639e-48
Fireplaces	1.258046e+04	1.338498e+03	9.398936	1.076905e-20
Garage.Area	6.997559e+01	4.463765e+00	15.676361	3.061261e-53

All of the remaining model terms are statistically significant, so we’ve arrived at our final model

Completed Example: Multiple Linear Regression

term	estimate	std.error	statistic	p.value
(Intercept)	-1.800359e+06	6.092452e+04	-29.550639	3.903929e-168
area	7.240431e+01	1.840782e+00	39.333445	6.574109e-272
Lot.Area	3.687902e-01	1.012678e-01	3.641731	2.755167e-04
Overall.Cond	8.477005e+03	7.241620e+02	11.705950	5.779576e-31
Year.Built	8.974738e+02	3.052870e+01	29.397705	1.264713e-166
BsmtFin.SF.1	2.669187e+01	1.800314e+00	14.826235	5.287639e-48
Fireplaces	1.258046e+04	1.338498e+03	9.398936	1.076905e-20
Garage.Area	6.997559e+01	4.463765e+00	15.676361	3.061261e-53

The estimated model form is

\[\begin{align} \mathbb{E}\left[\text{price}\right] = &-1800539 + 72.4\text{area} + 0.37\text{LotArea} + 8477\text{OverallCond} + 897.47\text{YrBuilt}~+\\ &~26.69\text{BsmtFinSF} + 12580.46\text{Fireplaces} + 69.98\text{GarageArea} \end{align}\]

There are lots of inferences we can draw from this model – for example, holding all other predictors constant, each additional fireplace is associated with a higher selling price by about $12,580.46

Summary and Closing

Inference On...	"Test" Name
One Binary Categorical Variable	One Sample z
Association Between Two Binary Categorical Variables	Two Sample z
One MultiClass Categorical Variable	Chi-Squared GOF
Associations Between Two MultiClass Categorical Variables	Chi-Squared Independence
One Numerical Variable	One Sample t
Association Between a Numerical Variable and a Binary Categorical Variable	Two Sample t
Association Between a Numerical Variable and a MultiClass Categorical Variable	ANOVA
Association Between a Numerical Variable and a Single Other Numerical Variable	Simple Linear Regression (More in MAT300)
Association Between a Numerical Variable and Many Other Variables	Multiple Linear Regression (More in MAT300)
Association Between a Categorical Variable and Many Other Variables	✘ (MAT434)

We’ve covered lots of ground in this course – you leave MAT241 with an ability to conduct statistical inference in many contexts

There’s still more to discover though, and I hope some of your will join me in future semesters to take MAT300 and MAT434

Summary and Closing

via GIPHY

Analysis of Variance (ANOVA) and Linear Regression

The Highlights

What’s Left for Inference?

The ames Home Sales Data

Analysis of Variance (ANOVA)

Analysis of Variance (ANOVA)

Analysis of Variance (ANOVA)

Analysis of Variance (ANOVA)

Intuition for ANOVA

Mechanics of ANOVA

Mechanics of ANOVA

Completed Example: Home Sales by Neighborhood

A Note on ANOVA Results

A Note on ANOVA Results

A Note on ANOVA Results

Visual Confirmation

What Still Remains of Inference?

Aside: Linear Functions

Linear Regression

Completed Example: Simple Linear Regression

Completed Example: Simple Linear Regression

Completed Example: Multiple Linear Regression

Completed Example: Multiple Linear Regression

Completed Example: Multiple Linear Regression

Completed Example: Multiple Linear Regression

Completed Example: Multiple Linear Regression

Completed Example: Multiple Linear Regression

Completed Example: Multiple Linear Regression

Summary and Closing

Summary and Closing

The `ames` Home Sales Data