Introduction to K Nearest Neighbors (KNN)

Purpose: In this notebook we introduce the \(k\) nearest neighbors classifier. In particular, we note that

the \(k\) in the name of the classifier indicates the number of voting neighbors when a prediction is made.
nearest neighbors is a distance-based model.
- Numerical predictors should be scaled in order to use this class of model.
- Categorical predictors are not supported by nearest neighbor models without significant assumptions made regarding relationships between their levels.
- Nearest neighbor models suffer greatly from the curse of dimensionality.

The Big Idea

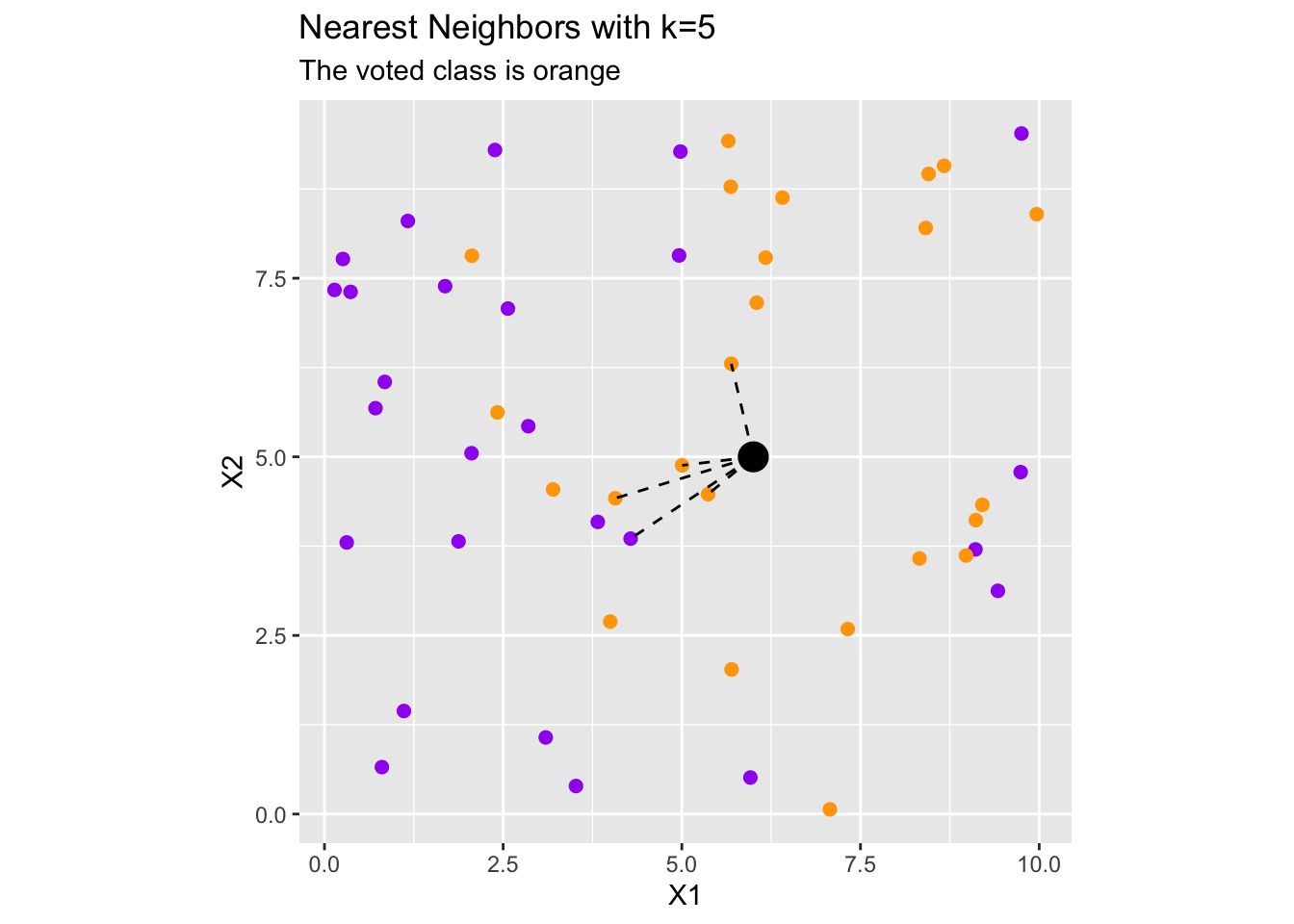
A nearest neighbor model assumes that observations are most like those nearest to them. The nearest neighbor model makes predictions on a new observation in the following way:

Identify the \(k\) observations which are closest to the new observation. (Note: It is possible to use a variety of distance metrics, not just the Euclidean metric.)
Allow those \(k\) “nearest neighbors” to vote on the response for the new observation.

The following visual may be helpful.

About KNN

Given the two stage process, you might note that a nearest neighbor model isn’t actually trained. The “locations” and responses for the training data are simply stored, and when a prediction is to be made, the algorithm is run. This has several implications.

The nearest neighbor approach is not a model, it is really an algorithm to obtain predictions.
The nearest neighbor approach is expensive in terms of memory requirements because the entire “training” set must be stored in perpetuity.
The nearest neighbor approach is expensive in terms of compute time because the algorithm must be run in full every time a new prediction is to be made.
The nearest neighbors algorithm is non-parametric and no functional form is estimated.
- This means that nearest neighbors does not result in an interpretable model like linear regression, logistic regression, decision trees, or others do.

Where nearest neighbor approaches have the drawbacks cited above, they do have some significant advantages. In particular, they can approximate very complex decision boundaries. We can also tune the parameter \(k\) in order to obtain an appropriately flexible boundary.

Regression and Classification

It is worth noting that \(k\) nearest neighbors can be used in both the classification and regression settings.

For classification, each neighbor provides a vote for the class of the new observation and the plurality wins.
For regression, the value of the response for each of the nearest neighbors are averaged to obtain the predicted response for the new observation.

How to Implement in `{tidymodels}`

A KNN classifier is a model class (that is, a model specification). We define our intention to build a KNN classifier using

knn_clf_spec <- nearest_neighbor() %>%
  set_engine("kknn") %>%
  set_mode("classification")

K Nearest Neighbors can be used for both regression and classification. For this reason, the line to set_mode() is required when declaring the model specification. The line to set_engine() above is unnecessary since kknn is the default engine. There are other available engines though.

Hyperparameters and Other Extras

Like other model classes, nearest neighbors have tunable hyperparameters. They are

neighbors, which determines the number of voting neighbors to determine the model’s ultimate prediction on a new observation.
- Remember, the fewer voting neighbors, the more flexible the model is.
weight_func determines how we’ll compute distances between observations. More than just Euclidean distance ("rectangular") are available.

You can see the full {parsnip} documentation for nearest_neighbor() here.

Summary

In this notebook we learned a bit about the \(k\) nearest neighbors algorithm. In particular, we saw that this is a distance-based algorithm which can be used for either regression or classification. We also saw that it is a non-parametric method which does not result in a model and cannot be interpreted. The algorithm is run every time a new prediction is to be made, making nearest neighbors an expensive algorithm in terms of both space and time. While nearest neighbors has its drawbacks it is a powerful technique which can fit very complex decision boundaries in the classification setting and can approximate complex functions well in the regression setting. Nearest neighbors also makes no distribution assumptions about the underlying data – only that observations are most similar to those around them.